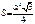Среднее арифметическое, геометрическое
Среднее арифметическое: 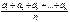
Среднее геометрическое: 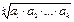
Уравнение движения
Пусть 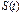 - уравнение движения материальной точки, где S – путь, t – время движения.
- уравнение движения материальной точки, где S – путь, t – время движения.
Тогда: 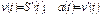 ,
,
где 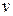 – скорость,
– скорость, 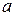 - ускорение.
- ускорение.
Определенный интеграл
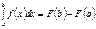
Первообразная элементарных функций
| № | f(x) | F(x) | № | f(x) | F(x) | ||
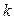 | 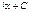 | 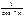 | 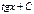 | ||||
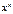 | 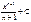 | ||||||
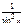 | 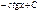 | ||||||
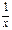 | 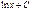 | ||||||
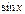 | 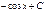 | 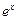 | 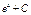 | ||||
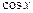 | 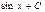 | 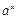 | 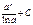 |
Правила вычисления первообразной функции
Определение: Функция F(x) называется первообразной для функции f(x), если 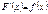 .
.
| Функция | Первообразная |
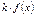 | 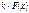 |
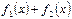 | 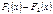 |
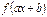 | 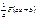 |
Правила вычисления производной функции
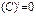 | 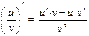 |
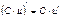 | |
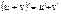 |  Сложная функция: Сложная функция: 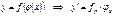 |
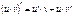 |
Производные элементарных функций
| № | Функция | Производная | № | Функция | Производная | ||
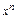 | 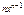 | 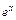 | 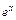 | ||||
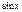 | 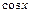 | 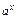 | 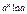 | ||||
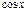 | 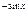 | ||||||
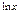 | 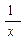 | ||||||
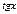 | 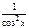 | ||||||
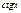 | 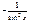 | 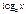 | 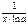 |
Равносильные уравнения:
| Исходное уравнение | Равносильное уравнение (система) | |
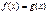 | Û | 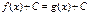 |
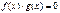 | Û | 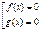 |
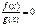 | Û | 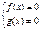 |
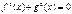 | Û | 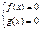 |
Числовые множества:
| Натуральные числа | N = { 1; 2; 3; 4; . .} |
| Целые числа | Z = N È { 0; -1; -2; -3; …} |
| Рациональные числа | Q = Z È 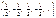 |
| Действительные числа | R = Q È 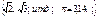 |
Тригонометрия
Основные триг. формулы
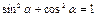 Þ
Þ 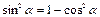
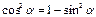
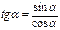
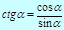 Þ
Þ 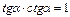
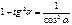
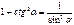
Формулы суммы функций
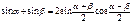
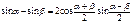
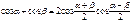
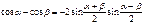
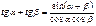
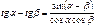
Формулы суммы аргументов:
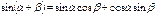
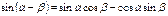
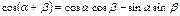
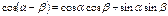
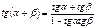
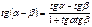
Формулы произведения функций
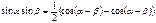
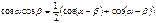
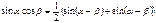
Формулы половинного аргумента
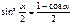
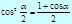
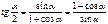
Формулы двойного аргумента
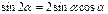
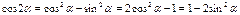
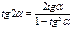
Формула дополнительного угла
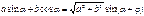 где
где
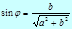
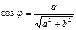
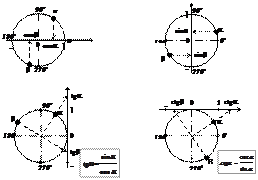 Определение тригонометрических функций
Определение тригонометрических функций
Универсальная подстановка
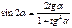
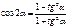
Свойства тригонометрических функций
| Функция | Свойства | |||
| Область определения | Множество значений | Четность-нечетность | Период | |
| cosx | 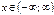 | 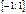 | cos(-x)= cosx | 2p |
| sinx | 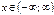 | 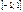 | sin(-x)= -sinx | 2p |
| tgx | 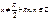 | 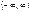 | tg(-x)= -tgx | p |
| ctgx | 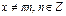 | 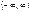 | ctg(-x)= -ctgx | p |
Тригонометрические уравнения
Косинус:
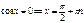
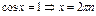
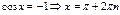
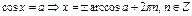
Уравнения с синусом
Частные формулы:
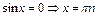
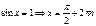
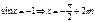
Общая формула:
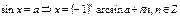
Уравнения с тангенсом и котангенсом
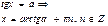
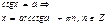
Формулы обратных триг функций
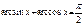
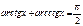
| Если 0 < x £ 1, то arccos(-x) = p - arccosx arcsin(-x) = - arcsinx | Если x > 0 , то arctg(-x) = - arctgx arcctg(-x) = p - arcctgx |
Обратные триг функции
| Функция | Свойства | ||
| Область определения | Множество значений | ||
| arccosx | 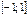 | [0; p] | |
| arcsinx | 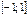 | [-p/2; p/2] | |
| arctgx | 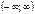 | (-p/2; p/2) | |
| arcctgx | 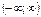 | (0; p) | |
Геометрия
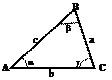 Теорема косинусов, синусов
Теорема косинусов, синусов
Теорема косинусов:
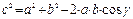
Теорема синусов:
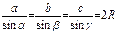
Площадь треугольника
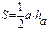
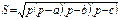
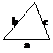 | 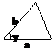 | ||||
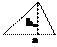 |
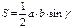
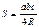
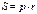
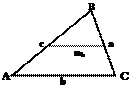 Средняя линия
Средняя линия
Средняя линия – отрезок, с соединяющий середины двух с сторон треугольника.
Средняя линия параллельна т третьей стороне и равна е её половине: 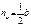
Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного
Равносторонний треугольник
треугольник, у которого все стороны равны.
v Все углы равны 600.
v Каждая из высот является одновременно биссектрисой и медианой.
v Центры описанной и вписанной окружностей совпадают.
v Радиусы окружностей: 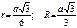
Площадь