Общая характеристика методов решения систем линейных уравнений

Методы решения систем линейных уравнений в основном делятся на две группы:

1. Точные методы - представляющие собой конечные алгоритмы для вычисления корней системы.

2. Итерационные методы - позволяющие получить корни системы уравнений с заданной точночтью путём бесконечных сходящихся процессов.

Введём следующие обозначения:

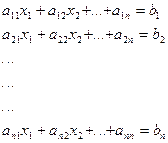
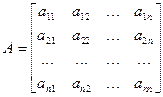- матрица коэффициентов

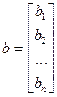- столбец свободных членов

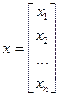- столбец неизвестных

Решение имеет место, если матрица 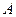- неособенная, то есть

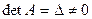
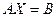
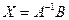- решение системы с помощью обратной матрицы

Сложность нахождения обратной матрицы для 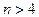заключается в большом времени нахождения .

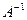Это обстоятельство обходится с помощью правила Крамера

,

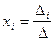где 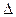- определитель матрицы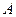

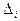- определитель матрицы, полученный из матрицы 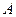путём замещения 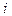-го столбца на столбец свободных членов .

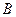Пример: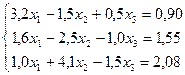

Прямой метод

,

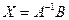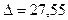
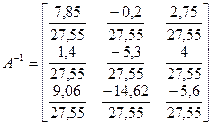
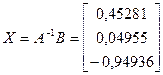
По правилу Крамера

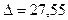
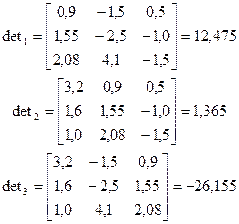
Метод Гаусса. Схема единственного деления

Наиболее распространённым приёмом решения системы линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных.

Рассмотрим для простоты систему линейных алгебраических уравнений 4-го порядка:

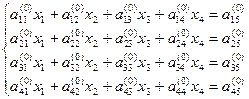
1. Выбираем ведущий элемент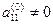

2. Поделив первое уравнение на 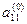, получаем

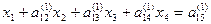, (2)

где , ,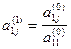

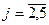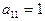
3. Исключаем переменную 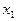из всех последующих уравнений, начиная со второго, путём вычитания уравнения 2, умноженного на коэффициент, стоящий при 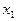в соответствующем уравнении. Получаем

,

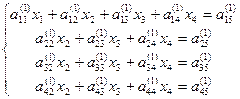где , ,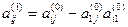

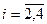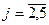
4. Выбираем ведущий элемент во втором уравнении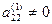

и так далее.

Если 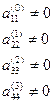, то получим систему

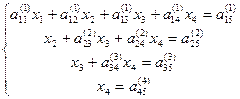, (3)

то есть матрица 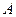имеет диагональный вид:

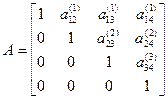
Из системы 3 отыскиваем 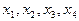следующим образом

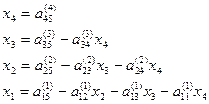, (4)

Процесс приведения матрицы к треугольному виду 3 называется прямым ходом, а нахождение корней по 4 обратным ходом.

Пример: прежний, но методом Гаусса. Приводит к системе уравнений:

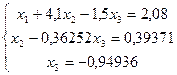- прямой ход

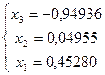- обратный ход

Существует схема единственного деления, которая используется при дирном счёте, но мы либо рассмотрим её на практике, либо вообще не будем рассматривать.

То есть в нашем курсе мы ориентируемся на вычислительную технику и все методы интересуют как алгоритмы.

Трудоёмкость метода Гаусса

1. Прямой ход

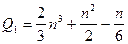
2. Обратный ход

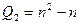
Общее число выполняемых арифметических действий

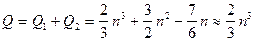
то есть для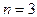

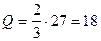
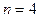
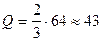
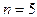
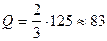
Предложенный метод Гаусса ориентирован на то, чтобы ведущие элементы не равнялись 0. А если на каком-то шаге возникает ситуация, что ведущий элемент равен 0, то тогда схема “формально” непригодна, хотя заданная система может иметь единственное решение.

Тогда применяют разновидность метод Гаусса -схема с выбором главного элемента: