Образец выполнения задания № 2. Задача.Дана функция
Задача.Дана функция 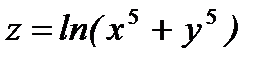 . Найдите ее градиент в точке
. Найдите ее градиент в точке 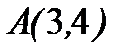 и производную линии
и производную линии 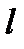 :
: 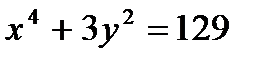 .
.
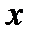 |
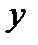 |
| -3 |
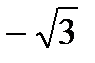 |
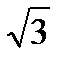 |
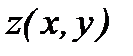 в произвольной точке
в произвольной точке 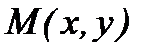 вычисляется по формуле
вычисляется по формуле 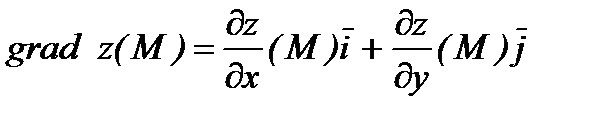 (1).
(1). Рис. 8
Найдем его.
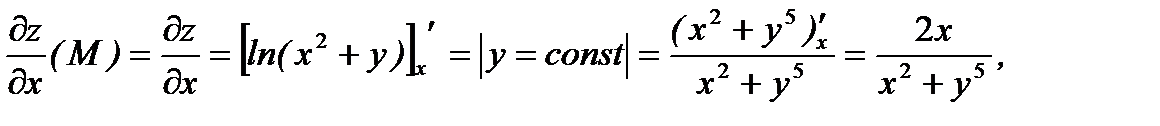
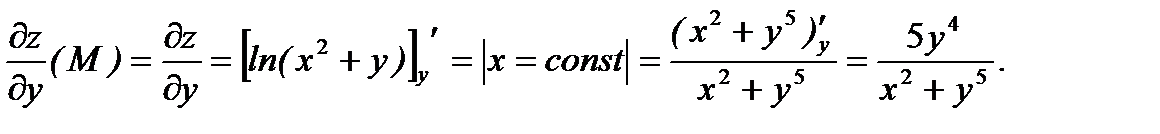
Найдем эти значения в точке  .
.
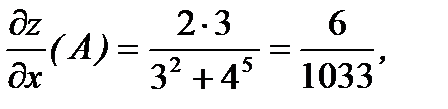
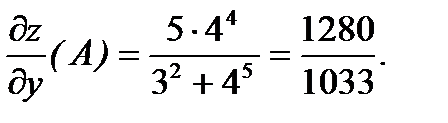
Отсюда получаем градиент в точке А по формуле (1).
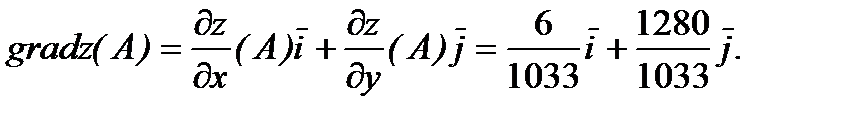
Производная функции 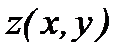 в точке А по направлению вектора
в точке А по направлению вектора 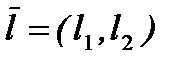 вычисляется по формуле
вычисляется по формуле 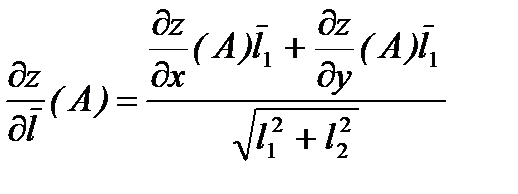 (2).
(2).
В данной задаче 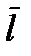 направлен по касательной к линии
направлен по касательной к линии 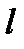 в точке А (это и означает, что мы ищем производную по направлению линии
в точке А (это и означает, что мы ищем производную по направлению линии 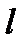 , см. рис. 7).
, см. рис. 7).
В общем случае, когда 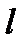 имеет уравнение
имеет уравнение 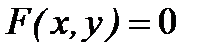 , координаты касательного вектора
, координаты касательного вектора 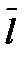 в произвольной точке вычисляются по формуле
в произвольной точке вычисляются по формуле
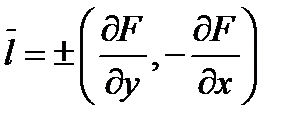
(знак 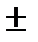 соответствует тому, что в точке А можно нарисовать два противоположно – направленных касательных вектора). В нашей задаче
соответствует тому, что в точке А можно нарисовать два противоположно – направленных касательных вектора). В нашей задаче 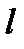 :
: 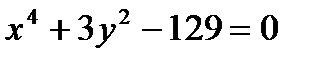 , поэтому
, поэтому
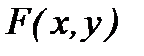
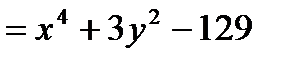 ,
,
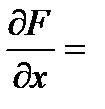
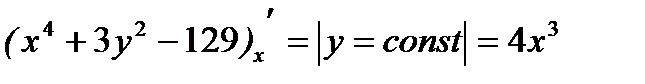 ,
, 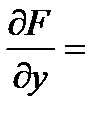
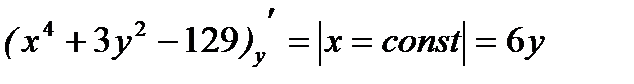 .
.
В точке А эти значения получаются такими 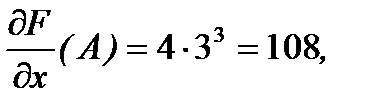
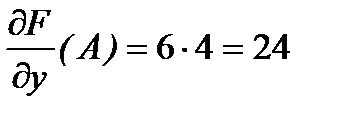 .
.
Отсюда 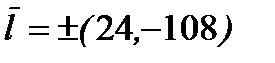 .
.
Давайте укоротим этот вектор в 12 раз; координаты остаются целыми 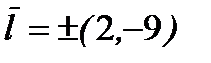 , но дальнейшие вычисления упростятся. По формуле (2) получаем
, но дальнейшие вычисления упростятся. По формуле (2) получаем
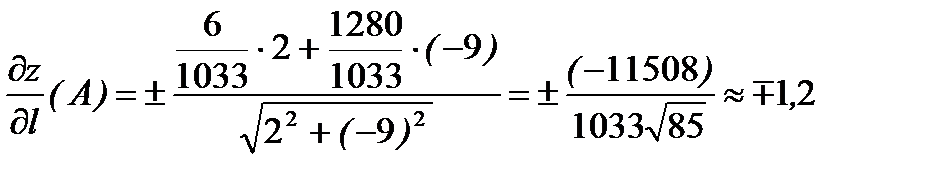 .
.
Если мы хотим найти производную в сторону возрастания координаты х, то должно быть 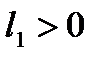 . В нашей задаче это получится, если у
. В нашей задаче это получится, если у 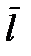 взять знак +, так как тогда
взять знак +, так как тогда 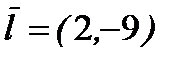 ,
, 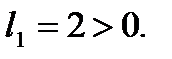 Выбрав таким образом верхний знак, получим
Выбрав таким образом верхний знак, получим 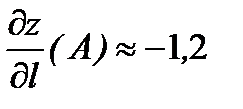 .
.
Образец выполнения задания № 3
Алгоритм исследования функции 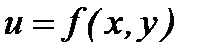 на экстремум.
на экстремум.
1) Проверить необходимое условие экстремума:
Найти частные производные первого порядка 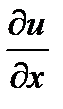 ,
, 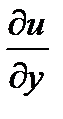 .
.
Решив систему уравнений 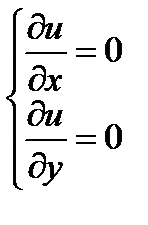 , найти точки возможного экстремума.
, найти точки возможного экстремума.
2) Проверить достаточные условия экстремума.
Найти частные производные второго порядка 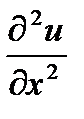 ,
, 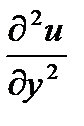 ,
, 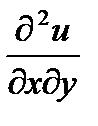 .
.
Составить матрицу 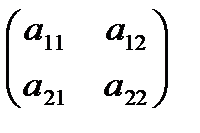 , где
, где 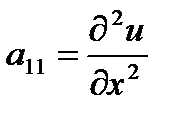 ,
, 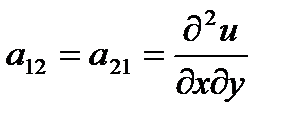 ,
, 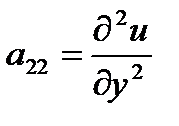 ,
,
и найти 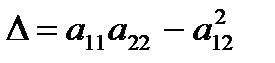 .
.
Вычислить  в точках возможного экстремума. Если
в точках возможного экстремума. Если 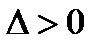 , то в данной точке функция имеет экстремум, а именно – максимум при
, то в данной точке функция имеет экстремум, а именно – максимум при 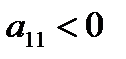 (или
(или 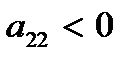 ) и минимум при
) и минимум при 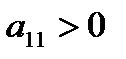 (или
(или 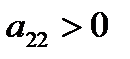 ); если
); если 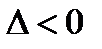 , то в данной точке экстремума нет; если
, то в данной точке экстремума нет; если 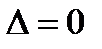 , то требуется дальнейшее исследование.
, то требуется дальнейшее исследование.
Образец выполнения задания № 4
Задача.Найдем экстремум функции 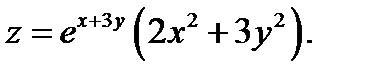
Решение.Найдем частные производные первого порядка:
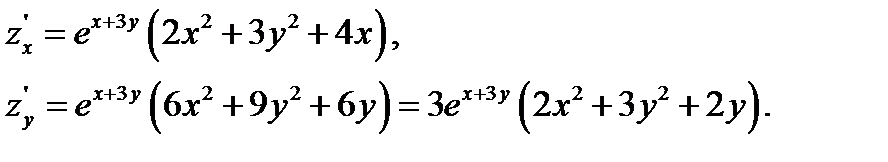 (1)
(1)
Решим систему уравнений:
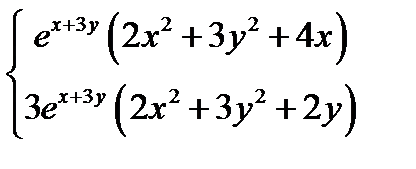 или
или 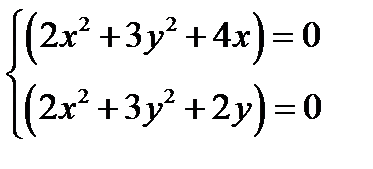
Из второго уравнения вычтем первое. Получим:
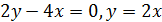 . (2)
. (2)
Подставим в первое уравнение: 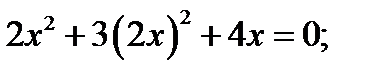
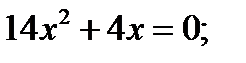
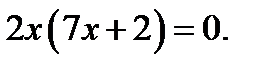 Отсюда
Отсюда 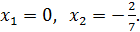 Подставим в (2). Будем иметь
Подставим в (2). Будем иметь 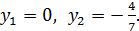 Значит,
Значит, 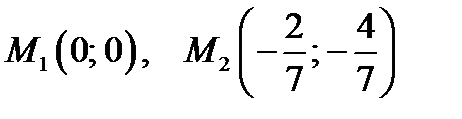 - стационарные точки, в которых возможен экстремум.
- стационарные точки, в которых возможен экстремум.
Из (1) найдем частные производные второго порядка:
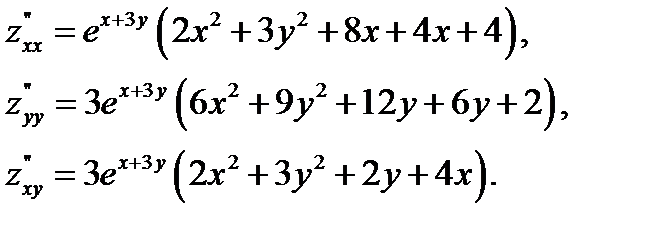
В точке 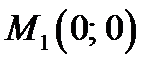 эти значения равны:
эти значения равны: 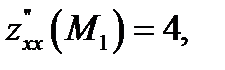
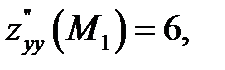
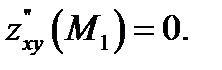 Тогда
Тогда 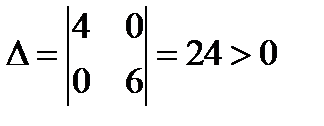 . Кроме того,
. Кроме того, 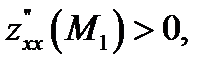 поэтому
поэтому 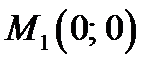 - точка минимума.
- точка минимума.
В точке 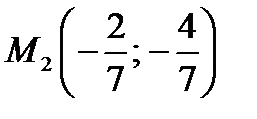 имеем
имеем 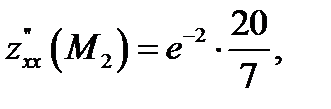
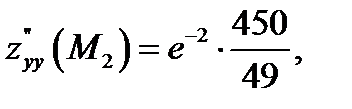
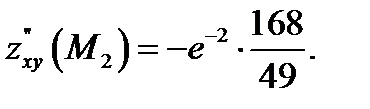
Тогда 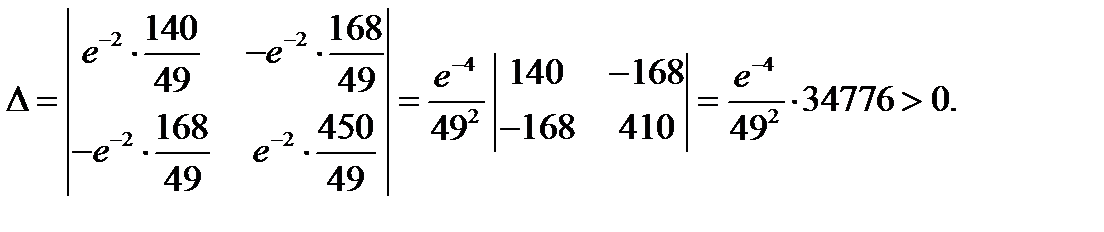 Кроме того
Кроме того 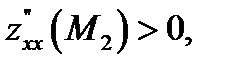 поэтому
поэтому 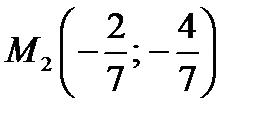 – точка минимума.
– точка минимума.
Образец выполнения задания № 5
Задача.Найти частные производные второго порядка и дифференциал функции 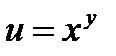 .
.
Решение: Сначала находим частные производные первого порядка 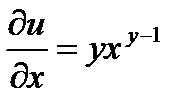 ,
, 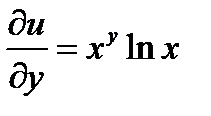 . Дифференциал функции равен
. Дифференциал функции равен 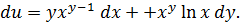 Затем вычисляем частные производные от частных производных первого порядка.
Затем вычисляем частные производные от частных производных первого порядка.
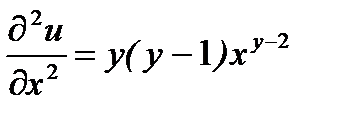 ,
, 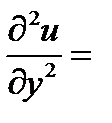
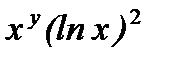 ,
,
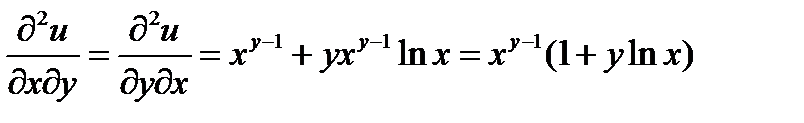 .
.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 3
Задание № 1
Требуется исследовать функцию методами дифференциального исчисления и начертить ее график. Для этого рекомендуется:
1. Определить, в каких интервалах функция существует и непрерывна. Найти точки разрыва функции, если они имеются.
2. Выяснить, не является ли функция четной или нечетной, т.е. не симметричен ли ее график относительно оси ординат или начала координат.
3. Найти точки пересечения графика функции с осями координат и интервалы, в которых функция сохраняет постоянный знак.
4. Определить вертикальные и невертикальные асимптоты графика функции.
5. Найти интервалы возрастания и убывания функции и точки экстремума.
6. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.
7. Наконец, построить график функции, используя все собранные данные (если окажется, что последних недостаточно для того, чтобы составить представление о ходе графика, нужно дополнительно найти несколько лежащих на нем точек).
1. 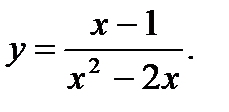 2.
2. 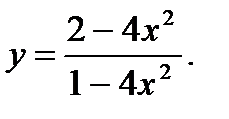
3. 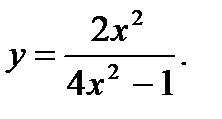 4.
4. 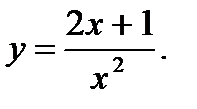
5. 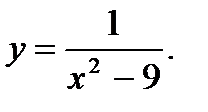 6.
6. 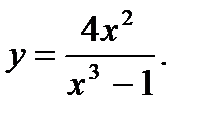
7. 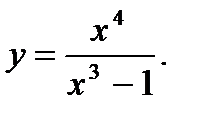 8.
8. 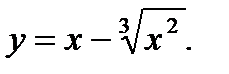
9. 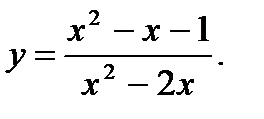 10.
10. 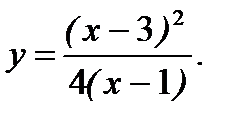
11. 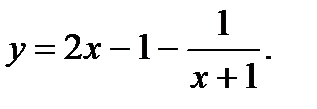 12.
12. 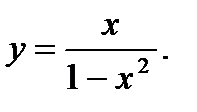
13. 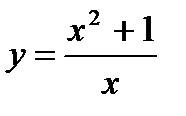 14.
14. 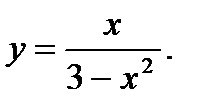
15. 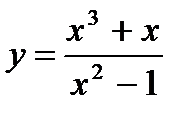 16.
16. 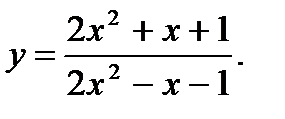
17. 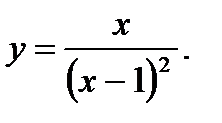 18.
18. 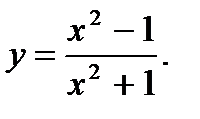
19. 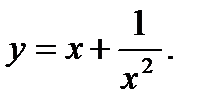
20. 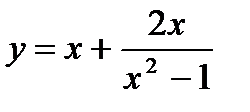
21. 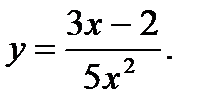
22. 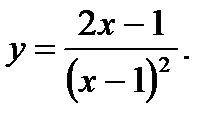
23. 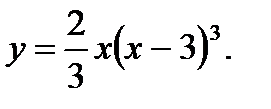 24.
24. 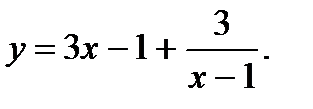
25. 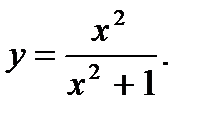 26.
26. 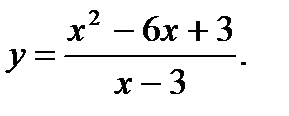
27. 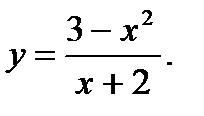 28.
28. 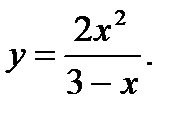
29. 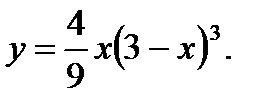 30.
30. 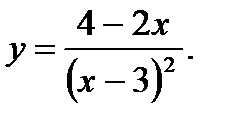
Задание № 2
Найти 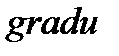 и производную от функции
и производную от функции 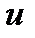 в точке
в точке 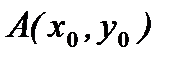 в направлении линии
в направлении линии 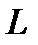 , в сторону возрастания координаты х, сделать чертеж.
, в сторону возрастания координаты х, сделать чертеж.
1. 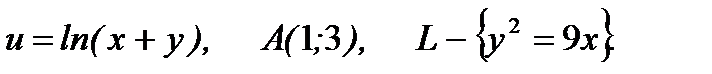
2. 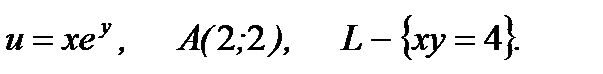
3. 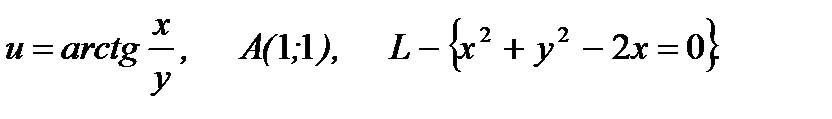
4. 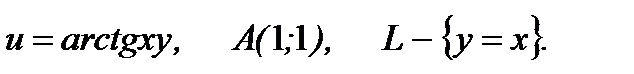
5. 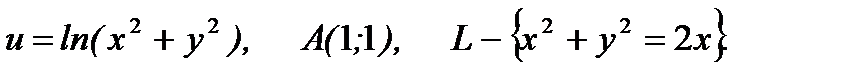
6. 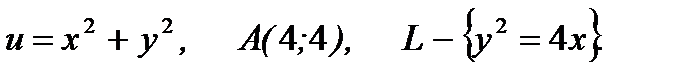
7. 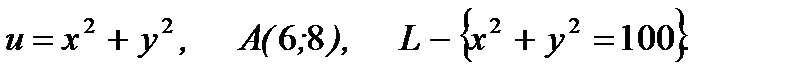
8. 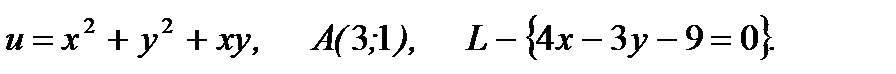
9. 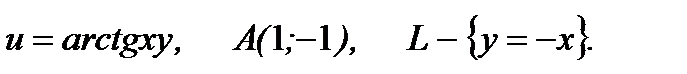
10. 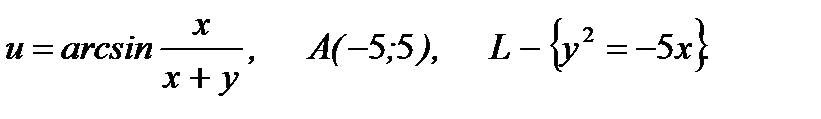
11. 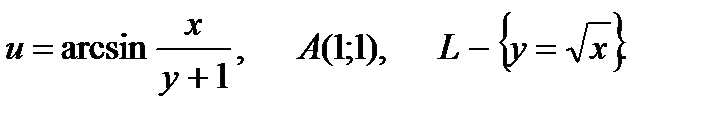
12. 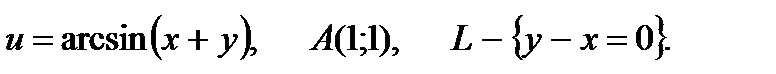
13. 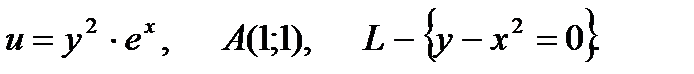
14. 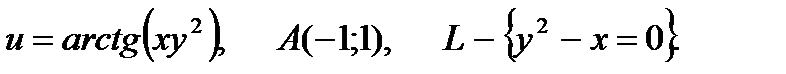
15. 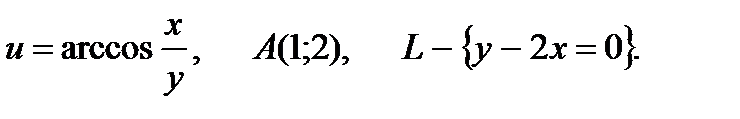
16. 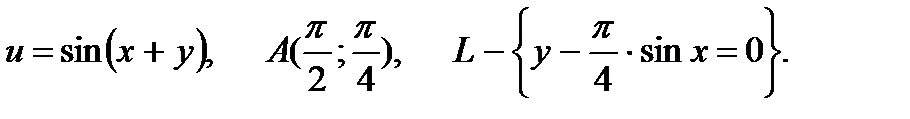
17. 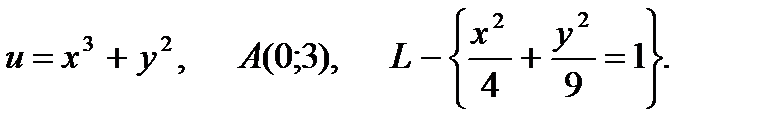
18. 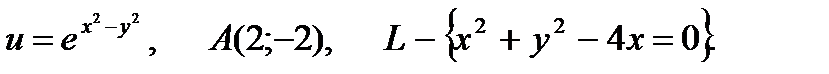
19. 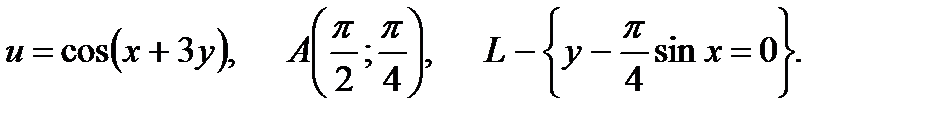
20. 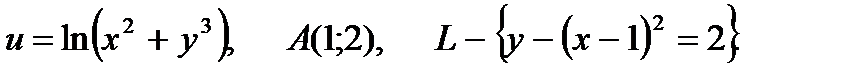
21. 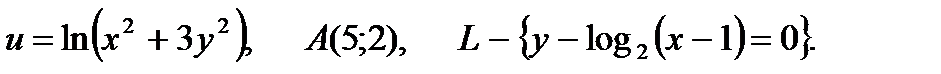
22. 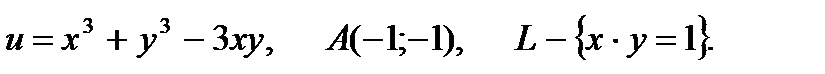
23. 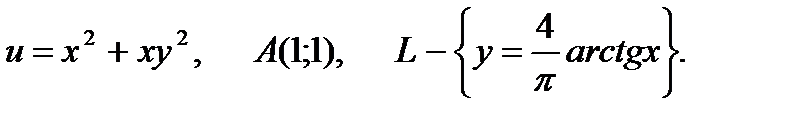
24. 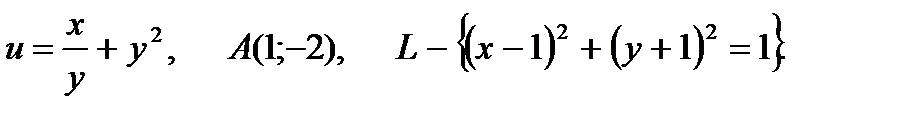
25. 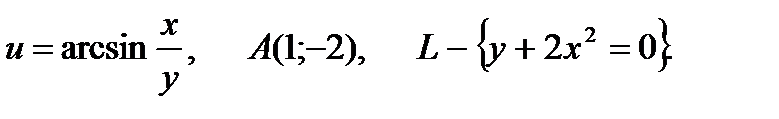
26. 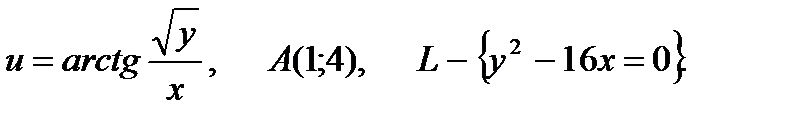
27. 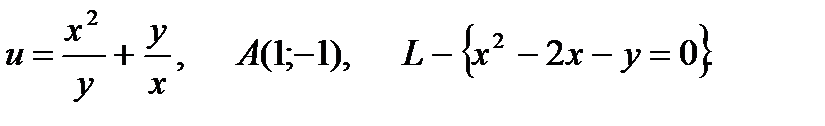
28. 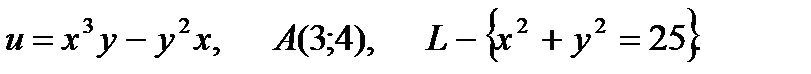
29. 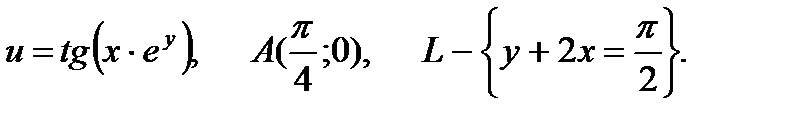
30. 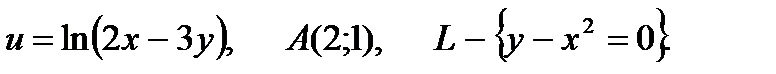
Задание № 3
Исследовать на экстремум.
1. 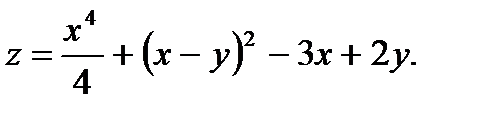
2. 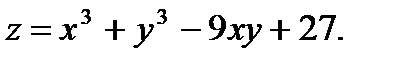
3. 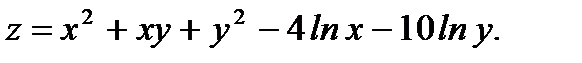
4. 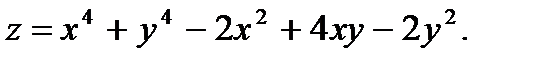
5. 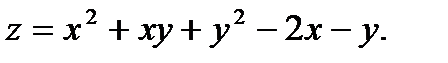
6. 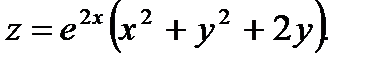
7. 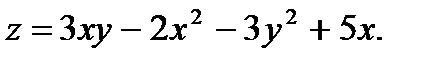
9. 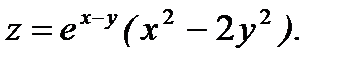
8. 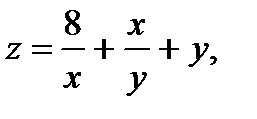
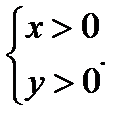
10. 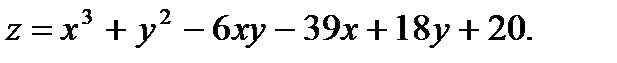
11. 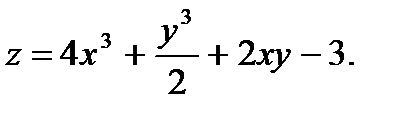
12. 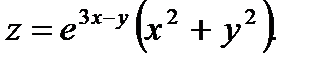
13. 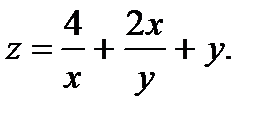
14. 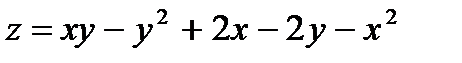
15. 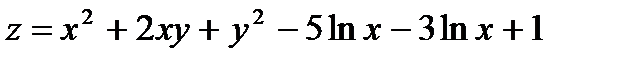
16. 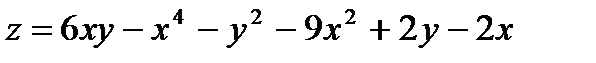
17. 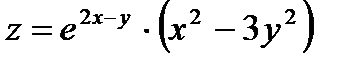
18. 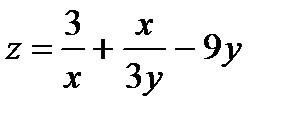
19. 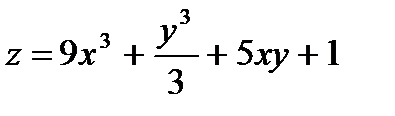
20. 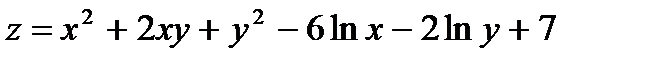
21. 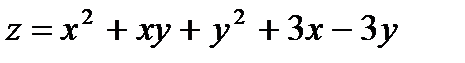
22. 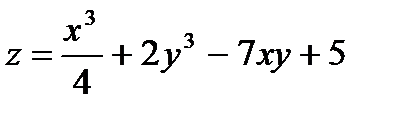
23. 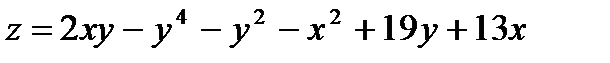
24. 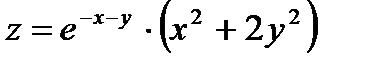
25. 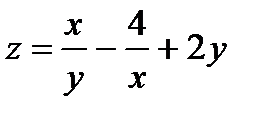
26. 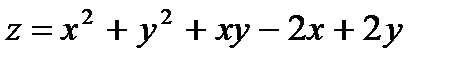
27. 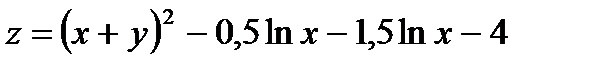
28. 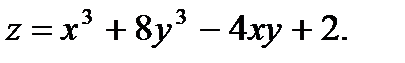
29. 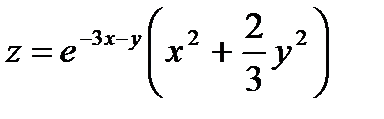
30. 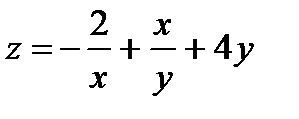
Задание № 4
Для заданной функции 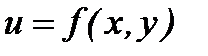 найти:
найти: 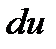 ,
, 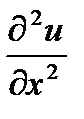 ,
, 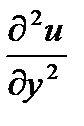 ,
, 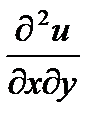 ,
, 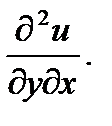
1. 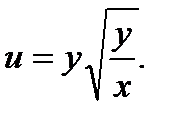
2. 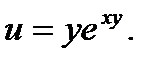
3. 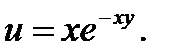
4. 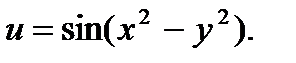
5. 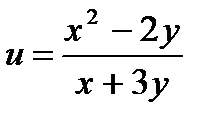
6. 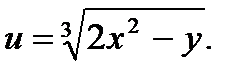 7.
7. 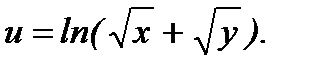
8. 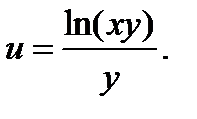
9. 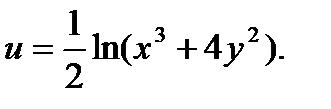
10. 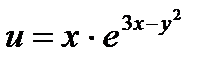
11. 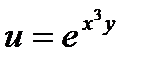
12. 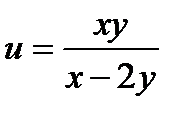
13. 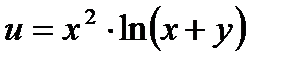
14. 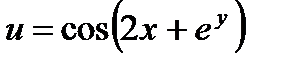
15. 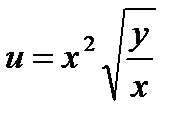
16. 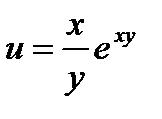
17. 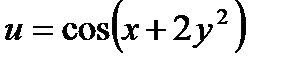 18.
18. 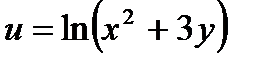
19. 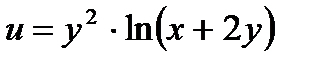
20. 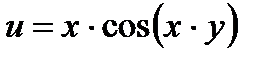
21. 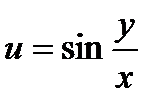
22. 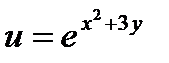
23. 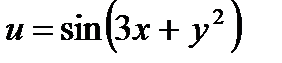 24.
24. 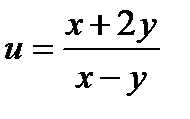
25. 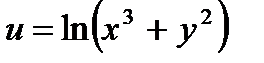
26. 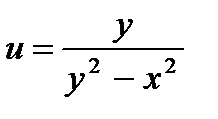 27.
27. 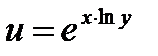
28. 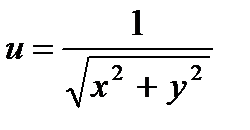
29. 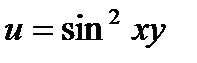 30.
30. 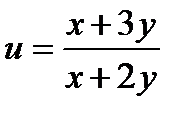
Содержание Курса «математика»
II СЕМЕСТР
