Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:

Билет 17
Индуктивное сопротивление. Сопротивление катушки или проводника переменному току, вызванное действием э. д. с. самоиндукции, называется индуктивным сопротивлением. Оно обозначается XL и измеряется в омах.
Следовательно, индуктивное сопротивление не зависит от материала, из которого изготовлен проводник (катушка), и от площади поперечного сечения проводника.
Закон Ома для цепи с индуктивностью
I = U / xL = U / (?L)
Так как среднее значение мощности в цепи с индуктивностью равно нулю, для характеристики процесса обмена энергией между источником и индуктивностью введено понятие реактивной мощности индуктивности:
QL = ULI
где UL — напряжение, приложенное к индуктивности L
Реактивную мощность можно выразить также в виде
QL = U2L/XL или QL = I2XL
При последовательном соединении катушек индуктивности эквивалентная индуктивность Lэк равна сумме индуктивностей; например, при трех катушках с индуктивностями L1, L2 и L3 (рис. 180, а)
Lэк = L1+ L2 + L3
В этом случае эквивалентное индуктивное сопротивление
XLэк = XL1+ XL2 + XL3
При параллельном соединении катушек индуктивности (рис. 180,б) для эквивалентной индуктивности имеем:
1 /Lэк = 1 /L1 + 1 /L2 + 1 /L3
для эквивалентного индуктивного сопротивления
1 /XLэк = 1 /XL1 + 1 /XL2 + 1 /XL3
3)
Так как четырехполюсник характеризуется тремя независимыми коэффициентами, то из этого следует, что его простейшая схема замещения должна содержать три независимые элементы
Для этой схемы справедливы следующие соотношения:
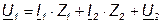
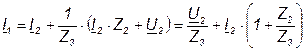
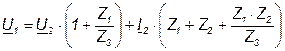 ; (7.9)
; (7.9)
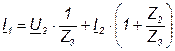 , (7.10)
, (7.10)
Сравнивая полученные уравнения 7.9 и 7.10 с системой уравнений формы А 7.1 и 7.2 записываем значения искомых величин:
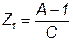
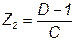
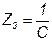
Билет 1
1)
Сформулируем 1-й закон Кирхгофа: сумма токов, сходящихся в узле эл. цепи, равна нулю.
При этом токи, стрелка которых направлена к узлу, входят в сумму с дополнительным знаком минус:
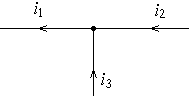 Рис. 2.1. Рис. 2.1. |
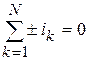 .
.
Например, для узла на рис. 2.1 имеем:
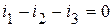 .
.
3)
Если каждому числу (точке) 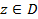 по некоторому правилу поставлено в соответствие определенное число (точка)
по некоторому правилу поставлено в соответствие определенное число (точка) 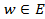 , то говорят, что на множестве определена однозначная функция комплексного переменного
, то говорят, что на множестве определена однозначная функция комплексного переменного 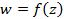 , отображающая множество D в множество Е.
, отображающая множество D в множество Е.
Если каждому 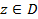 соответствует несколько значений w, то функция
соответствует несколько значений w, то функция 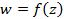 называется многозначной.
называется многозначной.
Множество D называется областью определения функции 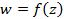 .
.
сновные элементарные функции комплексного переменного 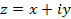 :
:
· показательную;
· логарифмическую;
· степенную;
· тригонометрическую;
Показательная функция 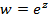 определяется формулой:
определяется формулой:
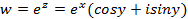 .
.
Логарифмическая функция определяется как функция, обратная показательной. Число w называют логарифмом числа 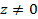 , если
, если 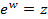 . Логарифмическая функция обозначается:
. Логарифмическая функция обозначается: 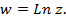 Так как значения показательной функции
Так как значения показательной функции 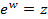 всегда отличны от нуля, то логарифмическая функция
всегда отличны от нуля, то логарифмическая функция 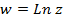 определена на всей плоскости z, кроме точки
определена на всей плоскости z, кроме точки 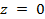 .
.
ригонометрические функции комплексного аргумента 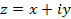 определяются равенствами:
определяются равенствами:
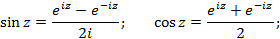
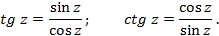
Дополнительно
П – образная схема (схема треугольника)
Аналогичные приёмы для П- схемы дают:
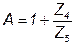 ;
;
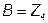 ;
;
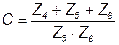 ;
;
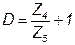 .
.
Тогда можно записать искомые значения сопротивлений:
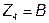 ;
;
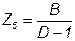 ;
;
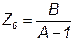 .
.
Второй закон Кирхгофа (Закон напряжений Кирхгофа, ЗНК) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:
для постоянных напряжений
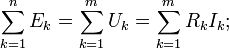
для переменных напряжений
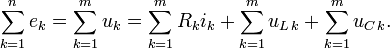
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит 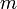 ветвей, из которых содержат источники тока ветви в количестве
ветвей, из которых содержат источники тока ветви в количестве 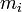 , то она описывается
, то она описывается 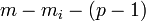 уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи.
