Методика выполнения контрольной работы

Если .

7. При дифференцировании произведения или частного нескольких функций, а также сложно-степенной функции целесообразно использоватьлогарифмическую производную:

если 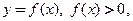то .

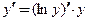Этот прием называют предварительным логарифмированием.

8. Правило дифференцирования параметрически заданной функции:

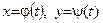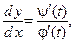если ,тоили.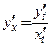

Задача на составление уравнений касательной и нормали

Касательную и нормаль, проходящие через точку 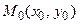, принадлежащую кривой, определяют три параметра: .

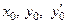à Если кривая задана явно уравнением 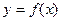, то 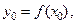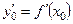. Если значение 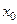не указано, то 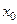надо найти из условий задачи.

à Если кривая задана параметрическими уравнениями: 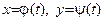, то y₀=y(t₀), x₀=j(t₀),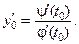

Если значение параметра 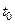не указано, то его надо определить, исходя из условий задачи, так как 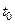используется при вычислении 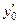и, возможно, какой-либо координаты точки .

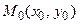Параметры 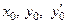удобно свести в таблицу:

Таблица 1

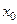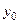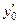Вид уравнений касательной и нормали определяется значением параметра 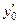. Различают три случая.

1. Если 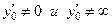, то

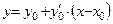− уравнение касательной,

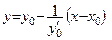− уравнение нормали.

2. Если 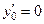, то

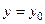− уравнение касательной,

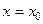− уравнение нормали.

3. Если 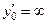, то

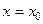− уравнение касательной,

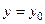− уравнение нормали.

В первом случае и касательная, и нормаль − наклонные прямые; во втором случае касательная − горизонтальная прямая (горизонталь), нормаль − вертикальная прямая (вертикаль); в третьем случае касательная − вертикальная прямая, нормаль − горизонтальная прямая.

ЗАДАЧА НА ПРИМЕНЕНИЕ ПРАВИЛА ЛОПИТАЛЯ

При вычислении пределов функций, связанных с раскрытием неопределенностей вида 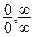, можно использовать правила Лопиталя-Бернулли: 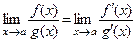, если существует предел 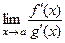. Здесь 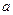− конечная или бесконечная величина.

Ниже приведены:

− методика выполнения контрольной работы;

− типовой вариант;

− пошаговое решение типового варианта.

Методика выполнения контрольной работы

При выполнении задач 1−3 следует:

1) определить способ задания функции − явный или параметрический;

2) в случае явного задания упростить функцию и выбрать подходящие правила дифференцирования, определить и реализовать последовательность их применения;

3) в случае параметрического задания функции воспользоваться правилом 7 параметрического дифференцирования и правилами 1-6 при нахождении производных .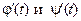

В задаче 4 следует:

1) определить способ задания функции − явный или параметрический;

2) в зависимости от способа задания функции выбрать формулы для вычисления параметров 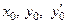искомых прямых, в частности:

○ для явной функции 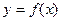параметр ;

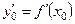○ для функции, заданной параметрическими уравнениями 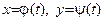, найти параметр по формуле ;

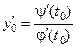3) заполнить табл. 1;

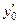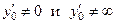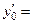4) по значению выбрать подходящий частный случай − один из трех: 1) , 2) 0; 3) 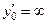) и составить уравнение касательной и/или уравнение нормали.

В задаче 5 следует использовать следующую методику.

1) Подставить предельное значение аргумента и найти предел или установить наличие неопределенности или отсутствие предела. В случае неопределенности определить ее вид.

2) Если неопределенность имеет вид 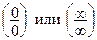, то составить новое предельное выражение 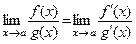согласно правилу Лопиталя. При отыскании производных числителя и знаменателя использовать методику дифференцирования явных функций.

Если получена неопределенность иного вида, то функцию надо преобразовать так, чтобы получилась неопределенность вида 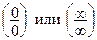и далее вернуться к началу этого пункта.

3)повторить пункты 1) и 2) данной методики для нового предельного выражения 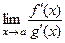. Заметим, что при неоднократном применении правила Лопиталя порядки производных будут расти.

Если в ходе применения правила Лопиталя получается выражение, не имеющее никакого предела, то следует использовать иной способ решения задачи − тождественные преобразования, эквивалентные функции, замечательные пределы или сочетание приемов.

Типовой вариант КР1

Найдите производные 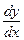функций:

1)

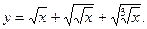
2)

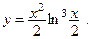
3)

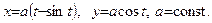
4) Напишите уравнение касательной к кривой 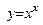в точке, где .

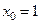5) Найдите предел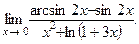

Или

Найдите предел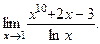

Или

Найдите предел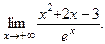

Задача 1. Найдите производную 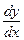функции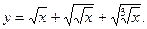

1-й шаг. Определяем способ задания функции. Функция задана явно. (Выбор одного ответа из двух возможных: явно или параметрически задана).

2-й шаг. Упрощаем функцию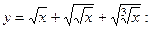

.

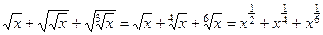Выбираем правило 1 для дифференцирования суммы: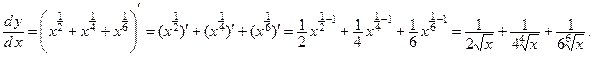

Задача 2. Найдите производную 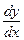функции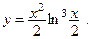

1-й шаг. Определяем способ задания функции. Функция задана явно. (Выбор одного ответа из двух возможных: явно или параметрически задана).

2-й шаг. Упростить функцию нельзя. Данная функция является произведением константы 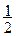и двух функций: 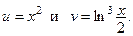Функция 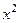− табличная, −

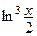нетабличная сложная функция: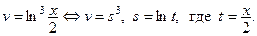

Выполним дифференцирование в следующем порядке:

− сначала выносим константу за знак производной по правилу 4:

;

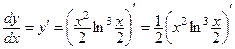− применяем правило 3 дифференцирования произведения:

;

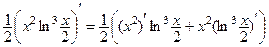− находим производные двух оставшихся функций:

по таблице производных ;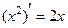

по правилу дифференцирования сложной функции:

;

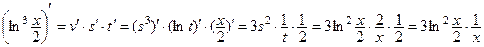− «собираем» ответ:

.

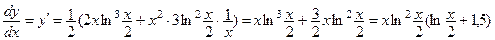Задача 3. Найдите производную 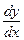функции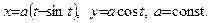

1-й шаг. Определяем способ задания функции. Функция задана параметрически. (Выбор одного ответа из двух возможных: явно или параметрически задана).

2-й шаг. Возможность упрощения функции отсутствует. Применяем правило 8 дифференцирования параметрически заданной функции:

.

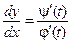В данном примере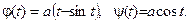

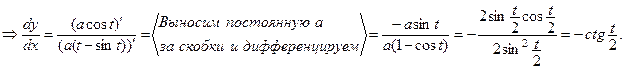
Задача 4. Напишите уравнение касательной к кривой 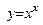в точке, где .

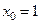1-й шаг. Определяем способ задания функции. Функция 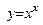задана явно. (Выбор одного ответа из двух возможных: явно или параметрически задана).

2-й шаг. Находим параметры касательной: 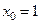из условий задачи, 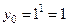, так как 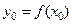. Вычисляем параметр 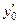по формуле 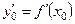. Функция 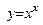является

сложно-степенной функцией, производную которой можно найти при помощи предварительного логарифмирования: 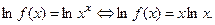Дифференцируем

обе части равенства по переменно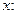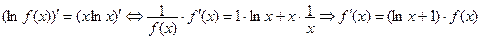й или

.

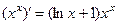При .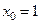

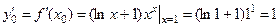3-й шаг. Заполним табл. 1:

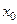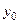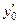4-й шаг. Так как 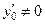и 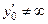, то имеем дело с 1-м случаем: 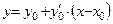− уравнение касательной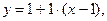, или или .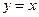

Задача 5. Найдите предел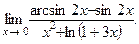

1-й шаг. Подставляем предельное значение аргумента в заданную функцию: 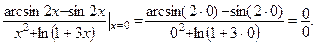Получена неопределенность, для раскрытия которой применимо правило Лопиталя.

2-й шаг. Согласно правилу Лопиталя составляем новое предельное выражение: 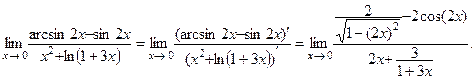Заметим, что при вычислении производных числителя и знаменателя использованы правила 1, 2, 6 и таблица производных.

3-й шаг. Подставляем предельное значение аргумента в новую функцию: =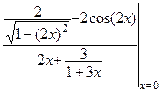

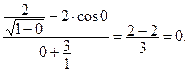
Или

Задача 5. Найдите предел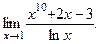

1-й шаг. Подставляем предельное значение аргумента в заданную функцию: 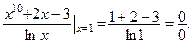Получаем неопределенность вида 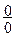, для раскрытия которой применяем правило Лопиталя.

2-й шаг. Согласно правилу Лопиталя составляем новое предельное выражение: 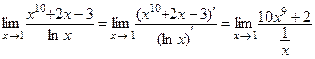. При вычислении производных числителя и знаменателя использованы правила 1, 2 и таблица производных.

3-й шаг. Подставляем предельное значение аргумента в новую функцию: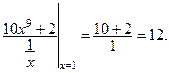

Или

Задача 5. Найдите предел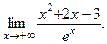

1-й шаг. Подставляем предельное значение аргумента в заданную функцию: 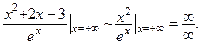Получаем неопределенность вида 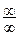, для раскрытия которой применяем правило Лопиталя.

2-й шаг. Согласно правилу Лопиталя составляем новое предельное выражение: 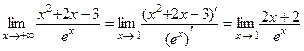. При вычислении производных числителя и знаменателя использованы правила 1, 2 и таблица производных.

3-й шаг. Подставляем предельное значение аргумента в новую функцию: 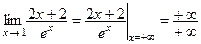. Получаем неопределенность вида 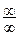, для раскрытия которой повторно применяем правило Лопиталя.

4-й шаг. Составляем новое предельное выражение: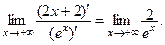

5-й шаг. Вычисляем предел и получаем ответ: 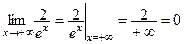.