Метод допустимых направлений

Данный метод также называется методом возможных направлений или по имени автора - методом Зойтендейка. Его основную идею удобно продемонстрировать на примере ЗИП с ограничениями в форме неравенств:

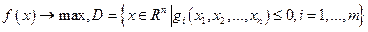. (16)

В указанном методе так же, как и в градиентных методах, находится последовательность точек 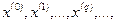таких, что 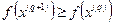. При этом переход от точки 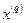кточке происходит по некоторому выбранному направлению 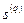с шаговым множителем :

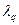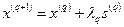. (17)

По отношению к векторам, задающим направления перемещения, вводятся два фундаментальных понятия.

1. Направление s называется допустимым(возможным) в точке 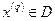, если существует такое 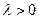, что .

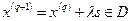2. Направление s называется прогрессивнымв точке 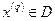, если существует такое 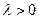, что 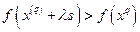для задачи максимизации и 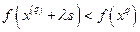для задачи минимизации.

На основе данных определений сформулируем критерий проверки оптимальности точки (так называемый критерий оптимальности в терминах допустимых и прогрессивных направлений).

Точка 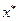является оптимальным планом задачи (16), если в ней ни одно допустимое направление не является прогрессивным.

В алгоритме метода допустимых направлений правила выбора точки 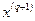к которой происходит очередной переход, различаются в зависимости от того, где находится текущая точка 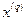. Принципиально возможны две ситуации.

1°. Точка 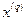лежит внутри области D, т. е. для всех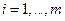 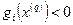(Рис. 2.4). Очевидно, что для внутренней точки любое направление является допустимым (при выборе достаточно малого шага), поэтому естественным представляется движение в сторону «гарантированного» возрастания значения функции, а именно в направлении градиента. Следовательно, для внутренней точки 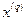целесообразно выбрать .

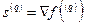Шаговый множитель 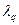выбирается так, чтобы, с одной стороны, новая точка 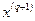принадлежала D, а с другой - значение целевой функции в ней 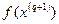было как можно большим.

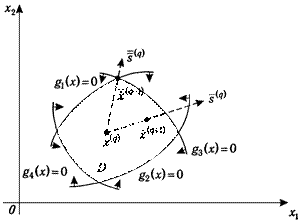
Рис. 2.4

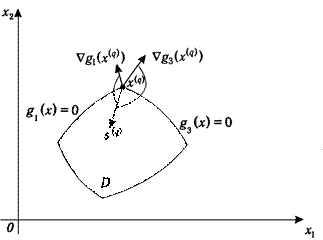
Рис. 2.5

Для этого сначала находим промежуток 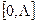из условия 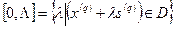, для чего необходимо решить систему неравенств:

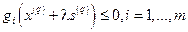. (18)

Зная промежуток 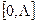, определяем значение шагового множителя 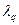из условия максимизации значения функции в направлении :

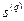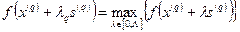. (19)

Вновь найденная точка 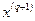может находиться или внутри области D, или на ее границе. В первом случае (на Рис. 2.4ему соответствует точка 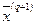) переходим к началу данного пункта и повторяем вышеописанные действия, а во втором (точка 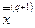на Рис. 2.4) - действуем по рассматриваемой далее схеме.

2°. Точка 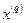находится на границе области(Рис. 2.5).Это означает, что одно или несколько неравенств из системы ограничений задачи (16) выполняются как строгие равенства: 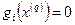. Например, на Рис. 2.5 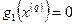и .

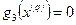Ограничение, которое в текущей точке выполняется как равенство, называют активным. Множество номеров активных ограничений в точке 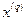будем обозначать как 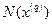. В примере, изображенном на Рис. 2.5, 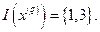Также из рисунка видно, что все допустимые направления, исходящие из точки 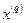должны образовывать тупые углы с векторами градиентов функций, задающих активные ограничения в данной точке. Последнее условие может быть выражено через задание ограничений на значения скалярных произведений вектора направления s на градиенты функции ограничений:

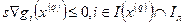, (20)

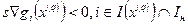, (21)

где I_л - множество номеров индексов линейных ограничений, I_н - множество номеров индексов нелинейных ограничений. Соответственно, 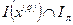- номера линейных активных ограничений, a 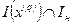- номера нелинейных активных ограничений. Отличие условий (20) от условий (21) заключается в том, что в случае линейного ограничения направление, образующее прямой угол с градиентом ограничивающей функции (т. е. их скалярное произведение равно нулю), будет заведомо допустимым, а в случае нелинейного ограничения - возможно, нет.

Все возможные направления в точке 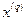образуют так называемый конус допустимых направлений, и из них для следующего перехода, очевидно, нужно выбрать прогрессивное. Если такого не существует, то согласно сформулированному выше критерию точка 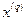является оптимальной. Для ускорения максимизации функции желательно, чтобы угол между искомым допустимым прогрессивным направлением 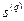и градиентом целевой функции 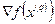был как можно меньше или, что то же самое, как можно большей была бы проекция s на 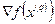(при условиях нормировки вектора 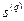). Другими словами, желательно, чтобы неравенство 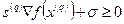выполнялось при минимально возможном 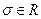.Тогда задачу отыскания наилучшего допустимого прогрессивного направления 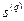можно свести к задаче минимизации параметра :

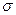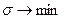(22)

при условиях

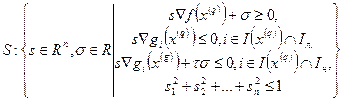(23)

где 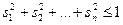- условие нормировки, обеспечивающее ограниченность решения; 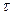- некоторое достаточно малое число, характеризующее «строгость» выполнения неравенств.

В отличие от всех остальных, последнее условие в системе (23) является нелинейным, что существенно усложняет процесс решения задачи (22)-(23). Поэтому на практике для определения направления 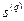(возможно, не лучшего) переходят от данной задачи к задаче линейного программирования путем замены указанных выше условий нормировки на ограничения вида :

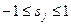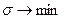(24)

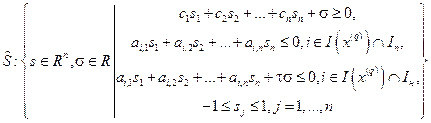(25)

где , .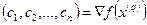

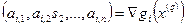После того как прогрессивное направление 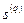найдено, шаговый множитель определяется по методу, описанному в п. 1°.

В заключение заметим, что

1. при практических расчетах алгоритм завершается при достижении такой точки 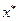, в которой 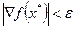, где e - достаточно малое число.

2.применяемый для решения задач линейного программирования симплекс-метод может быть рассмотрен как частный случай метода допустимых направлений. В частности, этап выбора столбца, вводимого в очередной базис, соответствует определению допустимого прогрессивного направления.

Пример решения ЗНП методом допустимых направлений.Рассмотрим процесс применения метода допустимых направлений на конкретном примере. Пусть дана ЗНП:

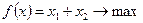(26)

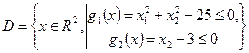. (27)

Итерация 1.В качестве начального приближения выберем точку 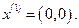Нетрудно заметить, что она удовлетворяет системе неравенств (27), т. е. 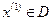. Для 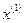все неравенства выполняются как строгие, т. е. множество индексов активных ограничений 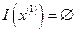. Следовательно, в 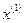любое направление является допустимым, и остается определить, с каким шагом 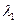, можно двигаться вдоль градиента целевой функции 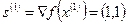. Система неравенств типа (18), из решения которых определяется интервал допустимых значений для 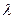, для данной задачи имеет вид:

.

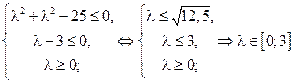Тогда

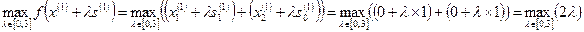
достигается при 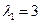. Отсюда получаем следующую точку

.

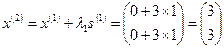Итерация 2.Путем подстановки координат точки 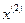в (27) определим множество активных ограничений в точке 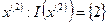. Соответственно, задача (24) - (25), которую требуется решить для определения допустимого прогрессивного направления 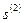с учетом того, что 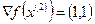и 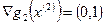, примет вид:

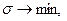
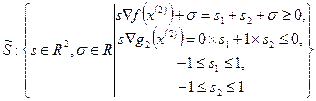
В данном случае оптимальный план ЗЛП находится довольно просто и равен 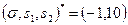. Отбросив дополнительную переменную 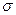, получаем вектор 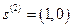, т. е. очередная точка будет определяться как

.

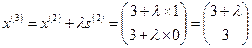Действуя по аналогии с предыдущей итерацией, для определения промежутка допустимых значений шагового множителя 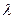составляем систему неравенств (18):

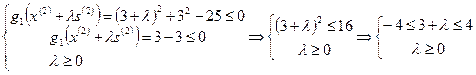
Окончательно имеем 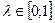. Тогда

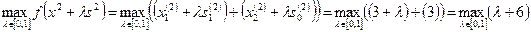
достигается при 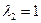. Отсюда получаем следующую точку .

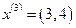Итерация 3.В точке 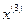множество активных ограничений имеет вид 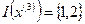. Найдем значения градиентов: 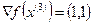, 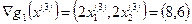и .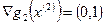

Задача определения допустимого прогрессивного направления (24)-(25) примет вид:

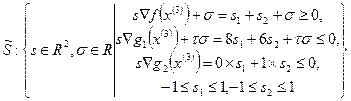
Значение 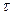из практических соображений следует брать достаточно малым, например 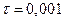. Опуская решение данной задачи, приведем искомые компоненты ее оптимального плана: 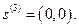Итак, не существует прогрессивного направления, исходящего из точки 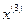. Таким образом, оптимальный план рассматриваемой задачи (26)-(27) 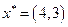, а максимальное значение целевой функции .

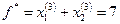Графическая иллюстрация проведенного процесса решения представлена графически на Рис. 2.6.

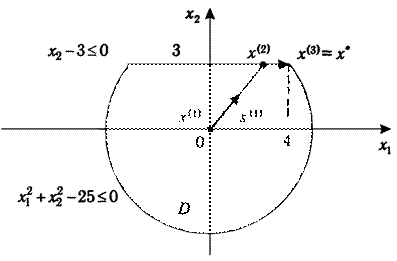
Рис. 2.6