Системы линейеых уравнений
Вычисление определителей
Определение 1.2..Каждой квадратной матрице A = 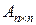 можно сопоставить число detA либо |A| или D, которое называют определителем матрицы и находят
можно сопоставить число detA либо |A| или D, которое называют определителем матрицы и находят
следующим образом:
1. Если 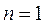 , т.е.
, т.е. 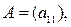
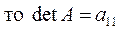 ;
;
2. Если 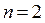 , т.е.
, т.е.
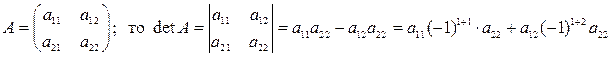 ;
;
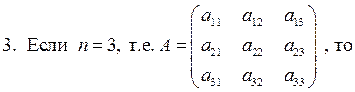
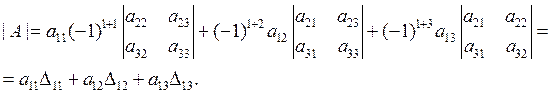
4. В общем случае, если A = 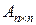 , то detA находится с помощью разложения Лапласа:
, то detA находится с помощью разложения Лапласа: 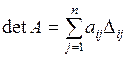 , где
, где 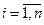 , а
, а 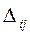 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 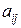 , матрицы A =
, матрицы A = 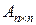 , т.е.
, т.е.
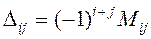 ,
,
и  - минор элемента
- минор элемента 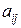 , т.е. определитель квадратной матрицы А =
, т.е. определитель квадратной матрицы А = 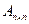 , полученный из неё путём вычеркивания i-ой строки и j-ого столбца, на пересечении которых стоит элемент
, полученный из неё путём вычеркивания i-ой строки и j-ого столбца, на пересечении которых стоит элемент 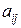
Пример.1.2 Дана квадратная матрица 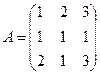
Найти её определитель detA.
Решение. Найдём detA, применив разложение Лапласа по элементам первой строки матрицы A:
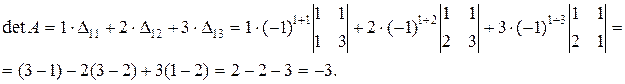
Пример 1.3
Вычислим определитель
Для этого в начале преобразуем его с помощью элементарных преобразований:
∆ = 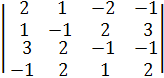 =( С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=( С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 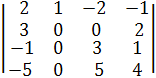 ,чтобы получить побольше нулей. Раскроем затем этот определитель по элементам второго столбца по правилу Лапласа. Получим
,чтобы получить побольше нулей. Раскроем затем этот определитель по элементам второго столбца по правилу Лапласа. Получим
∆ =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 = а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙
(-1)3+2М 32 + а42∙(-1)4+2М 42=1∙(-1)2+1 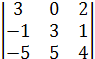 +0+0+0 = (-1)
+0+0+0 = (-1) 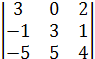 .
.
Раскроем полученный определитель по первой строке:
∆ = - 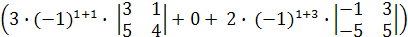 = - (3∙(3∙4 -1∙5)+0 + +2∙ (-1∙5- 3∙(-5)) = -( 3∙7+2∙10)=-41.
= - (3∙(3∙4 -1∙5)+0 + +2∙ (-1∙5- 3∙(-5)) = -( 3∙7+2∙10)=-41.
Операции над матрицами
Вычислить А2 - 3АВ, где
А = 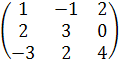 В =
В = 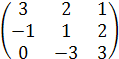
Решение. Находим матрицу
А2 =А∙А = 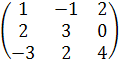 ∙
∙ 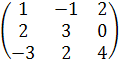 .
.
Для получения элемента , стоящего в первой строке и в первом столбце, перемножим соответствующие элементы первой строки матрицы А и элементы первого столбца матрицы В (т.е первый элемент первой строки матрицы А умножим на первый элемент первого столбца матрицы В; второй элемент первой строки матрицы А на второй элемент первого столбца матрицы В; третий элемент первой строки матрицы А умножим на третий элемент первого столбца матрицы В)и их произведения сложим.Для получения элемента , стоящего в первой строке и во втором столбце, перемножим соответствующие элементы первой строки матрицы А и элементы второго столбца матрицы В и их произведения сложим и т.д. В итоге получим матрицу размером 3×3:
А2 = 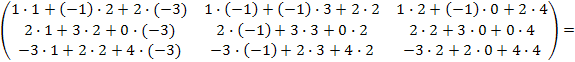
= 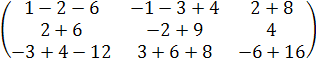 =
= 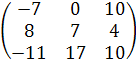
Аналогично находим матрицу 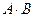 :
:
А∙В = 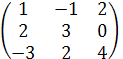 ∙
∙ 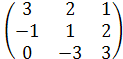 =
=
= 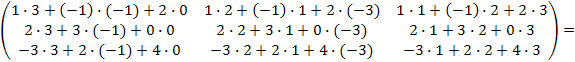
= 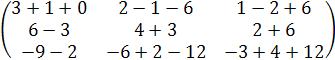 =
= 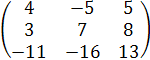
Вычисляем затем матрицу
3∙А∙В = 3∙ 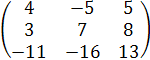 = (Чтобы умножить матрицу на число, надо каждый элемент этой матрицы умножить на это число.)=
= (Чтобы умножить матрицу на число, надо каждый элемент этой матрицы умножить на это число.)= 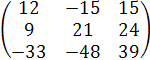 .
.
Таким образом, получим , что матрица
А2 - 3АВ = 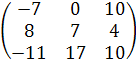 -
- 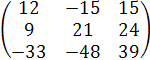 = (Чтобы сложить две матрицы, надо сложить их соответствующие элементы.)=
= (Чтобы сложить две матрицы, надо сложить их соответствующие элементы.)= 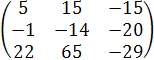 .
.
Системы линейеых уравнений
ПримерРешить методом Гаусса СЛАУ вида
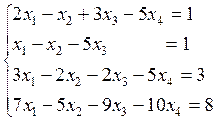
Здесь число неизвестных n= 4.
Решение. Приведём расширенную матрицу 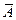 этой СЛАУ путём элементарных преобразований нал её строками к ступенчатому виду
этой СЛАУ путём элементарных преобразований нал её строками к ступенчатому виду

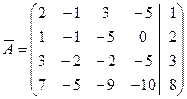 ~
~ 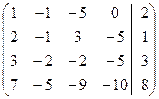 ~
~
~ 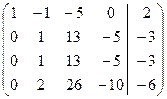 ~
~ 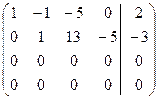
На основании этого СЛАУ запишется в эквивалентном ступенчатом виде:
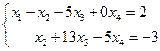
Так как для матрицы A данной системы её ранг 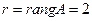 < 4, то эта система имеет бесконечное множество решений, из которых 2 являются базисными. Положим
< 4, то эта система имеет бесконечное множество решений, из которых 2 являются базисными. Положим 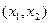 за базисное решение, так как в матрице A системы имеется соответствующий им базисный минор
за базисное решение, так как в матрице A системы имеется соответствующий им базисный минор 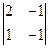 ¹.0. Тогда полученную систему запишем в эквивалентном виде:
¹.0. Тогда полученную систему запишем в эквивалентном виде:
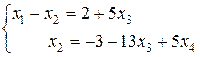 .
.
Из этой системы обратным ходом находим базисные неизвестные
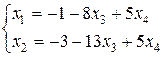 .
.
Здесь 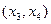 - свободные неизвестные или параметры. Если положить
- свободные неизвестные или параметры. Если положить 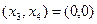 , то получим соответствующее частное решение системы
, то получим соответствующее частное решение системы
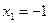 ;
; 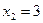 ;
; 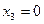 ;
; 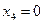 .
.
Пример
.Решить методом Гаусса СЛАУ
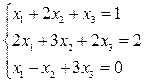
Решение. Приведём расширенную матрицу 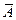 этой СЛАУ с помощью элементарных преобразований над её строками к ступенчатому виду:
этой СЛАУ с помощью элементарных преобразований над её строками к ступенчатому виду:
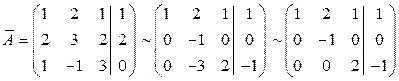 .
.
На основании этого СЛАУ запишется в эквивалентном треугольном виде:
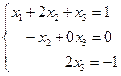
Отсюда методом обратного хода получаем её единственное решение:
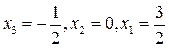 .
.
Пример 1.4. Решить однородную систему уравнений:
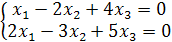
Решение. Здесь 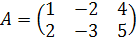 , и r(A) = 2, т.к. в матрице А имеется минор
, и r(A) = 2, т.к. в матрице А имеется минор 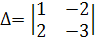 =1¹0; а п =3. Следовательно r(A) < п , т.е. эта система имеет бесконечное множество решений. Так как существует базисный минор
=1¹0; а п =3. Следовательно r(A) < п , т.е. эта система имеет бесконечное множество решений. Так как существует базисный минор 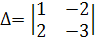 =1¹0 матрицы А, то можно записать данную систему следующим образом:
=1¹0 матрицы А, то можно записать данную систему следующим образом:
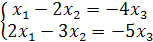 .
.
Найдём её решение по методу Крамера (6.3). Имеем
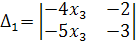 = 2x3;
= 2x3; 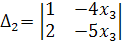 = 3x3.
= 3x3.
Отсюда, по формулам (6.3) получим 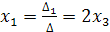 ;
; 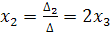 . Здесь x1,x2 – базисные неизвестные, а x3 – параметр. Если положить, что параметр х3=0, то х1=0, х2=0; т.е. получим частное решение системы, а если х3=1, то х1=2, х2=3, то находим второе частное решение.
. Здесь x1,x2 – базисные неизвестные, а x3 – параметр. Если положить, что параметр х3=0, то х1=0, х2=0; т.е. получим частное решение системы, а если х3=1, то х1=2, х2=3, то находим второе частное решение.
Пример
Найти решение и ФСР однородной СЛАУ.
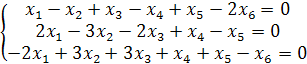
Решение. Решим эту систему методом Гаусса. Так как для ОСЛАУ расширенная матрица 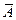 совпадает с её матрицей A ,то рассмотрим матрицу
совпадает с её матрицей A ,то рассмотрим матрицу
А = 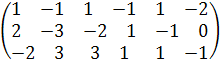
и введём элементарные преобразование над строками этой матрицы в виде схематичных равенств С2:= 2С1+ С2; С3:= 2С1+ С3 , где 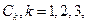 -обозначения строк матрицы A. В результате получим, что
-обозначения строк матрицы A. В результате получим, что
A ~ 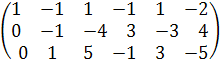 (С3:= С2+ С3 ) ~
(С3:= С2+ С3 ) ~ 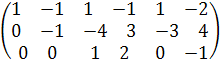
Отсюда видно, что r(A) =3, т.е. ФСР состоит из п - r = 6 -3=3 решений. Чтобы найти ее, выберем х1, х2, х3 за базисные переменные. Тогда система запишется в эквивалентной форме вида
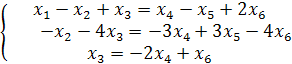
Обратный ход метода Гаусса дает значение базисных неизвестных х1, х2, х3 через значения свободных переменных х4, х5, х6:
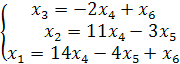 или
или 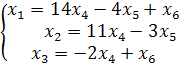
Присваивая для х4 значения (1,0,0), для х5 значения (0,1,0), для х6 значения (0,0, 1) находим последовательно из полученной системы соответствующие частные значения для базисных переменных х1, х2, х3 в виде таблицы:
| х1 | х2 | х3 |
| -2 | ||
| -4 | -3 | |
Таким образом, ФСР для данной СЛАУ имеет вид:
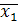 =(14, 11,-2,1,0,0)
=(14, 11,-2,1,0,0)
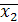 =(-4, -3, 0,0,1,0)
=(-4, -3, 0,0,1,0)
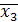 =(1, 0,1,0,0,1)
=(1, 0,1,0,0,1)
Решить систему уравнений
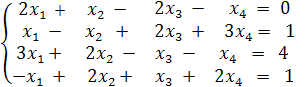 (1)
(1)
1) методом Гаусса;
2) по правилу Крамера;
3) матричным способом.
Решение.
1).Метод Гаусса. Составим расширенную матрицу, соответствующую данной системе (1):
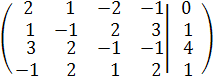
Приведем эту матрицу к треугольному виду с помощью элементарных преобразованийнад её строками, а именно:
- перестановкой строк;
- умножением элементов строки матрицы на число;
- сложением соответствующих (стоящих на одинаковых местах) элементов двух строк и помещение сумм этих элементов на место соответствующих элементов одной из складываемых строк.
Чтобы привести матрицу к треугольному виду надо получить нули на месте элементов, стоящих под главной диагональю. Сперва получим нули в первом столбце , находящиеся, во второй, третьей и четвертой строках, т.е. надо изменить вторую, третью, четвертую строки. Так как первая строка не изменяется, изменения в других строках будем производить относительно нее: выберем на главной диагонали неизменяемой строки главный элемент, в нашем примере это 2. Если в столбце, в котором мы хотим получить нули, имеется 1, то для облегчения счета строку с1 на первом месте лучше поставить на место первой строки и сделать ее, тем самым, неизменяемой.
Внашем примере , вторая строка содержит на первом месте 1. Поменяем ее с первой строкой. Эту операцию обозначим следующим образом:

 С2 С1,
С2 С1,
(здесь С2 –обозначение второй строки, С1 – первая строка). При этом получим эквивалентную матрицу
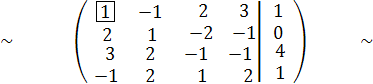
Теперь главным элементом будет 1.Обведем ее в квадрат. Чтобы получить на месте 2 во второй строке 0, надо каждый элмент первой строки умножить на (-2) и сложить с соответствующим элементом второй строки и их сумму записать на место соответствующего элемента второй строки. Эту операцию обозначим следующим образом:
С2 := -2∙С1 + С2,
(здесь := - это оператор присваивания, т.е. значение выражения с правой стороны записывается на место величины, стоящей слева). При этом получим эквивалентную матрицу
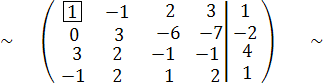
Чтобы получить вместо числа 3 нуль в третьей строке, проделаем операцию С3 := -3∙С1 + С3, а чтобы получить вместо (-1) нуль в четвёртой , проделаем операциюС4 := С1 + С4.В результате получим эквивалентную матрицу
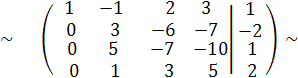
Теперь нужно получить нули во втором столбце в строках три и четыре, т.е. изменяемыми будут третья и четвертая строки. Выберем главный элемент в неизменяемой второй строке во втором столбце и который стоит на главной диагонали ( в примере это 3), но среди изменяемых строк имеется четвёртая строка, в которой во втором столбце стоит 1.Поэтому поменяем ее со второй строкой , в которой мы выбрали главный элемент (т.е. надо поменять местами вторую и четвертую строчки):

 С4 С2 .При этом получим эквивалентную матрицу
С4 С2 .При этом получим эквивалентную матрицу
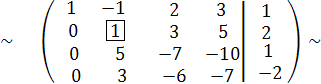
Теперь главным элементом будет элемент 1. Заключим его в квадат.Что-бы получить вместо 5 нуль в третьей строке, проделаем операциюС3 := -5∙С2 + С3, а чтобы получить вместо 3 нуль в четвёртой строке, проделаем операцию С4 := -3С2 + С4. В итоге получим эквивалентную матрицу
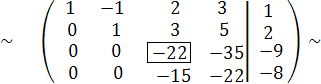
Осталось получить нуль в третьем столбце четвертой строки. Главный элемент выбираем в третьем столбце и третьей строке (это -22).Так как изменяемой будет только четвертая строка и среди изменяемых строк в третьем столбце нет единицы, то (-22) и будет главным элементом. Чтобы получить вместо -15 нуль в четвёртой строке, проделаем следующую операцию
С4 :=- 15∙С3 +22∙ С4.При этом получим эквивалентную матрицу
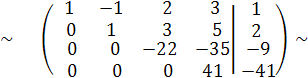
Разделим последнюю строчку полученной матрицы на 41,т.е. проведём операцию С4 := С4 : 41. Получим эквивалентную матрицу
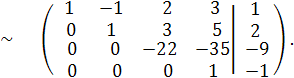
Построим по полученной матрице эквивалентную (1) систему уравнений.
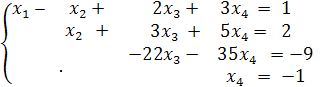
Из последнего уравнения находим x4 = -1. Применяя метод обратного хода, подставим это значение в предпоследнее уравнение. Получим:
- 22x3 - 35∙ (-1) = -9. Отсюда получим,что
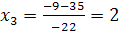 .
.
Подставляя найденные значения х4 и х3 во второе уравнение , получим
x2 +3∙2 + 5∙(-1) = 2 , откуда x2 = 2 – 6 +5 =1. Подставляя затем найденные значения для x4 , х3 и x2 в первое уравнение получим
x1 - 1 + 2∙2 +3∙(-1) = 1 или x1 = 1.
Ответ: 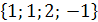 .
.
2).Решим эту систему по правилу Крамера,применяя формулы(6.3). 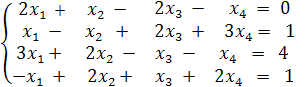 .
.
Составим матрицу, соответствующую данной системе:
А = 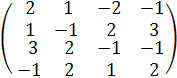 ,
,
и запишем столбец свободных членов системы:
В = 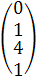 .
.
Вычислим главный определитель системы, отвечающий матрице А. Для этого в начале преобразуем его с помощью элементарных преобразований:
∆ = 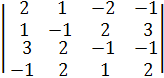 =( С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=( С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 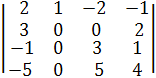 ,чтобы получить побольше нулей. Раскроем затем этот определитель по элементам второго столбца по правилу Лапласа. Получим
,чтобы получить побольше нулей. Раскроем затем этот определитель по элементам второго столбца по правилу Лапласа. Получим
∆ =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 = а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙
(-1)3+2М 32 + а42∙(-1)4+2М 42=1∙(-1)2+1 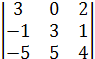 +0+0+0 = (-1)
+0+0+0 = (-1) 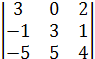 .
.
Раскроем полученный определитель по первой строке:
∆ = - 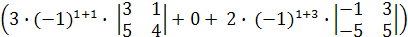 = - (3∙(3∙4 -1∙5)+0 + +2∙ (-1∙5- 3∙(-5)) = -( 3∙7+2∙10)=-41.
= - (3∙(3∙4 -1∙5)+0 + +2∙ (-1∙5- 3∙(-5)) = -( 3∙7+2∙10)=-41.
Чтобы получить определитель ∆х, заменим первый столбец в главном определителе ∆ на столбец свободных членов.
∆х = 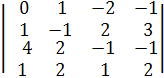 =(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 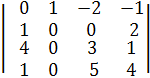 .
.
Раскроем этот определитель по элементам второго столбца:
∆х =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 == а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙
(-1)3+2М 32 + а42∙(-1)4+2М 42=1∙(-1)2+1 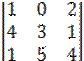 +0+0+0 = (-1)
+0+0+0 = (-1) 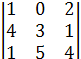 .
.
Раскроем полученный определитель по первой строке:
∆х = - 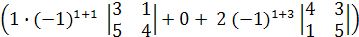 = - (1∙(3∙4 -1∙5)+0 +
= - (1∙(3∙4 -1∙5)+0 +
+2∙ (4∙5- 3∙1) = - ( 1∙7+2∙17)= - 41.
Чтобы получить определитель ∆у, заменим второй столбец в главном определителе ∆ на столбец свободных членов.
∆у = 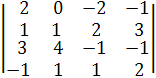 =(С3 := -4∙С2 + С3, С4 := -С2 + С4 )=
=(С3 := -4∙С2 + С3, С4 := -С2 + С4 )=
= 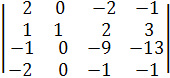 =
=
Вынесем минус за знак определителя из третей и четвертой строк, получим
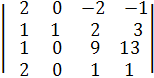
Раскроем этот определитель по элементам второго столбца:∆у =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 == а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙
(-1)3+2М 32 + а42∙(-1)4+2М 42==0 + 1∙(-1)2+2 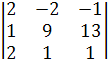 +0+0 =
+0+0 = 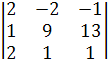 .
.
Раскроем полученный определитель по правилу треугольника:
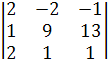 =2∙9∙1 + 2∙(-2)∙13 + (-1)∙1∙1 –(-1)∙9∙2 - 1∙(-2)∙1 - 2∙1∙13 = 18-52-1 +18 +2 -26= =-41 =∆у..
=2∙9∙1 + 2∙(-2)∙13 + (-1)∙1∙1 –(-1)∙9∙2 - 1∙(-2)∙1 - 2∙1∙13 = 18-52-1 +18 +2 -26= =-41 =∆у..
Чтобы получить определитель ∆z, заменим третий столбец в главном определителе ∆ на столбец свободных членов:
∆z = 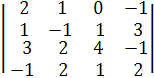 =(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 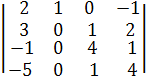 .
.
Раскроем этот определитель по элементам второго столбца:
∆z =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 = а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙
(-1)3+2М 32 + а42∙(-1)4+2М 42=1∙(-1)2+1 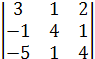 +0+0+0 = -
+0+0+0 = - 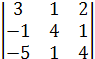 .
.
Раскроем полученный определитель по правилу треугольника:
∆z =- (3∙4∙4 +1∙1∙(-5) + 1∙(-1)∙2 - 2∙4∙(-5) - 1∙1∙3 - 1∙(-1)∙4) =
=-(48 -5 -2 +40 -3+4)=-82
Чтобы получить определитель ∆t, заменим четвертый столбец в главном определителе ∆ на столбец свободных членов.Получим
∆t = 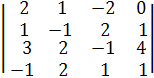 =(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 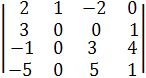 .
.
Раскроем этот определитель по элементам второго столбца:
∆t =а12∙А12 + а22∙А22 + а32∙А32 + а42∙А42 =
= а12∙(-1)1+2М12 + а22∙(-1)2+2М 22 + а32∙(-1)3+2М 32 + а42∙(-1)4+2М 42=
=1∙(-1)2+1 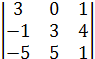 +0+0+0 = -
+0+0+0 = - 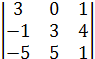 .
.
Раскроем полученный определитель по правилу треугольника:
∆t =- (3∙3∙1 +0∙4∙(-5) + 1∙(-1)∙5 - 1∙3∙(-5) - 0∙1∙(-1) - 5∙3∙4) =
=-(9 +0 -5 +15 +0-60) = 41.
Тогда
x = 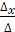 =
= 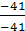 =1; y =
=1; y = 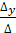 =
= 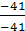 =1; z =
=1; z = 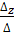 =
= 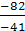 = 2; t =
= 2; t = 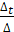 =
= 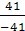 = - 1.
= - 1.
Ответ: 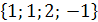 .
.
Обратная матрица
Запишем систему (1)
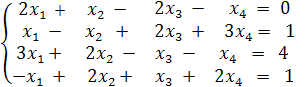 .
.
через произведение матриц по формуле (2.3). Для этого составим матрицу, соответствующую данной системе:
А = 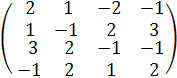 ,
,
столбец свободных членов В = 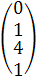 и столбец неизвестных Х =
и столбец неизвестных Х = 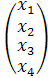 .
.
Тогда система уравнений запишется в матричном виде
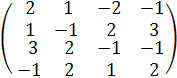 ∙
∙ 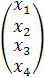 =
= 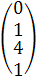 ,
,
т.е. А∙Х =В .Откуда находим,что Х = А-1∙В.
Найдем обратную матрицу А-1. Для этого
1) вычислим главный определитель матрицы
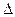 =
= 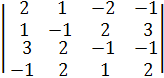 =(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
=(С2 := С1 + С2, С3 := -2∙С1 + С3, С4 := -2∙С1 + С4)=
= 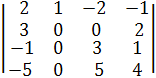 = 1∙(-1)2+1
= 1∙(-1)2+1 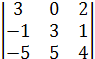 +0+0+0 =
+0+0+0 =
= - 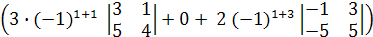 = - (3∙(3∙4 -1∙5)+0 +
= - (3∙(3∙4 -1∙5)+0 +
2∙ (-1∙5- 3∙(-5)) = - ( 3∙7+2∙10)= - 41.
2) построим матрицу ( 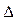 ij ) из алгебраических дополнений
ij ) из алгебраических дополнений 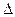 ij элементов матрицы А.
ij элементов матрицы А.
Найдем эти алгебраические дополнения (определители вычисляем по правилу треугольника):
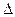 11 = (-1)1+1 ∙
11 = (-1)1+1 ∙ 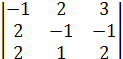 = 2 - 4 +6+6-1-8 = 1,
= 2 - 4 +6+6-1-8 = 1,
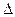 12 = (-1)1+2 ∙
12 = (-1)1+2 ∙ 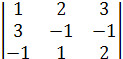 = -(-2 + 2 +9 - 3+1- 12) = 5,
= -(-2 + 2 +9 - 3+1- 12) = 5,
 13 = (-1)4 ∙
13 = (-1)4 ∙ 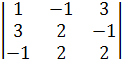 = 4 - 1 + 18+6 +2+6 = 35,
= 4 - 1 + 18+6 +2+6 = 35,
 14 = (-1)5 ∙
14 = (-1)5 ∙ 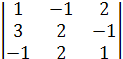 = -(2 - 1 + 12+ 4+2 + 3 ) = -22,
= -(2 - 1 + 12+ 4+2 + 3 ) = -22,
 21 = (-1)3 ∙
21 = (-1)3 ∙ 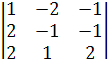 = -(-2 + 4 - 2- 2+1+ 8) = -7,
= -(-2 + 4 - 2- 2+1+ 8) = -7,
 22 = (-1)4 ∙
22 = (-1)4 ∙ 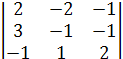 = -4 - 2 - 3+ 1+2+ 12 = 6,
= -4 - 2 - 3+ 1+2+ 12 = 6,
 23 = (-1)5 ∙
23 = (-1)5 ∙ 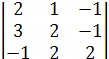 =-(8 - 6 + 1- 2 + 4- 6 ) = 1,
=-(8 - 6 + 1- 2 + 4- 6 ) = 1,
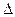 24 = (-1)6 ∙
24 = (-1)6 ∙ 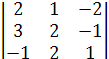 = 4 + 1 – 12 – 4 + 4- 3 = -10,
= 4 + 1 – 12 – 4 + 4- 3 = -10,
 31 = (-1)4 ∙
31 = (-1)4 ∙ 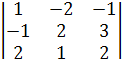 = 4 - 12 +1+4-4-3 = -10,
= 4 - 12 +1+4-4-3 = -10,
 32 = (-1)5 ∙
32 = (-1)5 ∙ 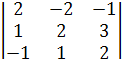 = -(8 - 1 +6 - 2- 6+ 4) = -9,
= -(8 - 1 +6 - 2- 6+ 4) = -9,
 33 = (-1)3+3 ∙
33 = (-1)3+3 ∙ 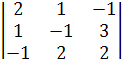 = -4 - 3 - 2+ 1- 12- 2 = -22,
= -4 - 3 - 2+ 1- 12- 2 = -22,
 34 = (-1)7 ∙
34 = (-1)7 ∙ 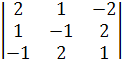 = -(-2 - 2 - 4+ 2-8- 1) = 15,
= -(-2 - 2 - 4+ 2-8- 1) = 15,
 41 = (-1)5 ∙
41 = (-1)5 ∙ 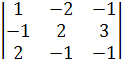 = -(-2 - 1 – 12 +4 + 3 + 2) = 6,
= -(-2 - 1 – 12 +4 + 3 + 2) = 6,
 42 = (-1)6 ∙
42 = (-1)6 ∙ 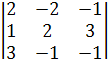 = -4 – 18 + 1+6 + 6- 2 = -11,
= -4 – 18 + 1+6 + 6- 2 = -11,
 43 = (-1)7 ∙
43 = (-1)7 ∙ 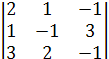 = -(2 - 2 + 9 - 3-12 +1 ) = 5 ,
= -(2 - 2 + 9 - 3-12 +1 ) = 5 ,
 44 = (-1)8 ∙
44 = (-1)8 ∙ 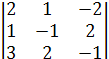 = 2- 4 +6 - 6- 8+ 1 = -9.
= 2- 4 +6 - 6- 8+ 1 = -9.
Полчили матрицу
(  ij ) =
ij ) = 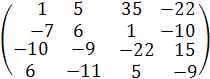 .
.
3) Находим присоединённую матрицу ( 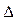 ji )= (
ji )= ( 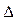 ij )T :
ij )T :
( 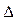 ji ) =
ji ) = 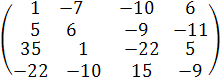 .
.
4) Получаем по формуле (2.2) обратную матрицу
А-1 = 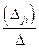 =
= 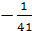 ∙
∙ 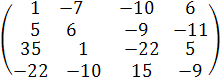 =
=
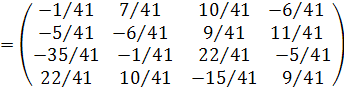
Тогда
Х = 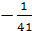 ∙
∙ 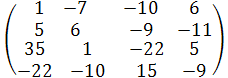 ∙
∙ 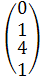 =
=
= 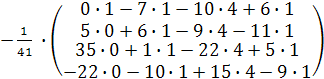 =
= 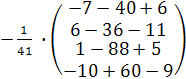 = =
= = 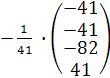 =
= 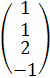 .
.
Ответ: 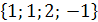 .
.
Рассмотрим второй способ получения обратной матрицы А-1 .
Используется формула вида (9.9):
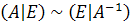 ,
,
где Е – единичная матрица; А – заданная матрица; 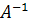 - обратная матрица.
- обратная матрица.
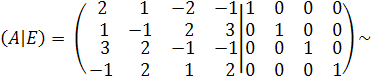

 С1 С2
С1 С2
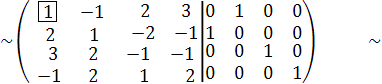
С2 := -2∙С1 + С2,
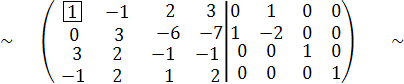
С3 := -3∙С1 + С3, С4 := С1 + С4,
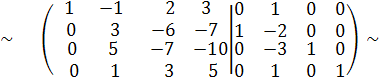

 С4 С2
С4 С2
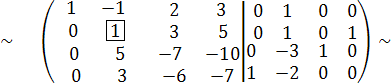
С1 := С2 + С1, С3 := -5∙С2 + С3, С4 := -3С2 + С4,

С1 := 5С3 + 22С1, С2 := 3∙С3 + 22С2, С4 :=- 15∙С3 +22∙ С4,
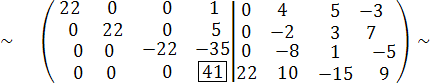
С1 :=- С4 +41С1, С2 := -5∙С4 + 41С2, С3 :=35∙С4 +41∙ С3
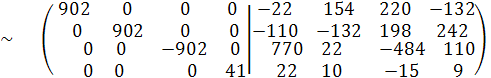
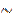
Разделив первую и вторую строки матрицы на 902, третью на -902.а четвертую на 41, получим
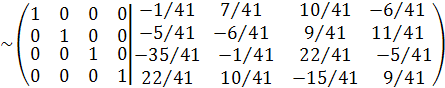
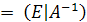 ,
,
А-1 = 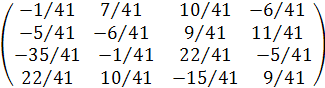 .
.
Задание №3
Найти фундаментальную систему решений.
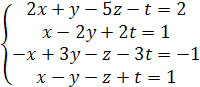 .
.
Решение. Составим расширенную матрицу и приведем ее с помощью элементарных преобразований к треугольному виду.


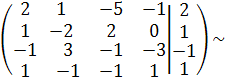 С2 С1
С2 С1 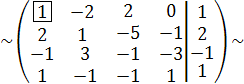
С2 := -2∙С1 + С2, С3 := С1 + С3, С4 := -С1 + С4

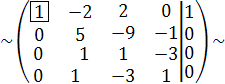
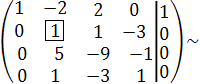
С3 := -5С2 + С3, С4 := -С1 + С4
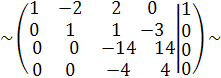
Разделим третью строку на 14, а четвертую на 4
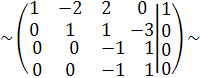 С4 := -С3 + С4
С4 := -С3 + С4 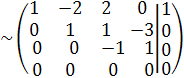
Составим по полученной матрице систему уравнений
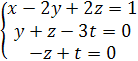 или
или 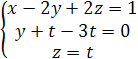 либо
либо 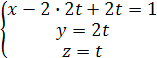 .
.
Таким образом, имеем 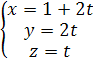 .
.
Обозначим t = С. Тогда система имеет множество решений :
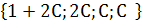 . При С = 1 получим ФСР, т.е.
. При С = 1 получим ФСР, т.е.
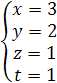
или 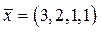 .
.
Задание №1
1.Даны матрицы
А =  и В =
и В = 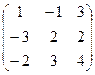 .
.
Вычислить А2 + ВА+2В.
2.Даны матрицы
А = 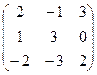 и В =
и В = 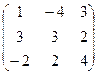 .
.
Вычислить А2 + АВ-3В.
3.Даны матрицы
А = 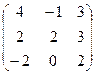 и В =
и В = 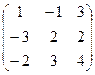 .
.
Вычислить В2 + АВ-3А.
4.Даны матрицы
А = 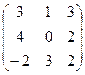 и В =
и В = 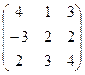 .
.
Вычислить В2-3В + ВА.
5.Даны матрицы
А = 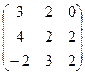 и В =
и В = 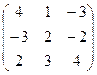 .
.
Вычислить В2+2А + ВА.
6.Даны матрицы
А = 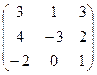 и В =
и В = 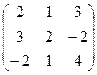 .
.
Вычислить 2А2-3В + ВА.
7.Даны матрицы
А = 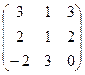 и В =
и В = 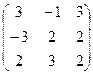 .
.
Вычислить В2-2В + 3ВА.
8.Даны матрицы
А = 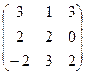 и В =
и В = 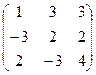 .
.
Вычислить В2-3В +2 АВ.
9.Даны матрицы
А = 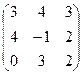 и В =
и В = 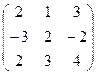 .
.
Вычислить 2А2-3В + ВА.
10.Даны матрицы
А = 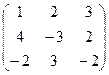 и В =
и В = 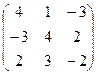 .
.
Вычислить В2-4А + ВА.
Задание №2
Решить системы линейных алгебраических уравнений
а) методом Гаусса;
б) по правилу Крамера;
в) матричным способом.
1. 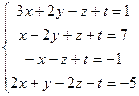 6.
6. 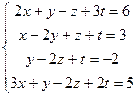
2. 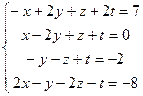 7.
7. 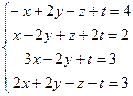
3. 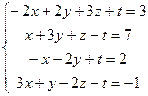 8.
8. 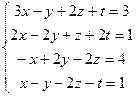
4. 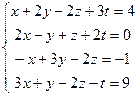 9.
9. 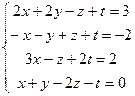
5. 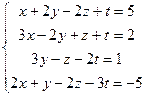 10.
10. 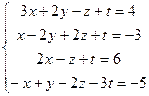
Задание №3
Решить систему линейных алгебраических уравнений
а) методом Гаусса;
1.  2.
2. 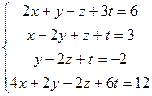
3. 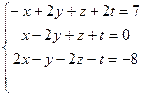 4.
4. 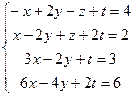
5. 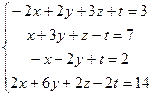 6.
6. 
7. 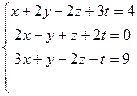 8.
8. 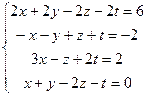
9. 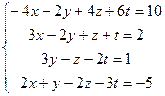 10.
10. 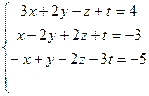
Задание №4
Найти собственные числа и собственные векторы матрицы А.
1. 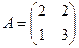
2. 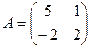
3. 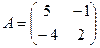
4. 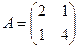
5. 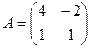
6. 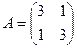
7. 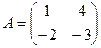
8. 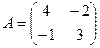
9. 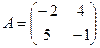
10. 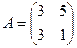
Рекомендуемая литература
1.Кострикин А.И.Введение в алгебру/А.И..Кострикин.-М.:Наука,1977.
2.Ефимов Н.В. Квадратичные формы и матрицы/Н.В.Ефимов.-Наука,1964.
3.Гельфанд И.М. Лекции по линейной алгебре / И.М.Гельфанд .- Наука,1971.
3.Карасев А.И.,Аксютина З.М.,Савельева Т.И.Курс высшей математики для экономических вузов.Ч.I,II /А.И . Карасев. , З.М.Аксютина, Т.И.Савельева – М.:Высш.школа,1982.
4.Бугров Я.С., Никольский С.М.Элементы линейной алгебры и аналитической геометрии/ Я.С Бугров, С.М.Никольский.- М.:Наука,1984.
5.Шипачев В.С. Высшая математика./В.С. Шипачев.- М.: Высшая школа,1985.
6.Данко П.Е., Попов А.Г.,Кожевников Г.Я.Высшая математика в упражнениях и задачах./ П.Е. Данко., А.Г .Попов., Г.Я. Кожевников –М.:Высш.школа,1986.
7.Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры/-М:Высш.школа,1998.
8.Зубков А.Н .Роль математики в формировании общекультурных и профессиональных качеств при подготовке современных специалистов в техническом
ВУЗе./ А.Н Зубков .- г.Таганрог. Аспекты модернизации образования и развития промышленности. Материалы VIII региональной научнот-пракической конференции учреждений высшего и профессионального образования,2010,с.69-72.
