Дифференциальные уравнения второго порядка
Определение: Уравнение вида
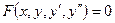 , , | (8.5.1) |
где 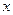 – независимая переменная,
– независимая переменная, 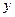 – искомая функция,
– искомая функция, 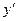 и
и 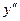 – соответственно ее первая и вторая производные, называется дифференциальным уравнением второго порядка.
– соответственно ее первая и вторая производные, называется дифференциальным уравнением второго порядка.
Примеры дифференциальных уравнений второго порядка:
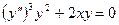 ,
, 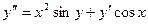 ,
, 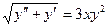 .
.
Будем рассматривать уравнения, разрешенные относительно 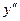 :
:
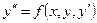 . . | (8.5.2) |
Уравнение (8.5.2) называется уравнением второго порядка, разрешенным относительно второй производной. В дальнейшем мы будем рассматривать уравнения второго порядка именно такого вида.
Как и в случае уравнения первого порядка, решением дифференциального уравнения второго порядка называется функция 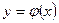 , определенная на некотором интервале
, определенная на некотором интервале 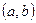 , которая при подстановке уравнение (8.5.2) обращает его в тождество. График решения называется интегральной кривой. Имеет место Теорема о существовании и единственности решения уравнения второго порядка.
, которая при подстановке уравнение (8.5.2) обращает его в тождество. График решения называется интегральной кривой. Имеет место Теорема о существовании и единственности решения уравнения второго порядка.
Теорема (Теорема Коши).
Пусть дано дифференциальное уравнение (8.5.1). Если функция 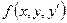 и ее частные производные
и ее частные производные 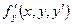 и
и 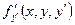 непрерывны в некоторой области
непрерывны в некоторой области 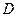 пространства переменных
пространства переменных 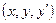 , тогда для любой внутренней точки
, тогда для любой внутренней точки 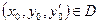 найдется единственное решение уравнения (8.5.1), удовлетворяющее условиям
найдется единственное решение уравнения (8.5.1), удовлетворяющее условиям 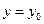 ,
, 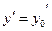 при
при 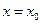 .
.
Геометрический смысл теоремы Коши заключается в том, что через заданную точку 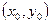 плоскости
плоскости 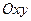 проходит единственная интегральная кривая с заданным угловым коэффициентом
проходит единственная интегральная кривая с заданным угловым коэффициентом 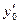 касательной.
касательной.
Условия, которые задают значение функции 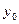 и ее первой производной
и ее первой производной 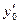 в фиксированной точке
в фиксированной точке 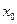 , называются начальными условиями (или условиями Коши) и записываются в такой форме:
, называются начальными условиями (или условиями Коши) и записываются в такой форме:
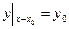 , , 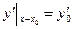 . . | (8.5.3) |
Задача нахождения решения уравнения (8.5.2), удовлетворяющего условию (8.5.3), называется задачей Коши для уравнения второго порядка.
Определение: Общим решением уравнения (8.5.2) называется функция 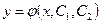 , удовлетворяющая этому уравнению при любых значениях констант
, удовлетворяющая этому уравнению при любых значениях констант 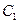 и
и 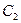 .
.
Определение
Частным решением уравнения (8.5.1) в области 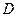 называется функция
называется функция 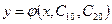 , полученная при фиксированных значениях постоянных
, полученная при фиксированных значениях постоянных 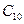 и
и 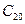 .
.
Рассмотрим для примера уравнение 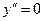 . Его общее решение получается при двукратном интегрировании уравнения
. Его общее решение получается при двукратном интегрировании уравнения 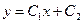 . Это решение представляет собой семейство прямых в произвольных направлениях, причем через каждую точку области
. Это решение представляет собой семейство прямых в произвольных направлениях, причем через каждую точку области  проходит бесконечное число таких прямых. Следовательно, для выделения частного решения, проходящего через заданную точку
проходит бесконечное число таких прямых. Следовательно, для выделения частного решения, проходящего через заданную точку 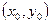 , необходимо задать еще и угловой коэффициент прямой, совпадающий в данном случае со своей касательной. Например, найдем частное решение , удовлетворяющее начальным условиям
, необходимо задать еще и угловой коэффициент прямой, совпадающий в данном случае со своей касательной. Например, найдем частное решение , удовлетворяющее начальным условиям
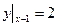 ,
, 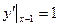 ,
,
т.е. нужно найти прямую, проходящую через точку 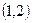 с угловым коэффициентом, равным единице. Подстановка начальных условий в общее решение уравнения приводит к системе двух линейных уравнений относительно постоянных
с угловым коэффициентом, равным единице. Подстановка начальных условий в общее решение уравнения приводит к системе двух линейных уравнений относительно постоянных 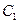 и
и 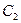 :
:
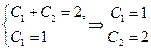 .
.
Таким образом, искомое частное решение этого уравнения при заданных начальных условиях это прямая 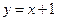 .
.
Уравнения, допускающие понижение порядка
Существуют три вида уравнения 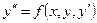 , которые путем замены переменной (искомой функции) сводятся к уравнениям первого порядка.
, которые путем замены переменной (искомой функции) сводятся к уравнениям первого порядка.
Уравнение вида
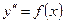 . . | (8.5.4) |
Ведем новую функцию 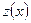 путем замены
путем замены 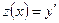 . Тогда исходное уравнение второго порядка преобразуется в неполное уравнение первого порядка:
. Тогда исходное уравнение второго порядка преобразуется в неполное уравнение первого порядка: 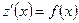 , решением которого является функция
, решением которого является функция 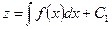 . Так как
. Так как 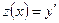 , то повторным интегрированием находим общее решение уравнения (8.5.4):
, то повторным интегрированием находим общее решение уравнения (8.5.4):
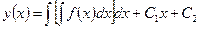 , , | (8.5.5) |
где 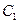 и
и 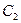 – произвольные постоянные.
– произвольные постоянные.
Уравнение вида
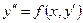 , , | (8.5.6) |
т.е. уравнение не содержит в явном виде 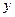 . Как и в предыдущем случае, положим
. Как и в предыдущем случае, положим 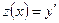 . Тогда получаем уравнение первого порядка общего вида
. Тогда получаем уравнение первого порядка общего вида 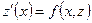 . Найдя общее решение этого уравнения
. Найдя общее решение этого уравнения 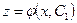 , повторным интегрированием получим искомое общее решение уравнения (8.5.6):
, повторным интегрированием получим искомое общее решение уравнения (8.5.6):
 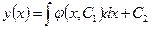 . . | (8.5.7) |
Уравнение вида
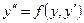 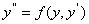 , , | (8.5.8) |
т.е. уравнение не содержит независимой переменной 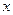 . Введем новую функцию, независящую от
. Введем новую функцию, независящую от 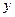 , полагая
, полагая 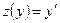 . Тогда (по правилу дифференцирования сложной функции)
. Тогда (по правилу дифференцирования сложной функции)
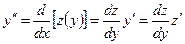 .
.
Уравнение (8.5.8) преобразуется в дифференциальное уравнение первого порядка относительно функции 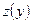 :
: 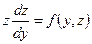 .
.
Пусть общее решение этого уравнения 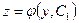 . Тогда обратной заменой получаем неполное уравнение первого порядка относительно функции
. Тогда обратной заменой получаем неполное уравнение первого порядка относительно функции 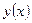 :
: 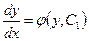 ,
,
из которого методом разделения переменных получаем функциональное соотношение для определения общего решения уравнения (8.5.8): 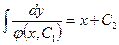 .
.
Рассмотрим примеры решения дифференциальных уравнений второго порядка.
Пример
Найти решение уравнения 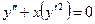 .
.
Решение
Это уравнение вида (8.5.6), поскольку оно не содержит в явном виде 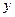 . Заменой
. Заменой 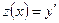 приведем его к уравнению первого порядка
приведем его к уравнению первого порядка 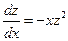 , откуда
, откуда 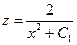 или
или 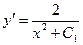 . Интегрируя это уравнение, получаем общее решение исходного уравнения:
. Интегрируя это уравнение, получаем общее решение исходного уравнения: 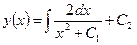 . В зависимости от выбора знака
. В зависимости от выбора знака 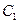 интеграл в правой части этого равенства может быть равен:
интеграл в правой части этого равенства может быть равен: 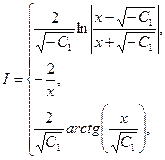
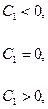
Пример
Найти решение уравнения 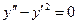 .
.
Решение:
Это уравнение вида (8.5.8), поскольку оно не содержит в явном виде 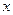 . Заменой
. Заменой 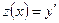 приведем его к уравнению первого порядка
приведем его к уравнению первого порядка  .
.
Первое решение этого уравнения 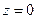 или
или 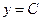
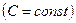 . Сокращая обе части этого уравнения на
. Сокращая обе части этого уравнения на 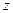 , получим
, получим 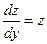 . Общее решение этого уравнения
. Общее решение этого уравнения 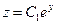 .
.
Наконец, обратная замена приводит к уравнению первого порядка 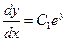 . Общее решение этого уравнения есть функция
. Общее решение этого уравнения есть функция 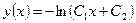 .
.
Нетрудно видеть, что это решение включает в себя и решение 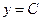 (при
(при 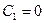 ,
, 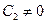 ).
).
Линейные дифференциальные уравнения второго порядка
Определение
Дифференциальное уравнение вида
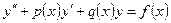 . . | (8.5.9) |
где 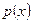 ,
, 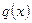 и
и 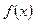 – функции, непрерывные на некотором интервале
– функции, непрерывные на некотором интервале 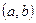 называется линейным дифференциальным уравнением второго порядка.
называется линейным дифференциальным уравнением второго порядка.
Если 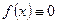 , то уравнение (8.5.9) называется линейным однородным уравнением, если же
, то уравнение (8.5.9) называется линейным однородным уравнением, если же 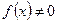 , то уравнение (8.5.9) называется линейным неоднородным уравнением.
, то уравнение (8.5.9) называется линейным неоднородным уравнением.
Если разрешить уравнение (8.5.9) относительно второй производной, то легко увидеть, что оно является частным случаем уравнения (8.5.2) и удовлетворяет условиям теоремы Коши. Поэтому для любых начальных условий (8.5.3) при 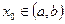 это уравнение имеет единственное решение задачи Коши.
это уравнение имеет единственное решение задачи Коши.
Линейные однородные уравнения второго порядка
Рассмотрим свойства решений линейных однородных дифференциальных уравнений второго порядка:
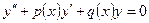 . . | (8.5.10) |
Теорема
Пусть функции 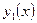 и
и 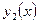 – решения уравнения (8.5.10). Тогда функция
– решения уравнения (8.5.10). Тогда функция 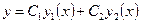 также является решением этого уравнения при любых постоянных
также является решением этого уравнения при любых постоянных 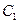 и
и 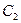 .
.
Напомним, что линейной комбинацией функций 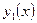 и
и 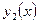 с коэффициентами
с коэффициентами 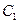 и
и 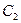 называется выражение вида
называется выражение вида 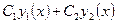 .
.
Если линейная комбинация функций 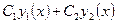 равна нулю тогда и только тогда, когда
равна нулю тогда и только тогда, когда 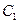 и
и 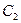 равны нулю, то функции
равны нулю, то функции 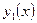 и
и 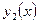 являются линейно независимыми, в противном случае функции
являются линейно независимыми, в противном случае функции 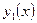 и
и 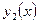 – линейно зависимые.
– линейно зависимые.
Пример
Доказать, что следующие функции линейно независимы:
А) 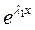 и
и 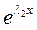 , где
, где 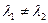 ,
,
Б) 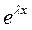 и
и 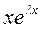 ;
;
В) 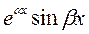 и
и 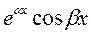 , где
, где 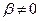 .
.
