Уравнения и неравенства с модулем
Свойства модуля:
1) 
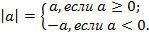
Противоположные числа – числа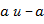 
, имеющие одинаковый модуль (говорят, что числа 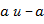равны по модулю).
Геометрический смысл: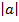 
– расстояние от точки с координатой 
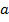до точки с координатой 0. 
2) 
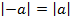(модули противоположных чисел равны). Аналогично и для выражений, например 
.
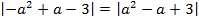3) 
.
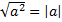Помните, модуль числа – число положительное или 0! Так, например,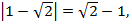 
, 
.
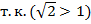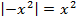Подходы к решению уравнений и неравенств:
1) 1 или 2 модуля: раскрытие по определению.
Пример 1.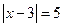 
.
Решение:
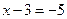или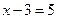 
.
.
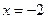
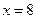Ответ: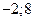 
.
Пример 2.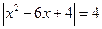 
.
Решение:
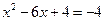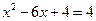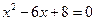
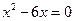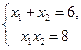
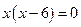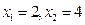
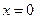или 
.
.
.
или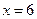 
.
Ответ: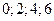 
.
Пример 3.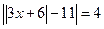 
.
Решение:
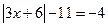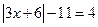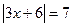
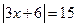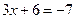или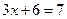 
.
.
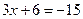или 
. 
или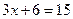 
.
. 
.
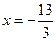
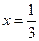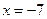
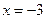Ответ: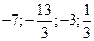 
.
Пример 4.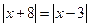 
.
Решение:
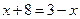или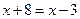 
.
.
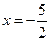
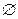Ответ: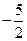 
.
Пример 5.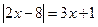 
.
Решение:
Т.к. слева стоит модуль, то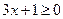 
(*).
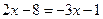или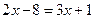 
.
.
.
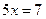
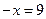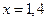
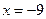Второй корень является посторонним, т.к. не удовлетворяет (*).
Ответ: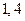 
.
Пример 6.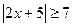 
.
Решение:
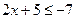или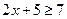 
.
.
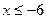
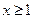Ответ: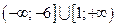 
.
Пример 7.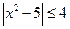 
.
Решение:
.
.
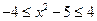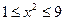Поскольку каждая часть неравенства положительна, можем извлечь корень:
.
,
.
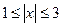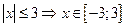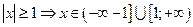Объединяя полученные решения, получим ответ.
Ответ: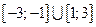 
.
Пример 8.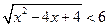 
.
Решение:
.
.
.
.
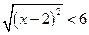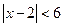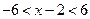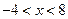Ответ: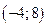 
.
Пример 9.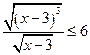 
.
Решение:
ОДЗ: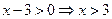 
(стоит под корнем в знаменателе).
Используя свойство квадратного корня, исходное неравенство примет вид:
.
.
.
.
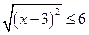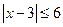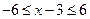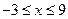Ответ: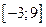 
.
Пример 10.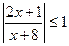 
.
Решение:
.
.
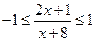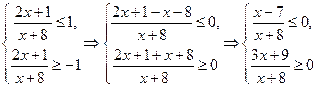Последние неравенства решаем по методу интервалов:
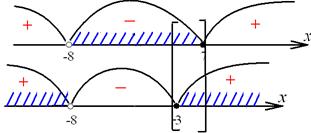
Ответ: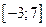 
.
2) Несколько модулей: интервальное раскрытие.
На ЦТ такого задания быть не должно,пример рассматривается в ознакомительных целях.
Пример 11. 3|x – 1| – 2|x – 2| + |x + 3| = 2.
Решение:
Находим нули подмодульных выражений:
.
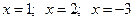Т.о., имеется 4 интервала, на каждом из которых подмодульные выражения или >0 (‘+’) или <0 (‘–‘):
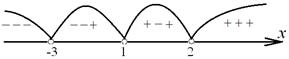
(знаки расставлены в порядке следования модулей)
Деление на интервалы (включение/невключение в интервал нулей) условное:
1) 
: 
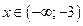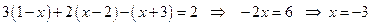. Данное решение не принадлежит рассматриваемому интервалу, но не волнуйтесь: оно будет решением следующего интервала.
2) 
: 
.
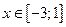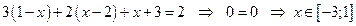3) 
: 
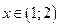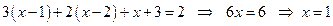(не принадлежит рассматриваемому интервалу).
4) 
: 
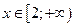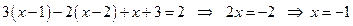(не принадлежит рассматриваемому интервалу).
О т в е т: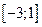 
.
3) Уравнения и неравенства с одинаковыми компонентами.
A. Метод замены переменных.
Пример 12.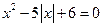 
.
Решение:
Пусть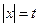 
, тогда 
.
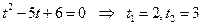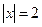или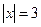 
.
Ответ: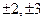 
.
Пример 13.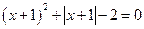 
.
Решение:
Пусть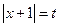 
, тогда 
.
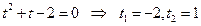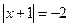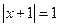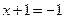или 
.
или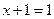 
.
.
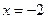
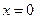Ответ: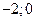 
.
Б. Используются свойства модуля.
Пример 14. Решите уравнение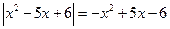 
.
Решение:
Перепишем уравнение в виде: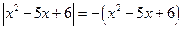 
.
Получается, что модуль выражения равен этому выражению, взятому с противоположным знаком. Такое возможно только в том случае, если данное выражение отрицательно или равно нулю:
.
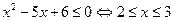Ответ: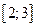 
.
Пример 15. Решите неравенство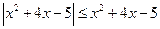 
.
Решение:
Модуль A не может быть меньше A, возможно только равенство, из которого делаем вывод:
.
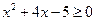Ответ: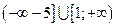 
.
Пример 16. Решите неравенство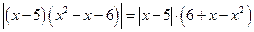 
.
Решение:
Перепишем уравнение в виде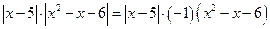 
.
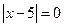или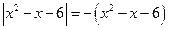 
.
.
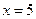
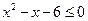Ответ: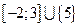 
.
В. Используются свойства других функций.
Пример 17. Решите уравнение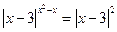 
.
Решение:
Возможны следующие случаи:
1) х2 – х = 2 (степени равны), откуда х1 = 2, х2 = –1.
2) 0а = 0в, а > 0; в > 0, т.е. |х – 3| = 0, х3 = 3.
3) |х – 3| = 1, откуда х4 = 4; х5 = 2.
Ответ:–1; 2; 3; 4.