Условия нахождения экстремума функции

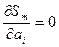
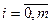
Условие минимума: 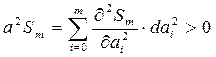,т.е. второй дифференциал >0.

Т. о. условие экстремума дает систему m+1 уравнений m+1 неизвестными

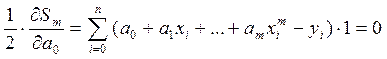
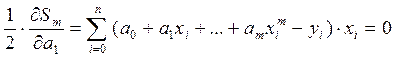(3)

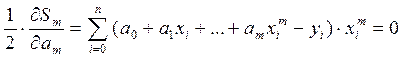
Введем обозначения:

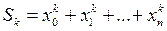
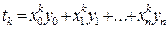k=(0,1,2)

Например: k=1;

тогда S₁ = х₀+ х₁+…+ х_n

t₁ = х₀y₀+ х₁ y₁+…+ х_n y_n

t₀ = х₀⁰ y₀+ х₁⁰ y₁+…+ х_n⁰ y_n =Σy_i

S₀= х₀⁰ + х₁⁰ +…+ х_n⁰ =1+1…1 = n+1

Тогда система (3) примет вид:

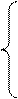
a₀ s₀ + a₁ s₁ + a₂ s₂ +…+ a_m s_m = t₀

a₀ s₁ + a₁ s₂ + a₂ s₃ +…+ a_m s_m+1 = t₀ (4)

a₀ s₂ + a₁ s₃ + a₂ s₄+…+ a_m s_m+2 = t₀

a₀ s_m + a₁ s_m+1 + a₂ s_m+2 +…+ a_m s_2m = t₀

где S₀ = n+1.

Если среди точек x_0, х_1,…, х_n нет совпадающих и m≤n, то определитель системы (4) отличен от нуля и система имеет единственное решение a₀=a₀٭,a₁=a₁٭,…,a_m=a_m٭

Полином (1) с таким коэффициентом будет обладать минимальным среднеквадратичным отклонением S_min.

Если m=n, то Q_m(x) совпадает с полиномом Лагранжа

(т.е. будет решаться задача интегрирования) и S_min=0.

,то аппроксимирования функций – более общий процесс, чем интерполирование.

Пример: подобрать аппроксимирующий полином второй степени

y = a₀+a₁x+a₂x² для данных:

х	0,78	1,56	2,34	3,12	3,81
y	2,5	1,2	1,12	2,25	4,28

m = 2

n = 4 (n+1=5)

Cтроим таблицу

X0	X	X2	X3	X4	Y	XY	X2Y
	0,78	0,608	0,475	0,37	2,5	1,95	1,52
	1,56	2,434	3,796	5,922	1,2	1,872	2,921
	2,34	5,476	12,813	29,982	1,12	2,621	6,133
	3,12	9,734	30,371	94,759	2,25	7,02	21,902
	3,81	14,516	55,306	210,717	4,28	16,307	62,28
S	11,61	32,768	102,761	341,75	11,35	29,77	94,604

Cоставляем уравнения для коэффициентов а₀,а₁,а₂ :

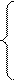5 a₀ + 11.61 a₁ + 32.768 a₂ = 11.350

11.61 a₀ + 32.768 a₁ + 102.761 a₂ = 29.770 (5)

32.768 a₀ + 102.761 a₁ + 341.750 a₂ = 94.604

Решая систему (S) получаем:

а₀=5.045; а₁=4.043; а₂=1,009.

Т.е. у = 5.045 – 4.043 х + 1.009 х²

Сопоставим некоторые значения Y_i с вычисляемыми (6)

X	Y	Y	ε=Y-Y
0,78	2,5	2,505	0,005
1,56	1,2	1,194	-0,006
2,34	1,12	1,11	-0,01
3,12	2,25	2,252	0,002
3,81	4,28	4,288	0,008

|ε|_max=0.01

Удобнее пользоваться при оценке «качества» приближения не таблицей, а одним показателем – среднеквадратической нормой.

d (f, Q_m) = ( 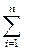[f (x_i) – Q_m(x_i)] ²)^1/2

Или величиной

∂ (f, Q_m) = d (f, Q_m)/ ║f║, где ║f║ - норма функции;

║f║ =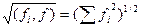

В нашем случае: d = 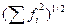≈15*10^-3 (0.015)

Еще более удобный показатель – относительное среднеквадратическое отклонение ∂

∂(f, Q_m) = d (f, Q_m)/ ║f║ - безразмерная величина.

В нашем случае ║f║ = =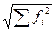

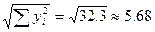
∂(f, Q_m) ≈2,6*10^-3 = 0,0026

Правильнее было бы называть среднеквадратическим отклонением величину

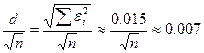
Мы рассмотрели приближение функции обычным полиномом. Рассмотрим теперь аппроксимацию обобщенным полиномом.

Q_m (х)=C₀φ₀ (x)+C₁φ₁ (x) +...+ C_mφ_m (x).

Теперь необходимо минимизировать сумму квадратов

_n

S_m=Σ [C₀φ₀ (x_і) + C₁φ₁ (x_і) +...+ C_mφ_m (x_і) – f (x_і)]²

^і=0

Условия экстремума дают систему уравнений

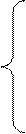
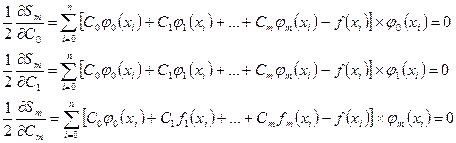(7)

_n

Введем обозначения: (φ,ψ) = Σ φ (x_і) × ψ (x_і)

^і=0

Тогда (7) примет вид:

C₀ (φ₀, φ₀) + C₁ (φ₁, φ₀) +…+ C_m (φ_m, φ₀) = (f, φ₀)

C₀ (φ₀, φ₁) + C₁ (φ₁, φ₁) +…+ C_m (φ_m, φ₁) = (f, φ₁) (8)

C₀ (φ₀, φ_m) + C₁ (φ₁, φ_m) +…+ C_m (φ_m, φ_m) = (f, φ_m)

Из этой системы определяют коэффициенты C₀, C₁,…, C_m.

ЛЕКЦИЯ 16

. Функции, ортогональные на точечном множестве.

Функции φ (x) и ψ (x) называют ортогональными на множестве

точек x = {x₀, x₁, x₂,…, x_n}, если

_n

Σ φ (x_і) × ψ (x_і) = 0.

^і=0

Пример: φ (x) = 3x² - 15x + 10; ψ (x) = 2x – 5

ортогональны на множестве x_і = і (і = 0,1,2,3,4,5).

Имеем: φ (0) = 10;

x
φ		-2	-8	-8	-2
ψ	-5	-3	-1
φ × ψ	-50			-8	-6		Σ = 0

Система функций {φ_k (x)} называется ортогональной на данном множестве X, если функции

системы попарно ортогональны между собой на этом множестве X.

Функция φ(x)≡0, естественно, ортогональна любой функции. Поэтому будем рассматривать только такие функции,

_n

Σ φ² (x_і) > 0

^і=0

т.е. хотя бы одно значение φ (x_і) ≠ 0

Система ортогональных функций {φ_k (x)} называется ортонормированной, если для всех k

выполнено равенство

║φ_k (x)║ = 1, где 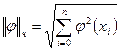- норма функции φ(х)

Если {φ_k (x)} – система функций ортогональна на множестве Х, то система функций

{φ_k (x) ⁄ ║φ_k║_х} – ортогональная на Х.

Функции f_k (x) (k = 0, 1,…,m) называются линейно независимыми на множестве Х, если они

определены на этом множестве и из равенства

λ₀f₀ (x_і) + λ₁f₁ (x_і) +…+ λ_mf_m (x_і) = 0 (і = 1, n)

Следует, что все постоянные λ_k = 0 (k = 0,m)

В противном случае функции f_k (x) – линейно зависимые на Х.

Если множество Х не точечное, а континумум, т.е. х принадлежит отрезку a < х < b, то условие линейной независимости то же самое, только рассматриваются не точки x_і, а множество х ? (a, b), т.е. рассматриваем условие

_m

Σ λ_kf_k (x) = 0 х ? (a, b)

^k=0

Легко можно доказать лемму:

Функции φ_k (x) (k = 0, 1,…,m), ортогональные на множестве Х = {x₀, x₁, x₂,…,x_m} и имеющие ненулевые нормы, линейно независимы на этом множестве.

Рассмотрим систему полиномов

P₀ (x), P₁ (x),…, P_m (x), (1)

ортогональны на точечном множестве Х = {x₀, x₁,…,x_n}, т.е.

_n

Σ P_і (x_і) P_k (x_і) = 0 при j ≠ k (2)

^і=0 _{2 n 2}

и таких, что S_j = ║P_j║ = Σ P_j (x_і) > 0 – квадрат нормы

^{x і=0}

Пусть степень полинома P_j = j

Т.к. полином P_і (x) (j = 0, 1, 2,…,m) линейно независимые на Х поскольку они ортогональны, то любой полином Q_m (x) степени не выше m может быть представлен в виде линейной комбинации полиномов (2), т.е.

Q_m (x) = b₀ P₀ (x) + b₁P₁ (x) +…+ b_mP_m (x) (3),

где b_і (i = 0,m) – некоторые постоянные числа.

Выражение (3) называется разложением полинома Q_m (x) по системе (1)

Если полином P_j (x) ортогональны, то коэффициенты b_k равны

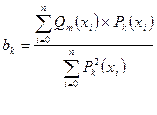k = 0, 1,…,m (4)

Действительно, умножим (3) на полином P_k (x) (k ≤ m) и просуммируем результат по всем x_i

(i = 0,n)

_{n n n n 2 n}

Σ Q_m (x_i) × P_k (x_i) = b₀ Σ P₀ (x_i) × P_k (x_i) + b₁ Σ P₁ (x_i) × P_k (x_i) +...+ b_k Σ P_k (x_i) +...+ b_m Σ P_m (x_i) ×

^{і=0 і=0 і=0 і=0 і=0}

× P_k (x_i) (5)

В силу условия ортогональности из (5) следует (4), т.к. все Σ P_j (x) × P_k (x) = 0 для j≠k

Коэффициенты (4) называют коэффициентами Фурье полинома Q_m (x) относительно данной системы функций P_k (x) (k = 0,m), ортогональных на Х.

_n

Если система (1) ортогональна на Х, т.е. Σ Q_m (x_i) × P_k (x_i) (6)

^і=0

Теперь будем аппроксимировать заданную функцию y = f (х) полиномом Q_m (x) на множестве Х.

Q_m (x) = C₀P₀ (x) + C₁P₁ (x) +…+ C_mP_m (x),

где {P_k (x)} (k = 0,m), - ортогональные полиномы.

_{n 2}

Минимизируя S _m = Σ [C₀P₀ (x_i) + C₁P₁ (x_i) +…+ C_mP_m (x_i) - f (х_i)] ­по C₁, C₂,…, C_m, т.е. приравнивая

^і=0

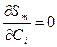
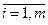и разрешая полученную систему уравнений, получим:

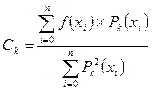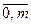k= (7)

C_k – коэффициенты Фурье функции f (x) относительно ортогональной системы {P_k (x)} на Х

Беря вторую производную 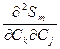, можно убедиться, что 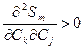и, следовательно

C_m (C_k) – минимальна!

Т.о.

Обобщенный полином фиксированного порядка m с коэффициентами Фурье данной функции f (х) на множестве Х = {x₀, x₁,…,x_n} – полином Фурье - обладает наименьшим квадратичным отклонением от этой функции на Х по сравнению со всеми полиномами того же порядка m.

Можно показать, что для полинома Фурье

_{2 m 2 2}

S_{m =} ║f (х)║ - Σ C_k × ║P_k║

^{k=0 x}

_{2 2 m n}

Если система {P_k (x)} ортонормирована, то ║P_k║ = 1 и S_{m =} ║f (х)║ - Σ C_{k ,} C_{k =} Σ f (х_i) × P_k (х_i)

^{х k=0 і=0}

III. Полиномы Чебышева, ортогональные на системе равноотстоящих точек.

Пусть дана система n + 1 равноотстоящих точек х = {x₀, x₁,…,x_n} с шагом n. С помощью

линейного преобразования 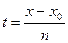переведем эти точки в t = 0, 1, 2,…, n.

Полиномы P_{0, n} (t), P_{1, n} (t),…, P_{m, n} (t) (m ≤ n) степеней 0, 1,…, m, ортогональные на множестве {0, 1, 2,…,n} и отличные от нуля на этом множестве, называются ортогональными полиномами Чебышева.

(P_{k, n} (t) : k – степень полинома, n – число точек, уменьшенное на 1)

Полиномы Чебышева можно задать формулой

k s s s t^[s]____ (1)

P_{k, n} (t) = Σ (-1) C C ×

^{S = 0 k k k + s} n^[s]

где k = 0, 1,…, m;

s

C - число сочетаний из k по s

^k

t^[s] = t × (t - 1) × (t - 2) ×...× (t-s +1)

обобщенные степени t и n

n ^[s] = n × (n - 1) × (n - 2) ×...× (n – s+1)

Т.о. четыре первых ортогональных полинома равны:

P_{0, n} (t) = 1

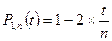; (n≥1) 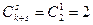, k=1, s=1

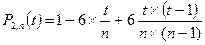; (n≥2) (2)

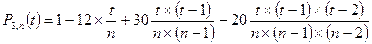; (n≥3)

Возвращаясь к прежней переменной х, получим систему полиномов, ортогональных на множестве Х

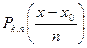, (k=0,1,…,m; m≤n)

Можно показать, что квадрат нормы полинома 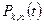равен

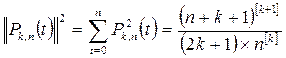^{(3) [n+k+1], [k+1] – обобщенные степени}

Разделив многочлены 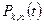на их нормы, мы получим нормированную систему ортогональных полиномов Чебышева

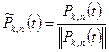(k=0,1,2,…,m; m≤n) (4)

Пример. Получить систему полиномов до третьей степени включительно, ортонормированных на системе точек ; ; ; ; ;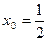

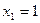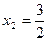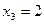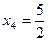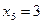
Решение. Полагая 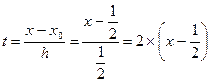, переведем точки 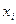в целочисленные точки t=0,1,2,3,4,5. Теперь в формулах (1) принимаем n=5.

Имеем ;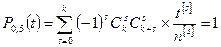

(k=0, n=s)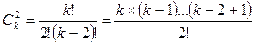

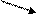
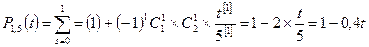
k=1, n=5 s=0 1 2 переходим к Х

1-0,4t=1-0,4*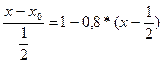

И т.д.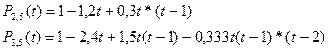

По формуле (3) вычисляем нормы 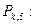по формуле (3) получаем квадрат нормы, затем вычисляем корень, т.е. норму!

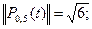
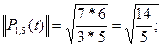
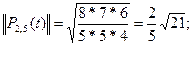
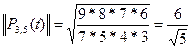
Делим полиномы 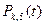на их нормы и переходим от переменной t к переменной х, получим нормированную систему ортогональных полиномов Чебышева:

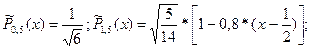
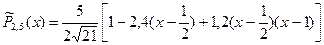
Если функция Y=f(x) задана на множестве узлов 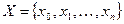с шагом h, то наилучший аппроксимирующий ее на Х полином степени m будет иметь вид:

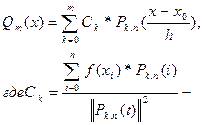
(5)

(k=0,1,2,…,m) (6)
-коэффициенты Фурье ф-ии f(x) относительно системы ортогональных полиномов Чебышева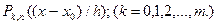

Из (5) и (6) следует, что полином 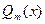не изменится, если ортогональные полиномы Чебышева 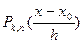умножить на постоянные множители, отличные от нуля. Т.к.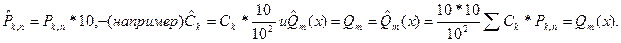

Поэтому часто вместо полиномов 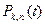пользуются полиномами 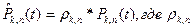подобраны так, чтобы для целочисленных значений аргумента t значения 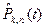тоже были целочисленными. Имеются (в справочной литературе) таблицы полиномов 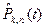, что значительно упрощает процедуры построения полиномов .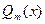