Численные методы безусловной оптимизации
I. Необходимые и достаточные условия экстремума в задачах безусловной оптимизации.
Пусть будет задано множество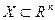 
и функция 
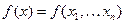определенная на этом множестве.
( 
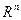- линейное, n – мерное пространство)
Точка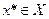 
называется точкой локального минимума функции 
на множестве х, если существует шар 
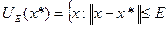такой, что для любого 
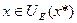выполняется неравенство:
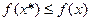(1)
Если неравенство выполняется как строгое (при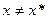 
), то говорят, что 
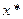- точка строгого локального минимума. Точка 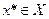называется точкой глобального минимума функции на множестве х, если неравенство (1) выполняется для любого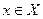 
.
Аналогично определяются точки локального и глобального максимума на множестве х.
Точки локального минимума и максимума функции называют точками экстремума этой функции.
Задача отыскания всех локальных минимумов (max) функции , если множество х совпадает со всем n-мерным пространством, т.е.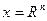 
, называют задачей безусловной оптимизации, а функция - целевой функцией.
Задачи оптимизации:
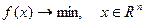(2)
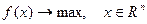(3)
Задача (3) эквивалентна задаче
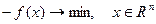
Теорема 1.
Пусть х* - точка локального минимума функции , которая имеет в этой точке непрерывные частые производные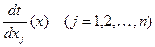 
, тогда частные производные функции в этой точке равны нулю, т.е.
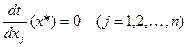
Иначе говоря, в точке экстремума градиент функции
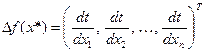
Равен нулевому вектору,
т.е.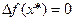 
Точка ч*, удовлетворяющая условию 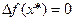, называется стационарной точкой функции .
Квадратная матрица А называется симметричной, если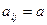 
. симметричная матрица А называется неотрицательно определенна, если для любого 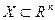скалярное произведение векторов 
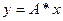и ч неопределенно; т.е. 
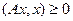; положительно определенной, если 
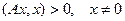; неопложительно определенной, если 
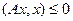; отрицательно определенной, если 
.
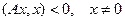Теорема 2. (критерий Сильвестра).
Симметричная матрица Ф неотрицательно (положительно) определена тогда и только тогда, когда все главные (угловые) миноры неотрицательны (положительны):
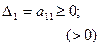
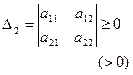и т.д.,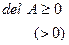 
Симметричная матрица А является неположительно (отрицательно) определенной тогда и только тогда, когда знаки последовательных гдавных миноров чередуются, причем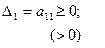 
; 
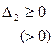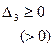и т.д.
Матрица вторых производных функции .
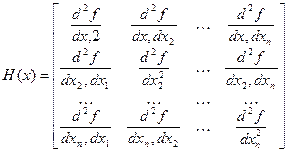
Называется матрицей Гессе функции .
Теорема 3.
Если точка х* - локальное решение задачи минимизации, и в этой точке имеет непрерывные частные производные до второго порядка включительно, то матрица Гесса функции в точке х* является неорицательно определенной, т.е.
.
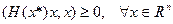Теорема 4. (о достоверных условиях локального экстремума).
Если точка х* является стационарной точкой функции , т.е.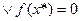 
и матрица Гессе функции в точке х* положительно определена, то х* - строгое локальное решение задачи (2)- минимизации.
Если точка х* является стационарной и матрица Гессе в ней отрицательно определена, то х* - строгое локальное решение задачи максимизации функции .
Для одномерной оптимизации
- условие стационарности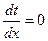 
.
- условие минимума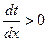 
.
(максимума)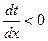 
.
Пример. Решить задачу.
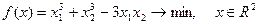
Решение. Находим стационарные точки :
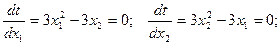
Система имеет два решения:
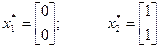
Матрица Гессе: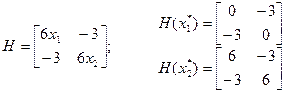 
Матрица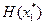 
не является неотрицательно определенной.
Матрица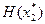 
- положительно определена.
В.т.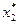 
- минимум функции.
II. Выпуклые множества и выпуклые функции
Множество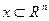 
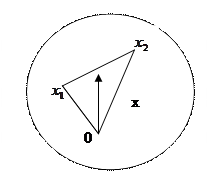
называется выпуклым, если вместе с любыми двумя точкам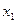и 
и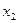 
ему целиком принадлежит отрезок, соединяющий эти точки.
Условия выпуклости:
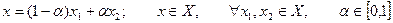(4)
Функция , определенная на выпуклом множестве 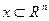, называется выпуклой, если 
.
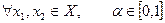Справедливо неравенство
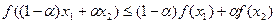(5)
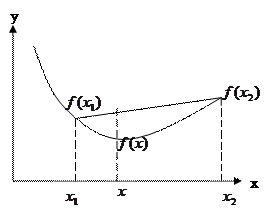
Если неравенство (S) – строгое, то функция строго выпуклая.
Теорема 5.
Если функция выпукла на множество Х и Х*.
Является стационарной точкой функции , т.е. 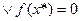, то х* - строгое локальное решение задачи.
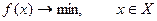(6)
Теорема 6.
Если функция и множество х выпуклы, то любое локальное решение задачи (6) является также глобальным решением на множество х.
Теорема 7. (достаточные условия выпуклости функции).
Если имеет непрерывные производные до 20го порядка включительно и матрица Гессе функции положительно определена в любой точке х выпуклого множества х, то является выпуклой на множестве х.
Пример.
Показать, что стационарная точка функции
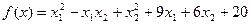
Является глобальным решением задачи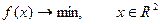 
.
Решение.
Находим стационарную точку функции :
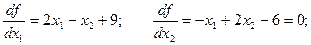
Точка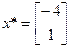 
- решение системы.
Находим матрицу Гессе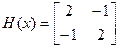 
.
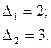
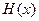положительно определена во всех точках выпуклого множества х (Н не зависит от х).
Точка х* - решение глобальной задачи минимизации.
Литература
- Б.П. Демидович, И.А. Марон. «Основы вычислительной математики»
М.: Наука, 1970, 664 с.
2. Н.В.Копченова, И.А. Марон
«Вычислительная математика в примерах и задачах».
М.: Наука, 1972, 367 с.
И.С. Березин, Н.П. Жидков. «Методы вычислений», т 1,т 2. М.: 1962
4. Р.В. Хемминг. «Численные методы для научных работников и инженеров» М.: Мир, , 1977
5. Б.П. Демидович, И.А. Марон, Э.З. Шувалова
«Численные методы анализа». М.: Наука 1967, 368 с.
6. В.И. Ракитин, В.Е. Первушин. «Практическое руководство по методам вычислений». М.: Высшая школа, 1998, 383 с.
7. М.Малькольм, К. Фоулер «Машинные методы математических вычислений». М.: Мир, 1980, 279 с.
8. С.В. Михайленко. «Численные методы (учебное пособие)». Харьков, из-во ХАИ, 1978, 126 с.
9. С.В. Михайленко. «Численные методы (учебное пособие по лабораторному практикуму)». Харьков, из-во ХАИ, 1978, 92 с.
10. Н.С. Бахвалов. «Численные методы». М.: СПб - 2000, 622 с.
11. Н.С. Бахвалов. «Численные методы в задачах и упражнениях». М.: Высшая школа - 2000, 622 с.