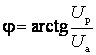Последовательное соединение R-L-C элементов
К цепи с последовательным соединением R, L, C приложено синусоидальное напряжение
u = Um×sin(ωt + yu).
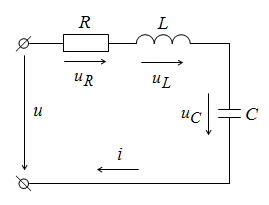
На основании II закона Кирхгофа можно записать u = uR + uL + uC.
Для yu = 0 можно записать:
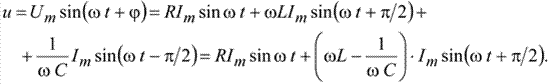 (2.22)
(2.22)
Кривые тока и напряжений изображены на рис. 2.9.
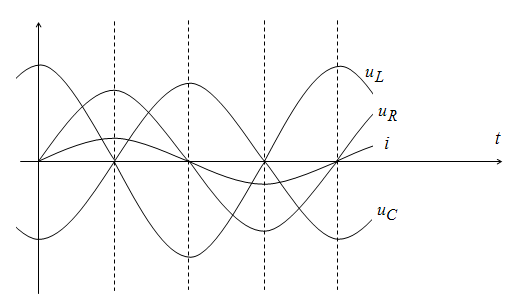
Рис. 2.9. Кривые тока и напряжений при последовательном соединении
Величина 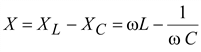 называется реактивным сопротивлением. В зависимости от знака она может иметь индуктивный (X > 0) или емкостной (X < 0) характер.
называется реактивным сопротивлением. В зависимости от знака она может иметь индуктивный (X > 0) или емкостной (X < 0) характер.
В комплексной форме уравнение (2.22) можно записать
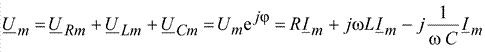
или
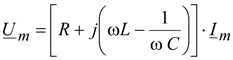 .(2.23)
.(2.23)
Это выражение, связывающее комплексы тока и напряжения, называют законом Ома в комплексной форме.
Отношение 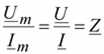 называется комплексным сопротивлением:
называется комплексным сопротивлением:
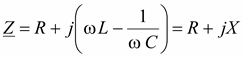 .
.
Действительная часть полного сопротивления – R называется активным сопротивлением, а мнимая – X – реактивным.
Для нахождения подводимого напряжения U и угла сдвига фаз φ можно воспользоваться векторной диаграммой, соответствующей уравнению (2.23).
На рис. 2.10 изображены векторы тока и напряжений цепи при индуктивном и емкостном характерах нагрузки. Из векторных диаграмм видно, что входное напряжение будет равно
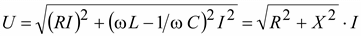 . (2.24)
. (2.24)
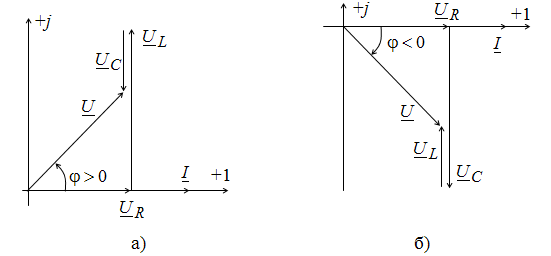
Рис. 2.10. Векторные диаграммы при индуктивном (а) и емкостном (б) характере нагрузки
Из закона Ома следует, что модуль полного сопротивления равен
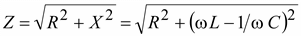 .(2.25)
.(2.25)
Угол фазового сдвига между током и напряжением равен
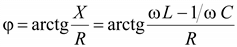 . (2.26)
. (2.26)
Если задано напряжение 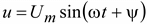 , то ток в последовательно соединенных элементах R, L, C будет равно
, то ток в последовательно соединенных элементах R, L, C будет равно
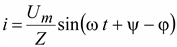 . (2.27)
. (2.27)
Угол φ положителен при индуктивном характере цепи, т.е. при X > 0, и отрицателен при емкостном (X < 0). На векторной диаграмме положительный угол φ отсчитывается от вектора тока к вектору напряжения против часовой стрелки.
При X = XL – XC = 0 ток совпадает по фазе с напряжением. Такой режим работы электрической цепи называется резонансом напряжений. Этот режим характеризуется потреблением только активной мощности. При этом ток в цепи максимален, и напряжения на реактивных элементах могут во много раз превышать входное напряжение (XL = XC >> R).
Из выражений (2.25) и (2.26) можно получить
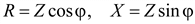 .(2.28)
.(2.28)
На рис. 2.11 изображены соответствующие треугольники сопротивлений.
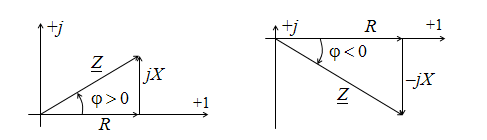
Рис. 2.11. Треугольники сопротивлений
Для характеристики катушек индуктивности пользуются понятием добротности катушки 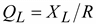 , которая равна тангенсу угла сдвига фаз φ. Чем ниже величина R, тем выше добротность катушки.
, которая равна тангенсу угла сдвига фаз φ. Чем ниже величина R, тем выше добротность катушки.
Умножив правые и левые части выражения (2.28) на I, получим
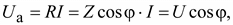
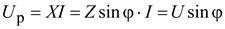 .
.
Если разложить напряжение на 2 составляющих, то получим треугольник напряжений.
Составляющая напряжения Ua, совпадающая с током по фазе, называется активной составляющей. Она определяет, какая часть напряжения
расходуется на выделение тепла. Составляющая Up, сдвинутая относительно
тока по фазе на 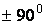 , называется реактивной и определяет интенсивность
, называется реактивной и определяет интенсивность
преобразования энергии источника в электромагнитную энергию полей.

Рисунок 2.9
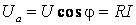 ,
, 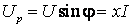 ,
, 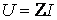 ;
; 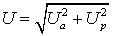 ;
;