Падение и потери напряжения в линии электропередач
Разность между напряжениями начала и конца линии называют падением напряжения, причем эта разность есть геометрическая.
На схеме замещения одной фазы электропередачи:
r – активное сопротивление провода ЛЭП.
х – реактивное сопротивление провода.
zн – комплексное сопротивление нагрузки (характеризуется углом φ).
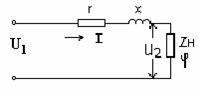
Считаем U2 - известно. Построим векторную диаграмму и найдем вектор U1.
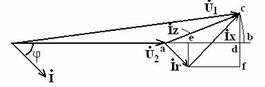
ас – падение напряжения.
аb – потеря напряжения.
На практике отрезок ad считают потерей напряжения, пренебрегая отрезком db.
ad=ae+eb - продольная слагающая падения напряжения (потеря).
ae=Ircosф ed=Ixsinф фазная потеря напряжения ΔUф=Ircosф+Ixsinф
Поперечная слагающая падения напряжения изображается отрезком cd:
сd=cf-df Ucd= Ircosф-Ixsinф
Модуль вектора напряжения в начале ЛЭП определяется по теореме Пифагора:
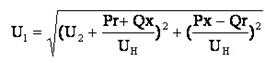
51. Дуальные цепи. Построение и свойства дуальных цепей. Правила построения.
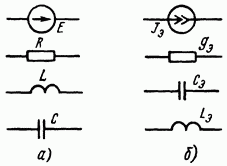
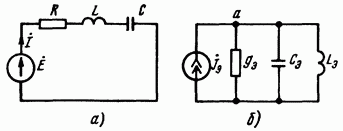 Рис.3.44. Две электрические цепи называют дуальными, если закон изменения контурных токов в одной из них подобен закону изменения узловых потенциалов в другой. В качестве простейшего примера на рис. 3.44 изображены две дуальные цепи. Схема рис. 3.44, а состоит из источника ЭДС Е и последовательно с ним включенных активного, индуктивного и емкостного элементов (R,L,C). Схема рис. 3.44, б состоит из источника тока Jэ и трех параллельных ветвей. Первая ветвь содержит активную проводимость gэ вторая — емкость Сэ третья — индуктивность Lэ. Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для схемы рис. 3.44, а уравнение по методу контурных токов:
Рис.3.44. Две электрические цепи называют дуальными, если закон изменения контурных токов в одной из них подобен закону изменения узловых потенциалов в другой. В качестве простейшего примера на рис. 3.44 изображены две дуальные цепи. Схема рис. 3.44, а состоит из источника ЭДС Е и последовательно с ним включенных активного, индуктивного и емкостного элементов (R,L,C). Схема рис. 3.44, б состоит из источника тока Jэ и трех параллельных ветвей. Первая ветвь содержит активную проводимость gэ вторая — емкость Сэ третья — индуктивность Lэ. Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для схемы рис. 3.44, а уравнение по методу контурных токов:
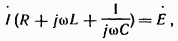 а для схемы рис. 3.44, б — по методу узловых потенциалов, обозначив потенциал точки а через
а для схемы рис. 3.44, б — по методу узловых потенциалов, обозначив потенциал точки а через 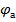 положив равным нулю потенциал второго узла:
положив равным нулю потенциал второго узла:
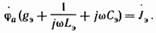 Если параметры схемы рис. 3.44, б gэ, Lэ, Сэ согласовать с параметрами схемы рис. 3,44, a R,L,C таким образом, что
Если параметры схемы рис. 3.44, б gэ, Lэ, Сэ согласовать с параметрами схемы рис. 3,44, a R,L,C таким образом, что
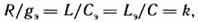 где k — некоторое произвольное число (масштабный множитель преобразования), Ом2 то
где k — некоторое произвольное число (масштабный множитель преобразования), Ом2 то
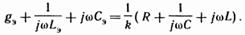
С учетом равенства (3.66) перепишем уравнение (3.64) следующим образом:
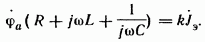 Из сопоставления уравнений (3.63) и (3.67) следует, что если ток Jэ источника тока в схеме рис. 3.44, б изменяется с той же угловой частотой, что и ЭДС Е в схеме рис. 3.44, а, и численно равен Е, а параметры обеих схем согласованы в соответствии с уравнением (3.65), то при k=1 Ом2 закон изменения во времени потенциала
Из сопоставления уравнений (3.63) и (3.67) следует, что если ток Jэ источника тока в схеме рис. 3.44, б изменяется с той же угловой частотой, что и ЭДС Е в схеме рис. 3.44, а, и численно равен Е, а параметры обеих схем согласованы в соответствии с уравнением (3.65), то при k=1 Ом2 закон изменения во времени потенциала 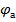 в схеме рис. 3.44, б совпадает с законом изменения во времени тока I в схеме рис. 3.44, а.
в схеме рис. 3.44, б совпадает с законом изменения во времени тока I в схеме рис. 3.44, а.
 Если свойства какой-либо из схем изучены, то они полностью могут быть перенесены на дуальную ей схему. Между входным сопротивлением Zисх исходного двухполюсника и входной проводимостью Yдуал дуального ему двухполюсника существует соотношение Zисх=k Yдуал
Если свойства какой-либо из схем изучены, то они полностью могут быть перенесены на дуальную ей схему. Между входным сопротивлением Zисх исходного двухполюсника и входной проводимостью Yдуал дуального ему двухполюсника существует соотношение Zисх=k Yдуал
Из (3.66) получаем соотношение между частотной характеристикой чисто реактивного исходного двухполюсника Хисх(ω) и частотной характеристикой дуального ему тоже чисто реактивного двухполюсника bдуал(ω).
Рис. 3.45
Действительно, так как Zисх=jXисх(ω), а Yдуал=-jbдуал(ω) т. е. частотная тарактеристика дуального двухполюсника получается из исходной частотной характеристики путем опрокидывания ее относительно оси ω и деления на масштабный множитель k.
Каждому элементу исходной схемы (схемы с источниками ЭДС Е и параметрами R, L, С) отвечает свой элемент эквивалентной дуальной схемы (схемы с источниками тока jэ и параметрами gэ, Сэ, Lэ
