Вопрос. Определение коэффициентов четырёхполюсника из опытов холостого хода и короткого замыкания
В случае, когда четырехполюсник включен между генератором и нагрузкой, то режим работы генератора будет существенно завесить от входного сопротивления четырехполюсника. В свою очередь, этот параметр будет зависеть от входного сопротивления четырехполюсника, а также сопротивления нагрузки ZН1 и ZН2. Для определения коэффициентов Zвх1 и Zвх2 выполняют опыты холостого хода и короткого замыкания, что упрощает исходную систему уравнений. Причем опыты проводятся со стороны прямого и обратного питания.
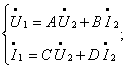
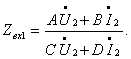
При 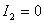 имеем:
имеем:
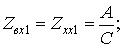
При 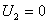 имеем:
имеем:
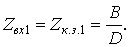
Аналогичные рассуждения могут быть получены при замене местами входа и выхода;
При 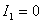 имеем:
имеем:
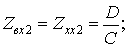
При 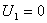 имеем:
имеем:
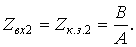
Между параметрами Zхх и Zк.з. может быть получено соотношение
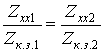 .
.
При практическом определении коэффициентов A,B,C,D через соответствующие значения сопротивления холостого хода и короткого замыкания можно воспользоваться известными методами определения комплексных входных сопротивлений. Для этого необходимо измерение напряжений, токов и мощности со стороны входных и выходных зажимов. Мощность необходимо измерять для определения угла сдвига фаз между токами и напряжениями. При этом достаточно выполнить любые три из четырех опытов для холостого хода и короткого замыкания, а затем воспользоваться уравнением связи AD – BC = 1. При работе четырехполюсника в цепи постоянного тока измерение мощности не требуется.
55. «Т» - образная схема замещения четырёхполюсника.
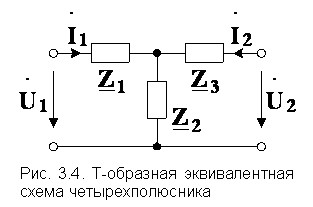 | 1. Т-образная эквивалентная схема четырехполюсника (рис. 3.4). Выразим напряжения 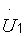 и и 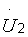 через токи через токи 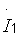 и и 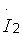 , составив уравнения по второму закону Кирхгофа. Поскольку через сопротивление , составив уравнения по второму закону Кирхгофа. Поскольку через сопротивление 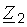 протекает ток, равный сумме токов протекает ток, равный сумме токов 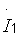 и и 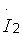 , то можно записать , то можно записать 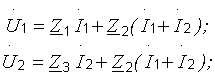 или или |
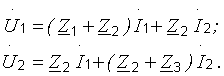 (3.7)
(3.7)
Отсюда можно получить связь между 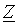 -параметрами четырехполюсника и параметрами Т-образной схемы замещения:
-параметрами четырехполюсника и параметрами Т-образной схемы замещения: 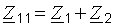 ,
, 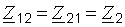 ,
, 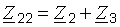 .
.
Выразив из последних двух уравнений ток 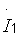 через напряжение
через напряжение 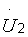 и ток
и ток 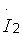 , можно определить связь между
, можно определить связь между 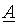 -параметрами и параметрами рассматриваемой схемы замещения. При этом необходимо учесть тот факт, что направление тока
-параметрами и параметрами рассматриваемой схемы замещения. При этом необходимо учесть тот факт, что направление тока 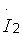 противоположно принятому за положительное ранее (см. рис. 3.3, б, 3.4). Это значит, что в системе уравнений (3.5) перед ним должен стоять знак минус. Из второго уравнения системы (3.7) имеем:
противоположно принятому за положительное ранее (см. рис. 3.3, б, 3.4). Это значит, что в системе уравнений (3.5) перед ним должен стоять знак минус. Из второго уравнения системы (3.7) имеем:
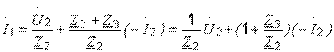 (3.8)
(3.8)
Подставив (3.8) в первое уравнение системы (3.7), получаем
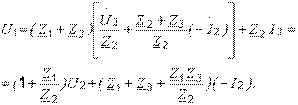 (3.9)
(3.9)
Сравнивая выражения (3.8) и (3.9) с уравнениями системы (3.5), можно установить связь между 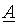 -параметрами и параметрами данной схемы замещения:
-параметрами и параметрами данной схемы замещения:
 ;
; 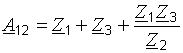 ;
;  ;
;  .
.
56. «П» - образная схема замещения четырёхполюсника.
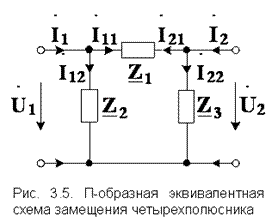 | 2. П-образная эквивалентная схема четырехполюсника (рис. 3.5). Выразим токи 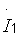 и и 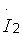 через напряжения через напряжения 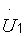 и и 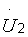 , составив уравнения по первому закону Кирхгофа: , составив уравнения по первому закону Кирхгофа: 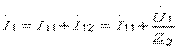 ; (3.10) ; (3.10) |
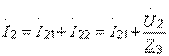 . (3.11)
. (3.11)
Поскольку 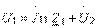 и
и 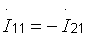 , можно записать
, можно записать

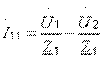 ;
; 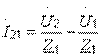 .
.
Подставляя эти выражения в (3.10) и (3.11), приходим к системе уравнений
 (3.12)
(3.12)
Сравнивая (3.12) и (3.2), можно сделать вывод, что выражения, стоящие в скобках, есть не что иное, как 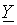 -параметры, где
-параметры, где 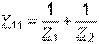 ;
; 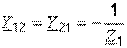 ;
;  Разрешим второе уравнение системы (3.12) относительно напряжения
Разрешим второе уравнение системы (3.12) относительно напряжения 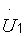 , и полученное выражение подставим в первое уравнение этой же системы. В результате получим связь параметров П-образной схемы замещения с
, и полученное выражение подставим в первое уравнение этой же системы. В результате получим связь параметров П-образной схемы замещения с 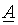 -параметрами:
-параметрами:
