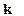Энергия взаимодействия двух электрических мульти-полей
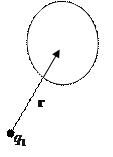
1.
Рассмотрим случай, когда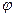 
создаётся точечным зарядом, тогда 
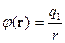, и:
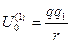-энергия взаимодействия двух точечных зарядов.
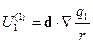
Но в силу того, что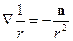 
получаем:
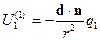-энергия взаимодействия точечного заряда и диполя
где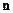 
- единичный вектор в направлении вектора 
.
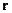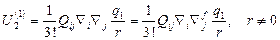
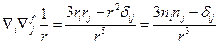
Тогда получаем:
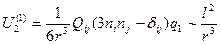
величина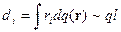 
величина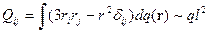 
здесь значок «~» означает «порядок»
2.
Пусть диполь создаёт поле, потенциал которого:
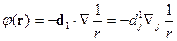
Энергия взаимодействия:
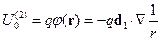- это имеет порядок такой же как и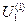 
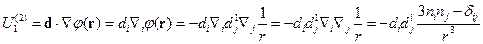
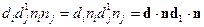
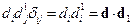
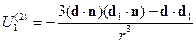-энергия взаимодействия двух диполей.
Тогда имеем формулы:
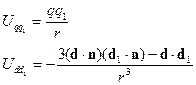
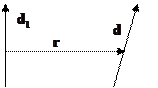
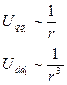
Т.е. можно ограничиться первым слагаемым при рассмотрении системы зарядов.
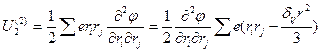
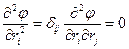
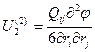
Замечание к формуле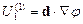 
:
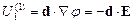
Т.е. это энергия диполя во внешнем поле (взаимодействие).
2 § 7. Дисперсионное уравнение. Нормальные электромагнитные волны в неограниченной среде
Рассматриваем нормальные волны (т.е. источников нет). Здесь свойства волны, т.е.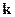 
, определяется свойствами системы, которые заключены в тензоре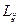 
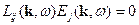
Это система однородных уравнений, решение этой системы существует, если
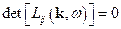(Ф7.1)
Выражение (Ф7.1) и есть дисперсионное уравнение.
Решая дисперсионное уравнение, находим допустимые значения волнового вектора 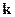и его направление.
Если в выражении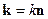 
задать направление 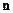, то найдём значение скорости распространения волнового вектора.
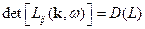
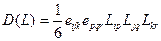
где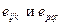 
- единичные антисимметричные тензоры.
Если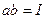 
, т.е. 
, 
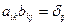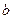- обратная к 
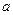матрица, тогда
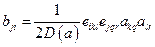(Ф7.2)
Выражение (Ф7.2) удобно для случая расчета фурье-образа тензора Грина:
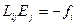
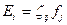
тогда
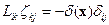
Переходим к Фурье:
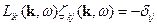
тогда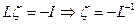 
, 
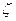считается по формуле (Ф7.2)
Условие существования нормальных электромагнитных волн – это:
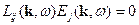
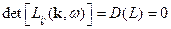
Неограниченная среда – упрощение задачи, т.к. снимаются граничные условия. Здесь на волны влияет только среда распространения волн.
3 § 8. Поперечные и продольные нормальные волны в среде. Решение дисперсионного уравнения в случае однородной и изотропной среды с пространственной дисперсией
Поперечность и продольность связываются с векторами распространения волны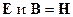 
, где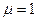 
, т.е. среда без ферромагнитных свойств.
В неограниченном пространстве для установления поперечности и продольности достаточно установить связь между векторами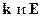 
.
|
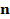, сонаправленный волновому вектору 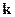. Введём единичный вектор 
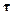, ортогональный вектору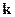 Тогда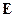 
разбивается на две составляющие:
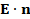- продольная составляющая
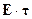- поперечная составляющая
Составляющая вектора вдоль волнового вектора 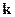поля :
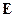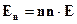
В компонентах:
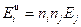
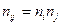- этот тензор выделяет нормальную составляющую поля .
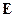Тангенциальная составляющая поля :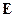
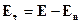
В компонентах:
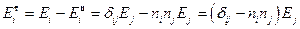
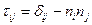-этот тензор выделяет тангенциальную (поперечную) составляющую .
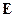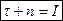- тензорное (матричное) соотношение.
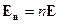
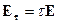
Свойство тензоров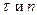 
:
это свойства операторов проектирования. В компонентах:
Решение дисперсионного уравнения приводит к поперечным или к продольным волнам. Эти решения получаются при разных условиях:
1. 
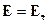при
2. 
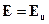при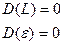 
где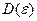 
- детерминант диэлектрических проницаемостей.
Мы будем рассматривать среды обладающие центром симметрии, т.е. проводить инверсию относительно точки – это упрощает запись тензора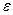 
. Тензор 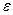может быть разложен на два независимых тензора 
:
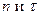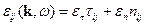
Можно показать, что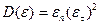 
. Тогда продольные волны могут существовать при 
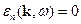. А поперечные волны могут существовать пр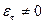и 
и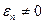 
.
Если рассчитать для 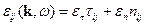выражение 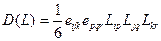, то получается уравнение Френеля:
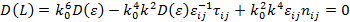
Получаем два корня данного уравнения: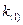 
и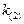 
, которые мы берём по абсолютному значению, т.е. в кристалле распространяются две поперечные волны.
В случае 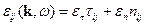решение уравнения 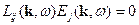может быть упрощено:
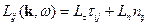
Тогда для поперечной составляющей:
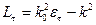
для продольной (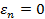 
):
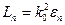
Тогда из
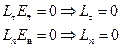
получаем
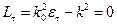
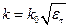(Ф8.1)
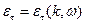
Здесь два одинаковых решения, т.к. среда изотропная.
Уравнение (Ф8.1) трансцендентное, оно решается методом последовательных приближений. В нулевом приближении можно взять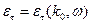 
.