Поверхностный импеданс металлов
Запишем 4-ое уравнение Максвелла без учета пространственной дисперсии:
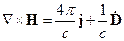
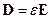
Будем рассматривать однородную и изотропную среду, т.е. 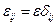 (
( 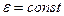 ).
).
Рассматриваем токи, возникающие в проводниках за счет поля:
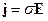 и
и 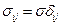 (
( 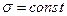 )
)
Считаем, что поля зависят от времени по закону:
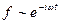
Тогда четвертое уравнение Максвелла перепишется в следующем виде:
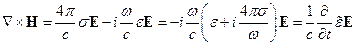
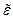 - носит комплексный характер и учитывает то, что среда проводящая. Мнимая часть
- носит комплексный характер и учитывает то, что среда проводящая. Мнимая часть 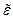 показывает ослабление поля за счет сопротивления среды:
показывает ослабление поля за счет сопротивления среды:
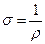 ,
, 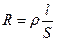
Если хороший проводник, то 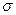 - велико.
- велико.
Ранее мы использовали условие квазистационарности 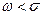 . Для идеального проводника
. Для идеального проводника 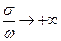 .
.
Если на проводник, обладающий параметрами 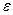 и
и 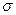 , падает электромагнитная волна, то можно ввести параметр глубины проникновения поля в проводник:
, падает электромагнитная волна, то можно ввести параметр глубины проникновения поля в проводник:
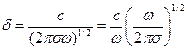
Мы знаем, что 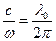 , где
, где 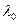 - длина волны в вакууме. Тогда
- длина волны в вакууме. Тогда 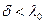 . В среде длина волны
. В среде длина волны 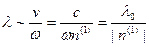
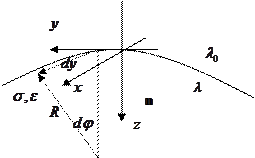
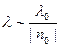
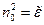 , тогда
, тогда 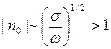
Тогда глубина проникновения поля (качественная оценка):
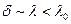
Оценим изменение поля внутри проводника.
Рассмотрим проводник, ограниченный параметром 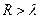 , а
, а 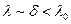 .
.
Оценим тангенциальные и нормальные производные для излучения, падающего на поверхность.
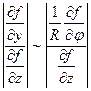
Так как излучение меняется медленно, то 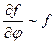 . Излучение близко к волновому, т.е.
. Излучение близко к волновому, т.е. 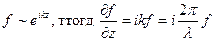 .
.
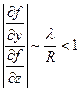 , т.е.
, т.е. 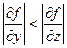
Тогда в расчетах следует учитывать слагаемые, связанные с z, а остальными можно пренебречь.
Например, 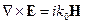 .
.
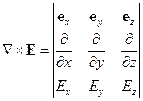
Поле Н тогда определяется тангенциальной составляющей поля Е. Если 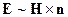 , то выбираем правовинтовую систему.
, то выбираем правовинтовую систему.
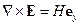
Мы получили, что связь между Е и Н носит характер волны. Более точное соотношение 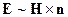 имеет вид:
имеет вид:
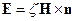 ,
,
где 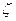 - поверхностный импеданс.
- поверхностный импеданс.
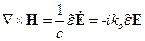
Для случая плоских волн:
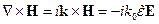
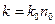 , где
, где 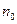 - показатель преломления.
- показатель преломления.
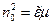 ,
, 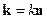
Тогда:
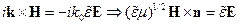 ,
,
где 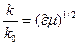 .
.
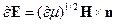 , т.е.
, т.е. 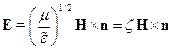
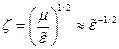
Если рассмотреть оси 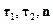 , где касательные оси
, где касательные оси 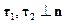 , тогда:
, тогда:
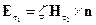
Граничное условие Леонтовича
Для расчета электромагнитного поля внутри проводника и вне проводника (вблизи него) используется граничное условие Леонтовича. Рассмотрим случай, когда точка наблюдения движется из удаленной части пространства вне проводника к поверхности проводника.
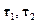 - касательные к поверхности, а
- касательные к поверхности, а 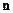 - нормаль к поверхности. Условие Леонтовича позволяет найти вещественную часть соотношения:
- нормаль к поверхности. Условие Леонтовича позволяет найти вещественную часть соотношения:
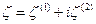
Рассмотрим вектор Пойнтинга:
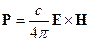
Удобно пользоваться полями Е и Н в линейных соотношениях в комплексной форме. У нас соотношение нелинейного характера, тогда надо взять реальные части полей Е и Н, тогда:
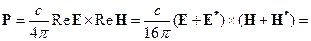
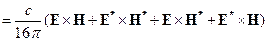
Рассмотрим случай монохроматических полей 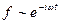 .
.
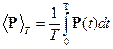 , Т – период излучения.
, Т – период излучения.
Поля излучения имеют вид:
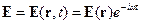 и
и 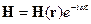
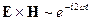 и
и 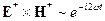
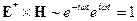 и
и 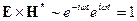
Тогда
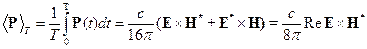
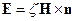
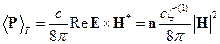
Так как величина 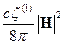 ответственна за поглощение энергии в проводнике, то
ответственна за поглощение энергии в проводнике, то