Определение расстояния между скрещивающимися прямыми

Приведем без доказательств сведения из стереометрии, необходимые для решения названной задачи.

1. Общим перпендикуляром двух скрещивающихся прямых называется отрезок,

концы которого лежат на данных прямых и который перпендикулярен к ним.

2. Общий перпендикуляр двух скрещивающихся прямых существует и единствен.

3. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

Задача. Даны скрещивающиеся прямые АВ и CD. Определить расстояние между прямыми (рис. 8.7).

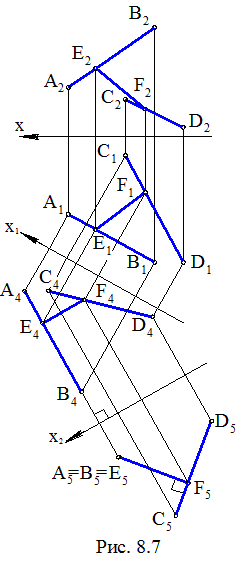Решение задачи выполним методом замены плоскостей проекций. Проекционный алгоритм решения в этом случае может быть следующим:

1) вводится новая система плоскостей проекций

П₁, П₄ , таким образом, что П₄ // АВ, т.е. на КЧ

строится ось х₁ // А₁В₁;

2) на П₄ строятся новые проекции А₄В₄ ( НВ отрезка АВ) и C₄D₄ ;

3) вводится новая система плоскостей П₄, П₅ с

осью х₂ ^ А₄В₄ такая, что П₅ ^ AB;

4) на П₅ строятся новые проекции – отрезок C₅D₅ и точка А₅ = В₅;

5) строится перпендикуляр E₅F₅ ^ C₅D₅ из точки

Е₅( = А₅ = В₅);

В итоге, по смыслу построений в методе замены плоскостей проекций и приведенному понятию расстояния между скрещивающимися прямыми, получаем, что r(E₅, C₅D₅) = r(AB, CD). Для полноты решения задачи необходимо вернуть отрезок EF длиной r(AB, CD) на исходные плоскости проекций:

1) строим E₄F₄ // x₂;

2) строим E₁F₁ по проекциям E₅F₅, E₄F₄ ; E₂F₂ по проекциям E₄F₄ , E₁F₁ .

Отрезки E₂F₂ , E₁F₁ представляют собой основные проекции отрезка EF.

В стереометрии известно еще одно определение рассматриваемого расстояния: расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведенными через эти прямые.

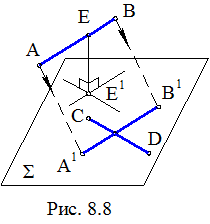Такое определение расстояния позволяет предложить более короткий путь решения рассматриваемой задачи. Пусть AB и CD – скрещивающиеся прямые (рис. 8.8). Переместим в пространстве прямую АВ параллельно самой себе в положение А¹В¹ до пересечения с CD. Если взять теперь на прямой АВ любую точку Е и опустить из этой точки перпендикуляр ЕЕ¹ на образовавшуюся плоскость Σ(CD, A¹B¹), то длина этого перпендикуляра будет искомым расстоянием r(AB,CD). Рассмотрим проекционное решение задачи.

Задача. Даны скрещивающиеся прямые АВ и CD (рис. 8.9). Определить расстояние между ними.

Решение задачи может быть следующим.

1. Перенесем прямую АВ параллельно самой себе до пересечения с CD. Таких

переносов может быть бесконечное множество. Один из переносов, например

А₁В₁ ® А₁¹В₁¹ , А₂В₂ = А₂¹В₂¹ – наиболее простой для данного КЧ вариант.

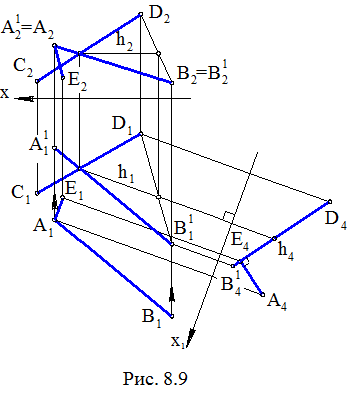2. Получаем новые условия задачи: задана плоскость Σ (А¹В¹ , CD), где А¹В¹ Ç CD и точка А; требуется определить расстояние r(А, Σ). Решение задачи выполняется методом замены плоскостей проекций по ранее изложенной схеме проекционного решения.

Определение углов

Между фигурами

Фигуры пространства: прямые линии, плоскости, прямые и плоскости могут образовывать между собой углы – геометрические фигуры с соответствующими этим фигурам величинами. Рассмотрим наиболее часто встречающиеся в начертательной геометрии углы.

Углы между прямыми

Приведем известные из школьного курса стереометрии понятия и определения, необходимые для решения последующих метрических задач:

1) плоский угол – фигура, образованная двумя лучами с общим началом и одной

из плоских областей, ограниченной ими;

2) угол между пересекающимися прямыми – величина наименьшего из плоских

углов, образованных этими прямыми;

3) угол между скрещивающимися прямыми – это угол между пересекающимися

прямыми, параллельными данным скрещивающимся прямым.

В последнем определении величина угла между двумя скрещивающимися прямыми не зависит от выбора пары пересекающихся прямых, параллельных им. Рассмотрим несколько задач на определение углов.

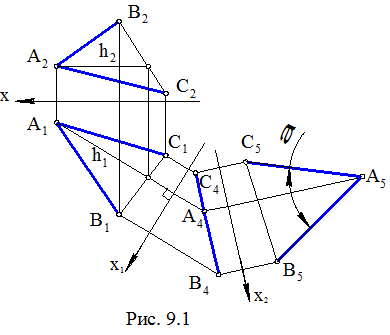
Задача.Даны пересекающиеся отрезки АВ и АС (рис. 9.1). Определить угол между ними.

Поскольку искомый угол является плоской фигурой, то решение задачи сводится к определению НВ плоской фигуры. Ее проекционное решение изложено в п. 1. Напомним алгоритм этого решения. Он основан на методе замены плоскостей проекций и применительно к условиям данной задачи может быть следующим:

1) строится линия уровня, например, h(h₁,h₂), принадлежащая плоскости Σ(АВ, АС), при этом h₂ // х;

2) строится ось проекции x₁^ h₁ , что соответствует введению в пространстве новой системы плоскостей проекций П₁, П₄, где П₄ ^ h;

3) на П₄ строится вырожденная проекция В₄С₄ плоскости Σ;

4) строится ось проекции x₂ // В₄С₄ , что соответствует введению в пространстве

новой системы плоскостей проекций П₄ , П₅ , где П₅ // Σ;

5) на П₅ строится угол Ð(А₅С₅ , А₅В₅ ) = a, который и является искомым.

Задача. Даны две скрещивающиеся прямые АВ и CD (рис. 9.2). Определить угол между ними.

Решение задачи выполним, опираясь на определение угла между скрещивающимися прямыми, приведенное выше, а также учитывая алгоритм проекционного решения предыдущей задачи. Для этих целей переместим одну из прямых, например DC, в положение, когда она, оставаясь параллельной самой себе, будет пересекать другую прямую АВ. Таких положений существует бесчисленное множество. Одно из них, например D¹C¹ (D₁¹C₁¹ , D₂¹C₂¹ ), где D₁¹С₁¹ // D₁С₁ , D₂¹С₂¹ = D₂C₂ , показано на КЧ (см. рис. 9.2). В итоге получаем пару пересекающихся прямых АВ Ç D¹С¹ , угол между которыми может быть определен на основании вышеприведенного алгоритма.

Эту часть решения задачи рекомендуется выполнить самостоятельно.

Рассмотрим еще одно проекционное решение данной задачи. Смысл его заключается в построении такой дополнительной плоскости проекций, на которой ортогональные проекции заданных скрещивающихся прямых суть пересекающиеся прямые, соответственно параллельные этим скрещивающимся прямым. Угол между такими ортогональными проекциями является искомым. Указанная плоскость проекций перпендикулярна прямой кратчайшего расстояния между заданными скрещивающимися прямыми.

Задача.Даны скрещивающиеся прямые АВ и CD. Определить угол между ними

(рис. 9.3).

Проекционное решение этой задачи, в соответствии с предложенной выше схемой, будет следующим:

1) строится ось проекции x₁ // C₁D₁ (x₁ можно строить параллельно любой из четырех ортогональных проекций прямых АВ и CD), которая вместе с плоскостями П₁ , П₄ образует новую систему плоскостей проекций, такую, что П₄ // CD;

2) на П₄ строятся дополнительные проекции А₄В₄ , C₄D₄ прямых АВ и CD, при этом C₄D₄ есть НВ отрезка CD;

3) строится ось проекции x₂ ^ C₄D₄ , которая вместе с П₄ , П₅ образует новую систему плоскостей проекций, такую, что П₅ ^CD;

4) на П₅ строятся дополнительные проекции А₅В₅ и C₅ = D₅ прямых АВ и CD;

5) строится ось проекции x₃ // А₅В₅ , которая

вместе с П₅, П₆ образует новую систему плоскостей проекций, такую, что П₆ // AB;

6) на П₆ строятся дополнительные проекции

А₆В₆ и C₆D₆ , представляющих собой НВ прямых АВ и CD и образующих между собой угол a, являющийся решением задачи.