III. Работа над новым материалом. К этому уроку для каждого ученика заготавливается из бумаги модель квадратного
К этому уроку для каждого ученика заготавливается из бумаги модель квадратного дециметра, одна сторона которой разграфлена на квадратные сантиметры.
Учитель просит детей вспомнить:
– Какую единицу измерения площади вы уже знаете? Что такое квадратный сантиметр?
Далее можно спросить:
– Удобно ли площадь стола, доски вычислять в квадратных сантиметрах?
Дети наглядно видят, что для такого измерения потребуется очень большое число квадратных сантиметров. По аналогии с единицами длины они легко догадаются, что удобнее использовать более крупные единицы измерения. Учитель помогает детям:
– Мы с вами вспомнили, что такое квадратный сантиметр, – это площадь квадрата со стороной 1 см. А не сообразите ли вы, что такое квадратный дециметр?
Найдутся учащиеся, которые скажут, что это площадь квадрата со стороной 1 дм. Учитель, подтверждая правильность такого ответа и еще раз повторяя его, показывает детям модель квадратного дециметра, а дежурные раздают учащимся подготовленные для них модели квадратного дециметра, одна из сторон которых разграфлена на квадратные сантиметры.
Учитель просит рассмотреть модель и подумать, как можно найти площадь этого квадрата в квадратных сантиметрах. Кто-то из учащихся может догадаться, что нужно 10 · 10, получится 100 см2. Учитель записывает на доске, а учащиеся в тетрадях соотношение 1 дм2= 100 см2.
После этого дети еще раз читают вводную статью в учебнике вверху.
Для закрепления под руководством учителя выполнить задания № 1, № 2, № 3.
Ф и з к у л ь т м и н у т к а
Руки в стороны – в полёт
Отправляем самолёт.
Правое крыло – вперёд,
Левое крыло – вперёд.
Раз, два, три, четыре –
Полетел наш самолёт.
(И. П. – стойка: ноги врозь, руки в стороны; 1 – поворот вправо; 2 – И. П.; 3 – поворот влево; 4 – И. П.)
IV. Работа над пройденным материалом.
Для самостоятельной работы предложить задания № 4 и № 5.
V. Итоги урока.
Учитель. Ребята, что нового мы узнали сегодня на уроке?
Дети. Мы сегодня познакомились с ещё одной новой единицей площади – квадратным дециметром и решали задачи с этой единицей площади.
Учитель. Что повторяли мы сегодня на уроке?
Дети. Решали обычные задачи и задачи на смекалку, решали также примеры.
Домашнее задание: с. 78, № 4, № 5.
У р о к 65. СОСТАВЛЕНИЕ И РАЗУЧИВАНИЕ СВОДНОЙ
ТАБЛИЦЫ УМНОЖЕНИЯ (ТАБЛИЦЫ ПИФАГОРА)(с. 79)
Цели:составить с учащимися сводную таблицу умножения и научить ею пользоваться; повторить чётные и нечётные числа; закреплять умение решать задачи изученных видов.
Ход урока
I. Организационный момент.
II. Устный счёт.
1. «Цепочка».
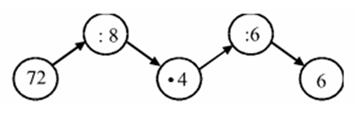
2. Даны числа 4; 5; 7; 8; 9; 12. Каждое чётное число уменьшите в 2 раза, а нечётное увеличьте в 9 раз.
Перед выполнением этого задания учащиеся должны вспомнить, какие числа называются чётными, а какие – нечётными.
3. Задание № 6. Учащиеся рассматривают рисунок, составляют задачу и отвечают на вопрос: «Во сколько раз бабочек меньше, чем стрекоз?».
III. Работа над новым материалом.
По существу новой в составляемой таблице будет только форма, поскольку со всеми случаями табличного умножения дети уже знакомы. Прежде чем вывесить печатную таблицу или обратиться к таблице, данной в начале книги на обороте ее обложки, полезно показать детям, как она составляется.
Учитель говорит: Сейчас мы составим таблицу, по которой легко найти произведение любых двух однозначных чисел от 1 до 9 (запись выполняется и на доске, и в тетрадях). Умножим теперь каждое из этих чисел на 2 и запишем полученные произведения во второй строке.
Полученное произведение надо записывать под тем числом, которое умножали.
Получается запись:
1 2 3 4 5 6 7 8 9
2 4 6 8 10 12 14 16 18
Теперь будем умножать числа верхнего ряда (подчеркнем его) на 3 и записывать полученные произведения в третьей строке, и т. д.
(Пусть дети запишут на уроке еще 2 строки из таблицы, а закончат эту работу дома.)
После этого можно вывесить плакат с таблицей Пифагора, показать, где дана эта таблица в учебнике. Сначала у доски, а потом и самостоятельно по своим таблицам дети по заданию учителя находят в таблице произведения, которые получаются при умножении на 9 (предварительно полезно спросить, в какой по счету строке будут записаны эти произведения), при умножении на 7 и т. д. Полезно предложить также найти в таблице произведения 7 · 6 и 6 · 7, произведения, получаемые при умножении одинаковых чисел, и др.
Выполняется задание № 1.
