Признаки разрешимости конечных групп
Теорема 2.2.1 (Бернсайда). Конечная бипримарная группа является разрешимой.
Теорема 2.2.2 (Фейта–Томпсона). Конечная группа нечетного порядка разрешима.
Теорема 2.2.3 (Холла). Если всякая максимальная подгруппа конечной группы  имеет своим индексом простое число или квадрат простого числа, то
имеет своим индексом простое число или квадрат простого числа, то  разрешима.
разрешима.
Теорема 2.2.4 (Виландта). Если конечная группа  содержит три разрешимые подгруппы с попарно взаимно простыми индексами, то
содержит три разрешимые подгруппы с попарно взаимно простыми индексами, то  разрешима.
разрешима.
Лемма 2.2.1. Если 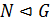 ,
, 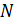 и
и 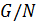 разрешимы, то
разрешимы, то  разрешима.
разрешима.
Доказательство. Пусть 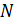 — разрешимая нормальная подгруппа группы
— разрешимая нормальная подгруппа группы  ,
, 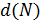 =
= 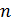 , а факторгруппа
, а факторгруппа 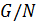 разрешима ступени разрешимости
разрешима ступени разрешимости 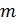 . Тогда
. Тогда
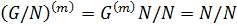
и 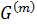 ⊆
⊆ 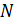 . Теперь
. Теперь
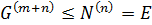
и  — разрешимая группа ступени не выше
— разрешимая группа ступени не выше 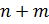 . Лемма доказана.
. Лемма доказана.
Теорема 2.2.5. Для группы  следующие утверждения эквивалентны:
следующие утверждения эквивалентны:
1.  — разрешимая группа;
— разрешимая группа;
2.Каждая неединичная подгруппа группы  отлична от своего коммутанта;
отлична от своего коммутанта;
3. Группа  обладает нормальным рядом с абелевыми факторами;
обладает нормальным рядом с абелевыми факторами;
4. Группа  обладает субнормальным рядом с абелевыми факторами.
обладает субнормальным рядом с абелевыми факторами.
Доказательство. Пусть дано утверждение 1, т.е.  — разрешимая группа. Пусть ступень разрешимости группы
— разрешимая группа. Пусть ступень разрешимости группы  равна
равна 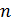 .
.
Тогда
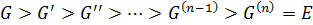 .
.
Факторы этого ряда по теореме 1.2.4 абелевы. Поэтому этот ряд является нормальным рядом с абелевыми факторами. Так как каждый нормальный ряд является субнормальным рядом, то из утверждения 1 следует утверждение 3 и 4, а из утверждения 3 следует 4.
По лемме 2.2.1 в разрешимой группе каждая подгруппа разрешима. Поэтому из утверждения 1 следует утверждение 2.
Пусть дано утверждение 4, т.е. группа  обладает субнормальным рядом
обладает субнормальным рядом
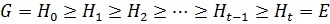
с абелевыми факторами 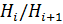 , i = 0,... ,t − 1. По теореме 1.2.4 получаем, что
, i = 0,... ,t − 1. По теореме 1.2.4 получаем, что
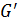 ≤
≤ 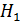 ,
, 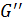 =
= 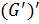 ≤
≤ 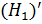 ≤
≤ 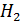 ,... ,
,... ,
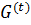 =
= 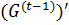 ≤
≤ 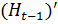 ≤
≤ 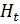 =
= 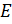
и группа  разрешима. Таким образом из утверждения 4 следует утверждение 1.
разрешима. Таким образом из утверждения 4 следует утверждение 1.
Пусть дано утверждение 2, т.е. в группе  каждая неединичная подгруппа отлична от своего коммутанта. Тогда
каждая неединичная подгруппа отлична от своего коммутанта. Тогда  >
> 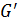 . Если
. Если 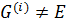 , то
, то 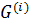 >
> 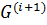 . Поэтому существует натуральное
. Поэтому существует натуральное 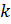 такое, что
такое, что 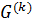 =
= 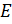 . Следовательно, группа разрешима и из утверждения 2 следует утверждение 1. Теорема доказана.
. Следовательно, группа разрешима и из утверждения 2 следует утверждение 1. Теорема доказана.
Теорема 2.2.6. Пусть  — группа порядка
— группа порядка 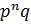 , где p и
, где p и 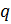 — различные простые числа. Тогда:
— различные простые числа. Тогда:
1. если 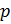 >
> 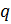 , то силовская -подгруппа нормальна в
, то силовская -подгруппа нормальна в  ;
;
2. если 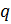 >
> 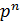 , то силовская -подгруппа нормальна в
, то силовская -подгруппа нормальна в  ;
;
3. если 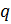 <
< 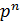 , но
, но 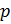 >
> 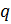 , то в группе
, то в группе  есть неединичная нормальная -подгруппа.
есть неединичная нормальная -подгруппа.
Доказательство. Пусть 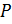 и
и 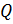 — силовские -подгруппа и
— силовские -подгруппа и 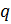 -подгруппа группы
-подгруппа группы  . Ясно, что |
. Ясно, что |  :
: 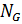 (
( 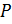 )|=1 или q, а по теореме 1.2.7
)|=1 или q, а по теореме 1.2.7
|  :
: 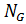 (
( 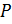 )|=1+
)|=1+ 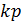 ;
; 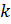 ∈
∈ 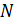 ∪{0}.
∪{0}.
Аналогично,
|  :
: 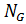 (
( 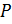 )|=
)|= 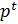 = 1+
= 1+ 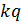 ;
; 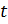 ,
, 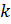 ∈
∈ 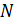 ∪{0}.
∪{0}.
1. Если 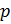 >
> 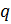 , то |
, то |  :
: 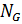 (
( 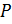 )|=1и
)|=1и 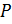 — нормальная подгруппа группы
— нормальная подгруппа группы  .
.
2. Если 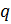 >
> 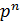 , то |
, то |  :
: 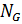 (
( 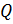 )|=1 и
)|=1 и 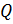 — нормальная подгруппа группы
— нормальная подгруппа группы  .
.
3. Теперь пусть 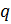 >
> 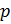 и
и 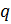 >
> 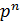 . Если
. Если 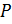 — нормальная подгруппа группы
— нормальная подгруппа группы  , то утверждение 3 справедливо. Пусть
, то утверждение 3 справедливо. Пусть 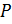 не является нормальной подгруппой группы
не является нормальной подгруппой группы  и пусть
и пусть 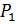 и
и 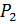 — различные силовские -подгруппы группы
— различные силовские -подгруппы группы  , для которых пересечение
, для которых пересечение 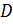 =
= 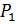 ∩
∩ 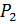 имеет наибольший порядок. Так как
имеет наибольший порядок. Так как
| 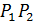 |=|
|=| 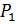 ||
|| 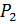 | / |
| / | 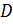 |=
|= 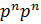 / |
/ | 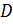 |≤
|≤ 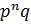 ,
,
то 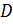
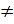
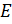 . Если
. Если 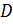 — нормальная подгруппа группы
— нормальная подгруппа группы  , то теорема доказана. Пусть
, то теорема доказана. Пусть 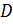 не является нормальной подгруппой группы
не является нормальной подгруппой группы  . По лемме 2.2.1 подгруппа
. По лемме 2.2.1 подгруппа 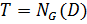 не является -группой, поэтому некоторая силовская
не является -группой, поэтому некоторая силовская 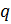 -подгруппа
-подгруппа 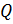 группы
группы  содержится в
содержится в 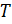 . Так как
. Так как  =
= 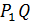 , то каждый элемент
, то каждый элемент 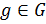 представим в виде
представим в виде 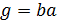 , где
, где 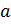 ∈
∈ 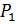 ,
, 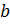 ∈
∈ 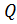 . Поэтому
. Поэтому
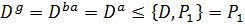 . Теорема доказана.
. Теорема доказана.
Следствие 2.2.1. Группа порядка 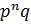 разрешима для любого
разрешима для любого 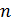 ∈
∈ 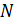 ∪{0}.
∪{0}.
Доказательство. По теореме 2.2.5 группа  порядка
порядка 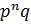 не простая и содержит неединичную примарную нормальную подгруппу
не простая и содержит неединичную примарную нормальную подгруппу 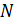 . Теперь подгруппа
. Теперь подгруппа 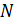 разрешима по лемме 2.1.2, а факторгруппа
разрешима по лемме 2.1.2, а факторгруппа 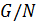 разрешима либо по индукции, либо по лемме 2.1.2. Из леммы 2.2.1 следует, что группа
разрешима либо по индукции, либо по лемме 2.1.2. Из леммы 2.2.1 следует, что группа  разрешима. Следствие доказано.
разрешима. Следствие доказано.
