Похідні та диференціали вищих порядків
Нехай функція 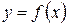 диференційовна на проміжку X, а
диференційовна на проміжку X, а 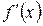 - її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної
- її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної 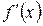 називається похідною другого порядку (second-order derivative) функції
називається похідною другого порядку (second-order derivative) функції 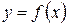 і позначається одним із символів:
і позначається одним із символів: 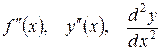
Так у фізиці, якщо 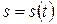 - закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то
- закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то 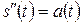 є прискоренням (acceleration) цієї точки в момент часу t. Аналогічно
є прискоренням (acceleration) цієї точки в момент часу t. Аналогічно 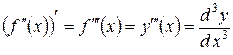 і т. д.
і т. д.
Взагалі похідною n-го порядку від функції 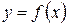 називається похідна від похідної
називається похідна від похідної 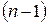 -го порядку і позначається
-го порядку і позначається 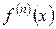 , або
, або 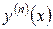 , або
, або 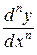
Зауваження. При 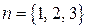 , похідну n-го порядку позначають відповідно
, похідну n-го порядку позначають відповідно 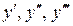 ; при
; при 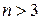 позначають:
позначають: 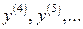 або
або 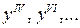 .
.
Формула Лейбніца. Якщо функції 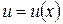 ,
, 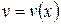 мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:
мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:
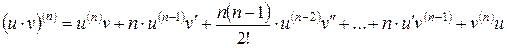 .
.
Диференціалом другого порядку (second differential)функції 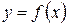 в точці x називається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім
в точці x називається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім 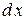 ) і позначається
) і позначається 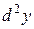 ;
; 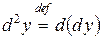
За означенням маємо 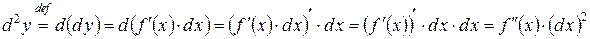
позначають 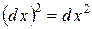 . Таким чином
. Таким чином 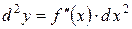 .
.
Аналогічно, диференціалом n-го порядку (позначається 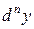 ), n=2,3,... називається диференціал від диференціала порядку
), n=2,3,... називається диференціал від диференціала порядку 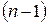 за умови, що в диференціалах весь час беруться одні й ті самі прирости
за умови, що в диференціалах весь час беруться одні й ті самі прирости 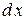 незалежної змінної x. Тобто
незалежної змінної x. Тобто 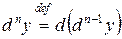 . При цьому справедлива формула:
. При цьому справедлива формула: 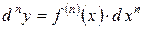
15 Теорема Ферма.
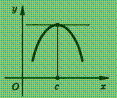
Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0. Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс
Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [а ; b] и дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).
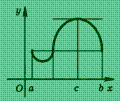
Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что 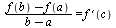 Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ.
Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х) между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ. 
Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];
2) дифференцируемы в интервале (а ; b);
3) g'(x) ≠ 0 в этом интервале,
то в интервале (а ; b) существует такая точка с, что имеет место равенство
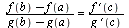
16формула Тейлора
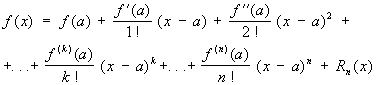
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n [то есть Rn (x) = an (x)(x—a) n, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:
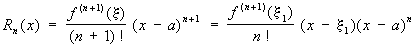
,
где ξ и ξ1 — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.
Формулой Маклоренаназывается формула Тейлора при а = 0:
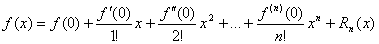
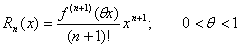
Правило Бернулі-Лопіталя
Правило говорить, що якщо функції 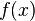 і
і 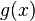 задовольняють такі умови:
задовольняють такі умови:
-
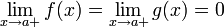 або
або 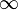 ;
; -
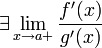 ;
; -
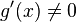 в проколотому околі
в проколотому околі 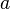 ;
; - Якщо
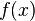 і
і 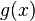 — диференційовані в проколотому околі
— диференційовані в проколотому околі 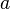 ,
,
то існує 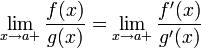 . При цьому теорема вірна і для інших баз
. При цьому теорема вірна і для інших баз
