Общий случай движения тела (для скоростей).

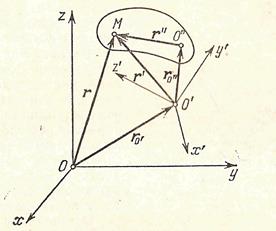" Рис 50

Рассмотрим следующую задачу в общей постановке. Твердое тело совершает произвольное движение по отношению к системе координат O'x'y'z' (рис 50), которая в свою очередь произвольным образом движется по отно­шению к неподвижной системе координат Охуz. Требуется определить абсо­лютное движение твердого тела, т.е. движение по отношению к системе ко­ординат Охуz. Движение тела по отношению к системе O'x'y'z' определим относитель­ной скоростью 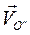его полюса О" и вектором относительной угловой ско­рости 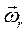вращения вокруг мгновенной оси, проходящей через полюс ОПереносное движение, т. е. движение системы O'x'y'z' по отношению к Охуz , зададим абсолютной скоростью 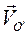полюса О' и вектором угловой скорости 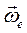вращения вокруг мгновенной оси, проходящей через О'. Определению под­лежат абсолютная скорость 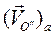полюса О" и абсолютная угловая ско­рость тела 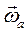. Для произвольной точки М тела, положение которой можно определить в самом теле вектор-радиусом 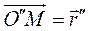, в относительной системе - вектор-радиусом 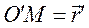и, наконец, в абсолютной системе - вектор-радиусом 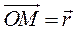, по теореме сложения скоростей имеем

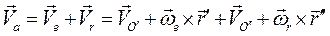(2.44)

причем два первых слагаемых дают в сумме переносную скорость 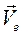точки М, а два последних - ее относительную скорость 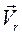. Замечая, что (рис. 50) 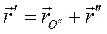будем иметь

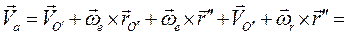
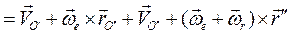Первые два слагаемых представляют собой переносную скорость полю­са О": 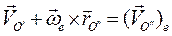, которая в сумме с относительной скоростью 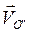того же полюса даст абсо­лютную скорость этого полюса:

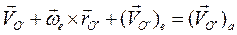
Подстановка в (2.44) дает

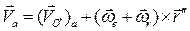
С другой стороны, согласно определению абсолютного движения ско­рость точки М может быть представлена так

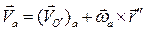
Итак, приходим к следующей тереме сложения движений твёрдого тела: распределение скоростей в абсолютном движении твёрдого тела определяется заданием абсолютной скорости полюса тела, равной геометрической сумме переносной и относительной скоростей полюса, и абсолютной угловой скорости тела, равной геометрической сумме переносной и относительной угловых скоростей тела.

Вопросы для самопроверки по кинематике.

1. Векторная формула скорости точки. Чему равна скорость точки, если ее движение задано законом

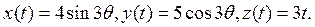
2. Векторная формула ускорения точки . Чему равно ускорение точки, если ее движение задано законом x(t)=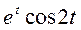

y(t)= 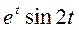z(t)= ?

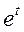3. Формула нормального ускорения точки. Когда оно равно нулю?

4. Чему равно касательное ускорение точки, если ее движение задано законом ?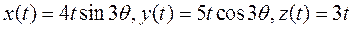

5. Как направлен вектор угловой скорости и вектор углового ускорения тела, вращающегося вокруг неподвижной оси ?

6. Какие ускорения точек тела, вращающегося вокруг неподвижной оси Вам известны?

7. Чему равно и как направлено осестремительное ускорение (скалярная и векторная форма записи)?

8. 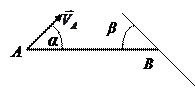Векторная формула скоростей точек плоской фигуры, постройте план скоростей.

9. Определите скорости и угловую скорость плоской фигуры, представленной на рис., если известны 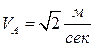, АВ=1м, α=π/4, β=π/6.

10.

Определите угловые скорости стержней АВ и ВС, если угловая скорость стержня ОА равна ω=2 (1/сек), углы ОАВ=2π/3, угол АВС- прямой ОА=АВ=ВС/2.

11. Приведите примеры нахождения мгновенного центра скоростей. Где находится мгн. центр скоростей стержня АВ в указанном примере?

12. Определить угловую скорость и угловое ускорение стержня , если АВ=l.

13. Какие углы определяют положение тела, вращающегося вокруг неподвижной точки?

14. Векторная формула скорости точек тела, вращающегося вокруг неподвижной точки.

15. Как определяется угловое ускорение тела, вращающегося вокруг неподвижной точки, прокомментируйте введенные обозначения.

16. Векторная формула сложения скоростей, чему равна переносная скорость точки?

17. Векторная формула сложения ускорений.

18. Чему равно абсолютное ускорение точки в указанном примере? Кольцо радиуса R вращается вокруг неподвижной оси с постоянной угловой скоростью ω. . По кольцу движется точка с постоянной скоростью u . Определить абсолютное ускорение точки, когда она находится в верхнем положении.

19. Чему равно ускорение Кориолиса (формула), когда оно равно нулю?

20. Чему равно и как направлено ускорение Кориолиса точки, двигающейся со скоростью 2 м/с по шатуну АВ, когда кривошип ОА вращается с угловой скоростью 1рад/с. Угол наклона кривошипа с горизонтальной плоскостью равен π/3, АВ=3 АО ?

21. Угловая скорость вращения тела относительно параллельных осей. Что такое мгновенно поступательное движение?

48. Напишите формулу Виллиса.