Указания к выполнению семестрового задания
Задания к семестровой работе
Каждое из приводимых ниже заданий предусматривает два уровня сложности. На первом уровне требуется непосредственное вычисление интегралов. Второй уровень сложности предполагает дополнительное использование ППП Mathcad. Задания этого уровня помечены символом *.
Задания и варианты индивидуальных данных
Задание 1.1) Вычислите значение I определенного интеграла от функции 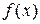 , используя метод замены переменной или интегрирования по частям. 2*) Запишите интегральные суммы
, используя метод замены переменной или интегрирования по частям. 2*) Запишите интегральные суммы 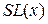 функции
функции 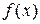 на отрезке
на отрезке 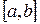 , разбивая отрезок интегрирования на
, разбивая отрезок интегрирования на 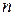 равных частей. Найдите предел
равных частей. Найдите предел 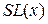 . Сравните его со значением I, найденным в п.1. 3*) Визуально отобразите проведенные исследования, постройте графики
. Сравните его со значением I, найденным в п.1. 3*) Визуально отобразите проведенные исследования, постройте графики 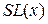 и I.
и I.
| № п/п | Интеграл | № п/п | Интеграл | № п/п | Интеграл |
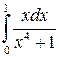 | 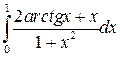 | 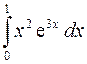 | |||
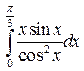 | 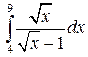 | 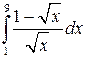 | |||
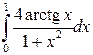 | 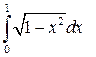 | 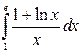 | |||
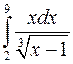 | 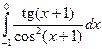 | 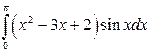 | |||
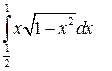 | 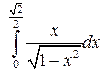 | 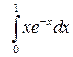 | |||
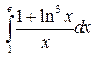 | 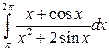 | 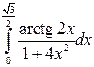 | |||
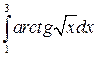 | 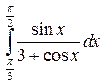 | 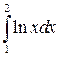 | |||
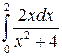 | 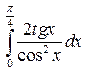 | 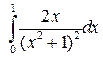 |
Задание 2.
1) Исследуйте поведение функции, заданной интегралом с переменным верхним пределом 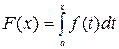 при
при 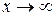 . Вычислите несобственный интеграл
. Вычислите несобственный интеграл 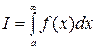 по неограниченному промежутку
по неограниченному промежутку 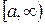 . 2*) Постройте график функции
. 2*) Постройте график функции 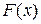 и её горизонтальной асимптоты
и её горизонтальной асимптоты 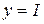 (если значение I конечно).
(если значение I конечно).
| № п/п | Интегралы | № п/п | Интегралы | № п/п | Интегралы |
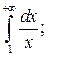 | 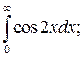 | 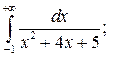 | |||
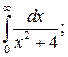 | 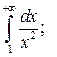 | 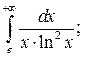 | |||
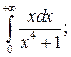 | 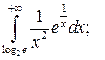 | 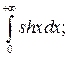 | |||
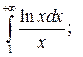 | 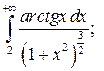 | 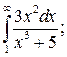 | |||
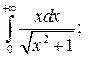 | 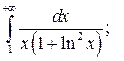 | 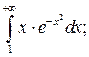 | |||
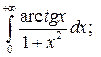 | 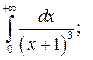 | 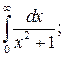 | |||
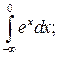 | 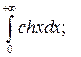 | 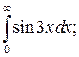 | |||
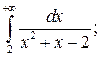 | 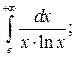 | 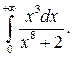 |
Задание 3. Исследуйте на сходимость 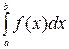 : 1) Исследуйте поведение подынтегральной функции, найдите особые точки. 2) Вычислите несобственный интеграл от неограниченной функции
: 1) Исследуйте поведение подынтегральной функции, найдите особые точки. 2) Вычислите несобственный интеграл от неограниченной функции 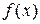 по заданному отрезку
по заданному отрезку 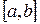 , используя его определение через предел. 3*) Постройте график функции
, используя его определение через предел. 3*) Постройте график функции 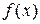 и график функции
и график функции 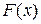 , заданной соответствующим интегралом с переменным пределом (верхним или нижним).
, заданной соответствующим интегралом с переменным пределом (верхним или нижним).
| № п/п | Интегралы | № п/п | Интегралы | № п/п | Интегралы | |
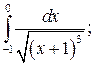 | 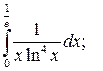 | 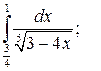 | ||||
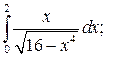 | 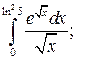 | 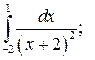 | ||||
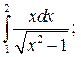 | 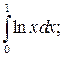 | 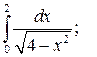 | ||||
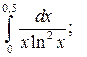 | 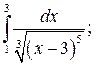 | 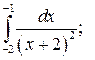 | ||||
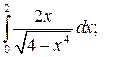 | 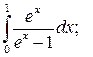 | 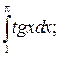 | ||||
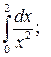 | 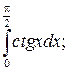 | 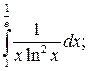 | ||||
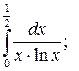 | 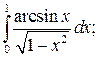 | 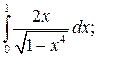 | ||||
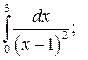 | 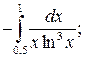 | 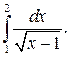 | ||||
Задание 4.1) Нарисуйте область 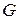 , ограниченную графиками
, ограниченную графиками 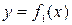 ,
, 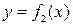 ,
, 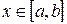 (и, быть может, прямыми
(и, быть может, прямыми 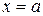 ,
, 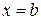 ). Вычислите её площадь. 2*) Выполните это задание в ППП Mathcad.
). Вычислите её площадь. 2*) Выполните это задание в ППП Mathcad.
| № п/п | Функции | № п/п | Функции |
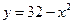 , , 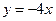 . . | 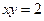 , , 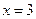 , , 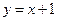 , , 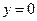 . . | ||
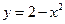 , , 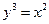 . . | 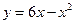 , , 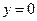 . . | ||
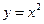 , , 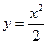 , , 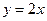 . . | 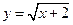 , , 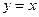 , , 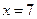 . . | ||
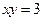 , , 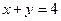 . . | 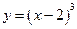 , , 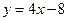 . . | ||
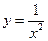 , , 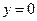 , , 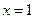 ( ( 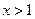 ). ). | 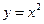 , , 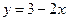 . . | ||
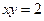 , , 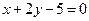 . . | 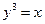 , , 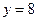 , , 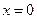 . . | ||
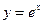 , , 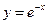 , , 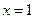 . . | 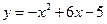 , , 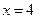 , , 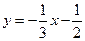 , , 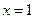 . . | ||
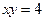 , , 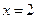 , , 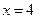 , , 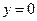 . . | 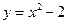 , , 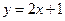 . . | ||
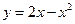 , , 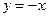 . . | 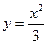 , , 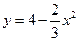 . . | ||
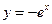 , , 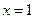 , , 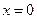 , , 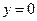 . . | 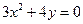 , , 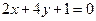 . . | ||
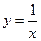 , , 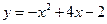 . . | 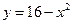 , , 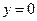 . . | ||
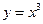 , , 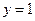 , , 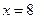 . . | 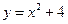 , , 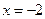 , , 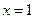 , , 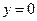 . . |
Задание 5.1) Вычислите площадь и массу 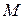 однородной пластины, ограниченной линиями, заданными уравнениями в полярной системе координат, и имеющей плотность
однородной пластины, ограниченной линиями, заданными уравнениями в полярной системе координат, и имеющей плотность 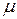 . 2*) Постройте график пластины и вычислить её площадь в ППП Mathcad.
. 2*) Постройте график пластины и вычислить её площадь в ППП Mathcad.
| № п/п | Функция | № п/п | Функция |
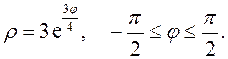 | 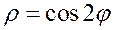 | ||
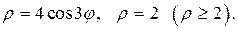 | 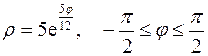 | ||
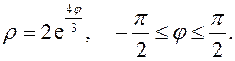 | 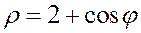 | ||
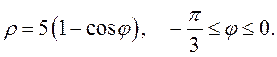 | 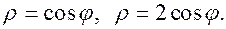 | ||
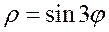 | 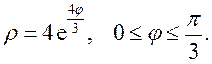 | ||
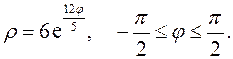 | 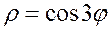 | ||
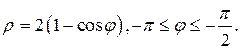 | 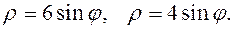 | ||
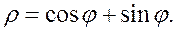 | 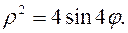 | ||
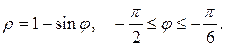 | 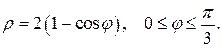 | ||
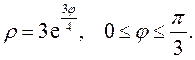 | 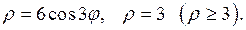 | ||
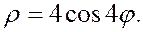 | 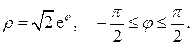 | ||
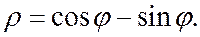 | 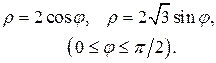 |
Задание 6.1) Вычислите длину и массу дуги однородной кривой, заданной параметрически, если её линейная плотность равна 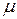 , а уравнения кривой
, а уравнения кривой 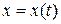 ,
, 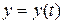 ,
, 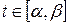 . 2*) Постройте график дуги и вычислите её длину в ППП Mathcad.
. 2*) Постройте график дуги и вычислите её длину в ППП Mathcad.
| № п/п | 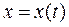 , , 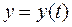 , , 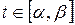 | № п/п | 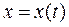 , , 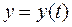 , , 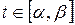 |
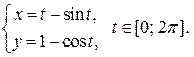 | 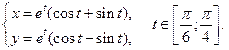 | ||
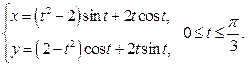 | 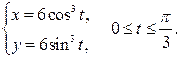 | ||
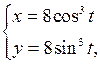 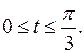 | 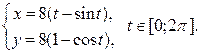 | ||
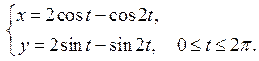 | 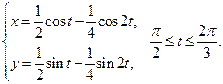 | ||
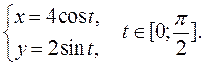 | 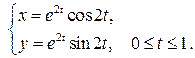 | ||
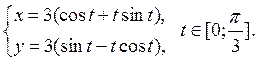 | 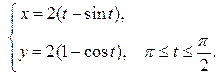 | ||
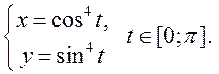 | 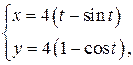 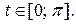 | ||
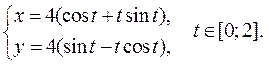 | 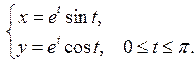 | ||
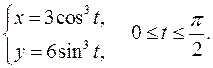 | 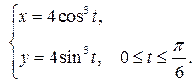 | ||
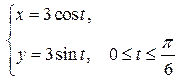 | 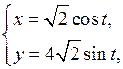 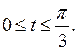 | ||
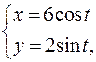 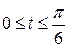 | 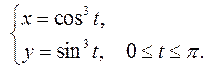 | ||
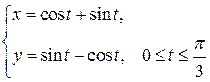 | 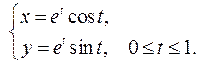 |
Задание 7.1) Вычислите объём 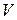 тела, образованного вращением фигуры, ограниченной графиками заданных функций, вокруг оси Ox или оси Oy. Нарисуйте схематически фигуру и полученное тело. 2*) Вычислите объём
тела, образованного вращением фигуры, ограниченной графиками заданных функций, вокруг оси Ox или оси Oy. Нарисуйте схематически фигуру и полученное тело. 2*) Вычислите объём 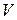 тела в ППП Mathcad.
тела в ППП Mathcad.
| № п/п | вокруг оси Ox | № п/п | вокруг оси Oy |
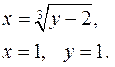 | 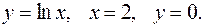 | ||
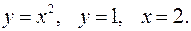 | 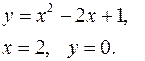 | ||
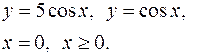 | 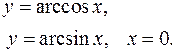 | ||
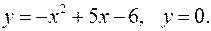 | 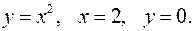 | ||
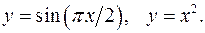 | 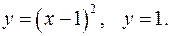 | ||
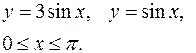 | 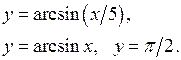 | ||
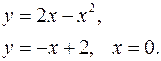 | 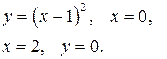 | ||
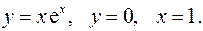 | 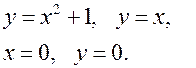 | ||
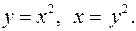 | 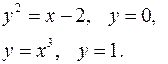 | ||
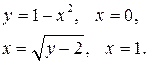 | 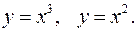 | ||
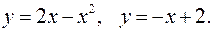 | 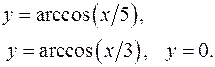 | ||
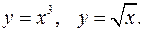 | 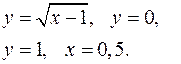 |
Указания к выполнению семестрового задания
Образцы выполнения
Задания и варианты индивидуальных данных для разных номеров вариантов приведены в п.4.1. При выполнении заданий в Mathcad предполагается, что студенты уже умеют использовать панель Calculus для ввода символов суммы, интеграла, предела, умеют строить графики в декартовой и полярной системах координат и проводить символьные вычисления, используя панель Symbolic.
Задание 1.
1) Вычислите значение I определенного интеграла от функции 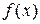 на отрезке
на отрезке 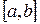 .
.
План деятельности. 1) Исходя из вида подынтегрального выражения, выберите метод решения (замена переменной или интегрирование по частям). 2) Примените соответствующую формулу. Запишите ответ.
Пример выполнения. Вычислите 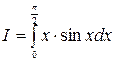 .
.
Решение. Применим формулу интегрирования по частям: 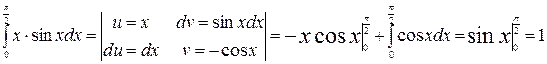 .
.
2*), 3*).
План деятельности. Разобьем отрезок 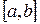 на
на 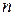 частей длины
частей длины 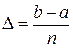 Тогда левые концы интервалов разбиения
Тогда левые концы интервалов разбиения 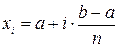 ,
, 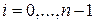 . Составим интегральную сумму
. Составим интегральную сумму 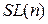 ,используя значения функции в левых концах интервалов. Вычислим её предел при
,используя значения функции в левых концах интервалов. Вычислим её предел при 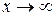 . Построим графики интегральных сумм и график
. Построим графики интегральных сумм и график 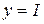 . По графику увидим, что значения интегральных сумм стремятся при
. По графику увидим, что значения интегральных сумм стремятся при 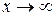 к значению определенного интеграла I.
к значению определенного интеграла I.
Образец выполнения в Mathcad:
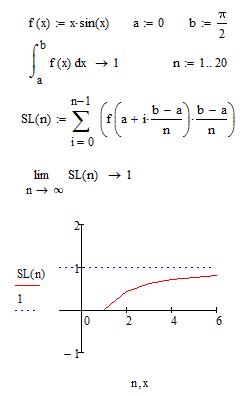 рис.4.1 рис.4.1 | а) Зададим подынтегральную функцию и пределы интегрирования. б) Вычислим символьно (используя символ n→ в панели Symbolic). в) Зададим интегральную сумму и вычислим её предел. |
Задание 2.
1) Исследуйте поведение функции, заданной интегралом с переменным верхним пределом 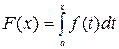 при
при 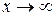 . Вычислите несобственный интеграл
. Вычислите несобственный интеграл 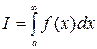 по неограниченному промежутку
по неограниченному промежутку 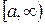 .
.
План деятельности. а) вычислите 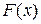 непосредственным интегрированием (или используя возможности символьного вычисления интегралов в Mathcad). б) Найдите предел
непосредственным интегрированием (или используя возможности символьного вычисления интегралов в Mathcad). б) Найдите предел 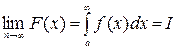 (возможно, бесконечный).
(возможно, бесконечный).
Пример выполнения. Найдем 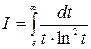 .
.
Вычислим интеграл 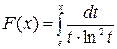 , используя метод замены переменных. Сделаем замену
, используя метод замены переменных. Сделаем замену 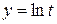 . Тогда
. Тогда 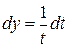 . При
. При 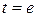
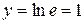 .
. 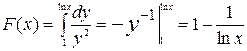 . По определению несобственного интеграла I рода
. По определению несобственного интеграла I рода 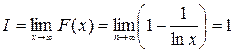 , т.е.
, т.е. 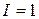 .
.
2*)
Образец выполнения в Mathcad:
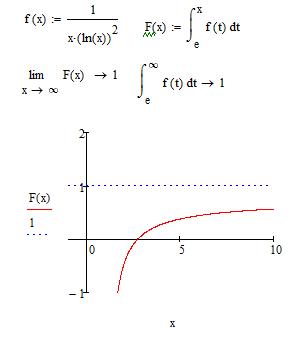 рис.4.2 рис.4.2 | а) Зададим подынтегральную функцию. б) Определим функцию 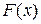 . в) Вычислим несобственный интеграл как предел функции . в) Вычислим несобственный интеграл как предел функции 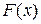 и символьно. г) Построим график функции и символьно. г) Построим график функции 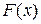 и её горизонтальной асимптоты и её горизонтальной асимптоты 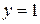 . По графику видим, как при . По графику видим, как при 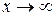 значение значение 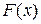 приближается к приближается к 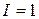 . . |
Задание 3. Исследуйте на сходимость 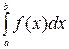 :
:
План деятельности:
1) Исследуйте поведение подынтегральной функции, найдите особые точки.
2) Вычислите несобственный интеграл от неограниченной функции 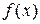 по заданному отрезку
по заданному отрезку 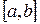 , используя его определение через предел.
, используя его определение через предел.
3*) Постройте график функции 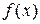 и график функции
и график функции 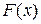 , заданной соответствующим интегралом с переменным пределом (верхним или нижним).
, заданной соответствующим интегралом с переменным пределом (верхним или нижним).
Пример выполнения. Исследовать на сходимость 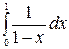 .
.
1) Подынтегральная функция 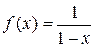 имеет в точке
имеет в точке 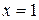 разрыв второго рода, т.к.
разрыв второго рода, т.к. 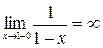 .
.
2) Рассмотрим для 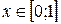
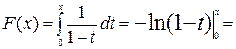
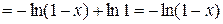 . Тогда
. Тогда 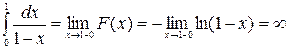 . Значит, несобственный интеграл расходится.
. Значит, несобственный интеграл расходится.
3*)
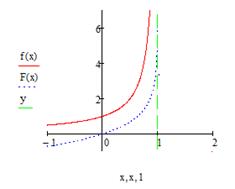 рис.4.3 рис.4.3 | На рис. 4.3 показано, что обе функции 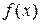 и и 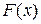 стремятся к бесконечности при стремятся к бесконечности при 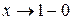 . . |
Задание 4.
1) Нарисуйте область 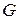 , ограниченную графиками
, ограниченную графиками 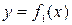 ,
, 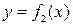 ,
, 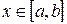 (и, быть может, прямыми
(и, быть может, прямыми 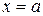 ,
, 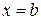 ). Вычислите её площадь.
). Вычислите её площадь.
2*) Выполните это задание в ППП Mathcad.
План деятельности.
Если область задана системой неравенств 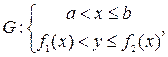 то её площадь вычисляется по формуле (3.1):
то её площадь вычисляется по формуле (3.1): 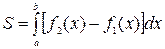 .
.
а) Если значения 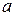 и
и 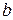 не заданы в условии, то находим их как абсциссы точек пересечения графиков функций
не заданы в условии, то находим их как абсциссы точек пересечения графиков функций 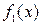 и
и 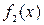 , т.е. решаем уравнение
, т.е. решаем уравнение 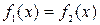 .
.
б) Исследуем, график какой из функций выше другого на 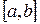 . Обозначим её через
. Обозначим её через 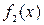 , и
, и 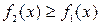 при
при 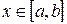 .
.
Пример выполнения. Найти площадь фигуры, ограниченной графиками функций 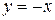 и
и 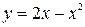 .
.
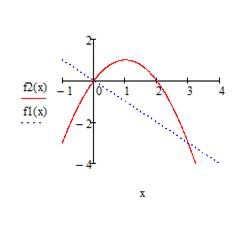 рис. 4.4 рис. 4.4 | Найдем абсциссы точек пересечения указанных графиков как корни уравнения 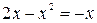 , , 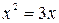 . Эти корни . Эти корни 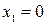 и и 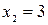 определяют пределы интегриро-вания. Т.к. на отрезке определяют пределы интегриро-вания. Т.к. на отрезке 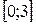 прямая прямая 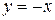 проходит ниже параболы проходит ниже параболы 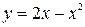 (см. рис.4.4), то (см. рис.4.4), то |
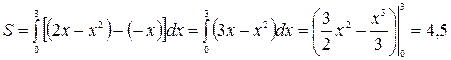 .
.
Решение примера в Mathcad:
1) Определим функции 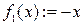 и
и 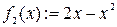 и построим их графики (рис. 4.4).
и построим их графики (рис. 4.4).
2) Найдем точки пересечения графиков, используя ключевые слова Given и Find и знак символьного равенства (< Ctrl > + < = >).
Given 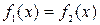
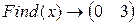
3) Определим площадь и вычислим её значение.
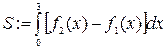
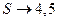 .
.
Задание 5.
1) Вычислите площадь и массу 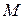 однородной пластины, ограниченной линиями, заданными уравнениями в полярной системе координат, и имеющей плотность
однородной пластины, ограниченной линиями, заданными уравнениями в полярной системе координат, и имеющей плотность 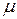 .
.
2*) Постройте график пластины и вычислите её площадь в ППП Mathcad.
Пример выполнения. Найти площадь и массу фигуры, ограниченной лемнискатой Бернулли 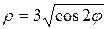 ,
, 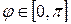 и имеющей плотность
и имеющей плотность 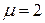 .
.
Решение. В табл. П.3 показано, что данная фигура состоит из четырех частей, симметричных относительно горизонтальной и вертикальной осей. Поэтому сначала вычислим площадь четверти данной фигуры, лежащей в первой четверти, т.е. 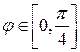 .
.
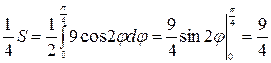 .
.
Вся площадь равна 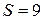 , масса
, масса 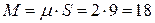 .
.
Решение примера в Mathcad:
1) Зададим 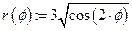
2) Для построения графика функции, заданной в полярной системе
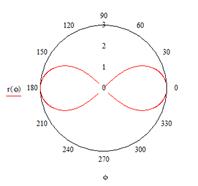 рис. 4.5 рис. 4.5 | координат, щелкните по рабочему документу, по пункту меню Graph/Polar Plot (или кнопке ). Откроется окно построения графиков.Введите в помеченные позиции имя аргумента и функции и щелкните по рабочему документу вне поля графика (рис. 4.5). |
3) Зададим площадь и вычислим её.
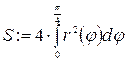
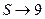 .
.
Задание 6.
1) Вычислите длину и массу дуги однородной кривой, заданной параметрически, если её линейная плотность равна 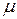 , а уравнения кривой
, а уравнения кривой 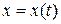 ,
, 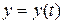 ,
, 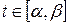 .
.
2*) Постройте график дуги и вычислите её длину в ППП Mathcad.
План деятельности.
а) Находим 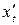 и
и 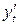 .
.
б) Вычисляем дифференциал длины дуги 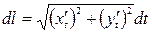 .
.
в) Длину находим как определенный интеграл: 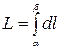 . Тогда масса
. Тогда масса 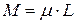 .
.
Пример выполнения. Найти длину и массу астроиды 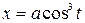 ,
, 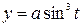 ,
, 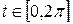 , если
, если 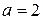 и её линейная плотность равна
и её линейная плотность равна 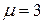 .
.
Решение. В табл. П.3 приведен график астроиды. Он получен как траектория движения точки на маленькой окружности радиуса 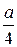 , движущейся внутри окружности, радиуса
, движущейся внутри окружности, радиуса 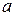 . Вычислим длину
. Вычислим длину 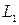 части , соответствующей значениям
части , соответствующей значениям 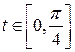 . В силу симметрии
. В силу симметрии 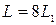 .
.
а) 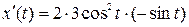 ;
; 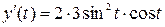 .
.
б) 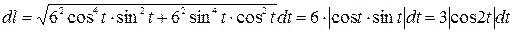 .
.
в) При 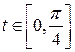
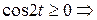
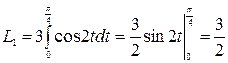 . Тогда вся длина
. Тогда вся длина 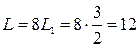 , масса
, масса 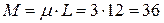 .
.
Решение примера в Mathcad:
1) График, заданный параметрически, строим, используя пункт меню X-Y Plot или соответствующую кнопку в панели инструментов Graph. В помеченных позициях возле оси Ox вводим имя аргумента, возле оси ординат - имя функции. Затем щелкните по рабочему документу вне окна графика (рис. 4.6).
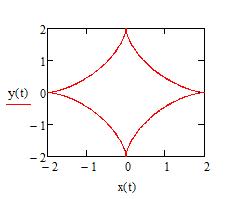 рис. 4.6 рис. 4.6 | 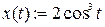 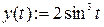 2) Определим длину формулой и вычислим её. 2) Определим длину формулой и вычислим её. 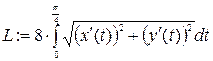 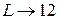 Масса и её значение Масса и её значение 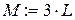 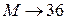 . . |
Задание 7.
1) Вычислите объём 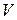 тела, образованного вращением фигуры, ограниченной графиками заданных функций, вокруг оси Ox. Нарисуйте схематически фигуру и полученное тело.
тела, образованного вращением фигуры, ограниченной графиками заданных функций, вокруг оси Ox. Нарисуйте схематически фигуру и полученное тело.
2*) Вычислите объём 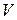 тела в ППП Mathcad.
тела в ППП Mathcad.
План деятельности.
а) если вращаемая фигура задана условиями 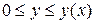 ,
, 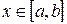 , то объём находим по формуле (3.*):
, то объём находим по формуле (3.*): 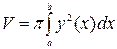 .
.
б) Если заданы только уравнения линий 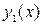 и
и 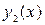 , ограничивающих фигуру, то находим точки
, ограничивающих фигуру, то находим точки 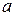 и
и 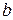 как абсциссы точек пересечения графиков этих функций, т.е. находим решения уравнений
как абсциссы точек пересечения графиков этих функций, т.е. находим решения уравнений 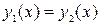 .
.
в) Исследуем знак разности 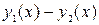 на
на 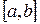 . Для этого достаточно определить знак этого выражения в какой-либо точке из
. Для этого достаточно определить знак этого выражения в какой-либо точке из 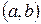 . Допустим,
. Допустим, 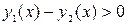 при
при 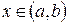 , т.е. график функции
, т.е. график функции 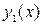 лежит выше графика
лежит выше графика 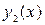 ,
, 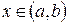 . Тогда объём вычисляется по формуле
. Тогда объём вычисляется по формуле
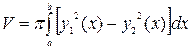 (4.*)
(4.*)
В противном случае меняем в формуле (4.*) 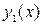 и
и 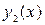 местами.
местами.
Пример выполнения. Найти объём тела, образованного вращением фигуры, ограниченной гиперболой 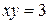 и прямыми
и прямыми 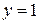 ,
, 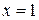 ,
, 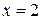 , вокруг оси Ox.
, вокруг оси Ox.
Решение. На отрезке 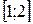 график гиперболы
график гиперболы 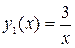 лежит выше прямой
лежит выше прямой 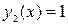 . Поэтому по формуле (4.*) вычислим
. Поэтому по формуле (4.*) вычислим
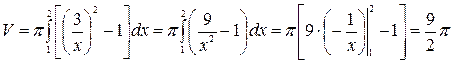 .
.
Решение примера в Mathcad:
1) Зададим верхнюю и нижнюю границы 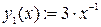 ,
, 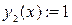 и пределы интегрирования
и пределы интегрирования 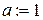 и
и 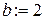 .
.
2) Определим объём формулой 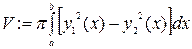 .
.
3) Вычислим объём символьно 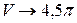 .
.
