Дослідження СЛР за методом Гаусса
Із розглянутих прикладів1–3 ми бачимо, що користуючись методом (схемою) Гаусса можна зустрітись із такими випадками:
1)СЛР зводиться до трикутної форми, провiдні елементи якої відмінні від нуля,тоді вона має єдиний розв’язок (приклад 1);
2)СЛР зводиться до трапецієподібної форми, провiдні елементи якої відмінні від нуля,тоді вона має нескінченну множину розв’язків (приклад 2);
3)В СЛР при елементарних перетвореннях з’являється співвідношення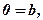 
де 
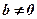. В цьому випадку СЛР розв’язків немає, вона несумісна (приклад 3).
Розв’язати систему лінійних рівнянь
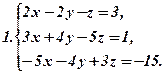
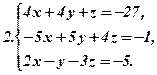
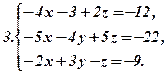
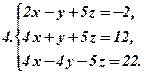
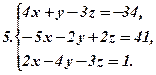
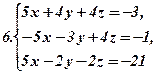
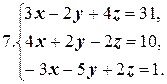
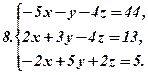
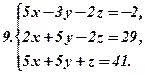
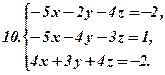
Визначники другого порядку. Системи лінійних рівнянь з двома невідомими
Поняття визначника 2-го порядку введемо, розв’язуючи систему двох рівнянь:
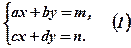
Домножимо перше з рівнянь на d, а друге - на ( - b ) і додамо їх почленно:
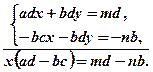
Звідки за умови, що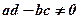 
, знаходимо х
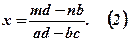
Аналогічно, виключаючи х із системи (1), знаходимо:
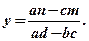(3)
Виразам в чисельниках і знаменниках для х і у можна надати більш зручної форми, якщо ввести поняття визначника.
Нехай задані числа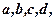 
тоді вираз 
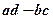називається визначником або детермінантом другого порядку і записується у вигляді:
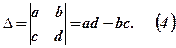
Числа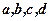 
називаються елементами визначника; 
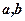- елементи першого рядка; 
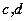- елементи другого рядка. Елементи 
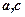і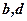 
утворюють відповідно перший і другий стовпц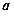і; 
і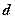 
- розміщені на головній діагоналі визначника, а про елементи 
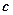і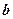 
кажуть, що вони - на побічній діагоналі.
Таким чином, визначник дорівнює добуткові елементів головної діагоналі мінус добуток елементів побічної діагоналі.
В лівій частині (4)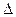 
- скорочене позначення визначника. Перехід від середньої частини рівності (4) до правої називається обчисленням визначника.
Визначники 2-го порядку мають цілий ряд властивостей, які будуть розглянуті пізніше при вивчені визначників 3-го порядку.
Тепер повернемось до системи (1).
Визначником системи (1) називається визначник, складений із коефіціентів при невідомих і позначається:
.
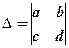Через
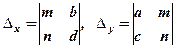
позначають допоміжні визначники, які отримуємо в першому випадку, коли коефіцієнти при х системи (1) замінимо стовпцем із вільних членів, а в другому випадку замінюються коефіцієнти при у системи (1) стовпцем із вільних членів. Тоді розв’язки (2) і (3) системи (1) можна виразити формулами
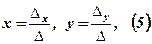
які називаються формулами Крамера[2].
Приклад. Розв’язати систему за формулами Крамера
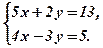
та виконати перевірку.
Розв’язання. Знайдемо визначник із коефіцієнтів системи
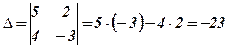
та допоміжні визначники
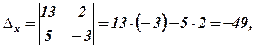
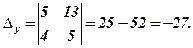
За формулами Крамера (5) знаходимо
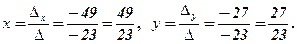
Перевірка. Підставимо знайдені значення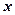 
і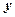 
в кожне з рівняннь
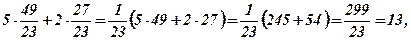
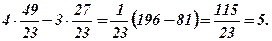
Відповідь: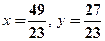 
.
Вправи
Обчислити визначники:
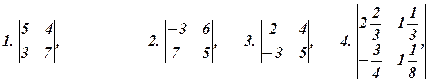
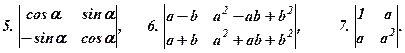
Розв’язати рівняння:
Розв’язати подані системи рівнянь та виконати перевірку:
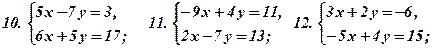
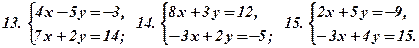
Відповіді: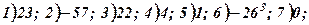 
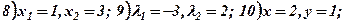
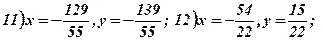
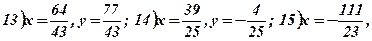
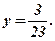
Методична порада. Якщо ваш час на розв’язання і перевірку (без допомоги калькулятора) однієї системи вигляду 10 – 15 становить більше 5 хвилин, то пропонуємо самостійно скласти і розв’язати ще декілька подібних систем (при змінних – одноцифрові коефіцієнти з різними знаками). Навики обчислення без калькулятора допоможуть вам легше і швидше вивчити наступний матеріал.
1.3. Визначники 3-го порядку. Означення. Оновні властивості
Означення: Визначником 3-го порядку називається число, отримане з дев’яти заданих чисел, розміщених у вигляді квадратної таблиці, обчислене за правилом:
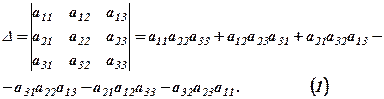Приклад. За допомогою формули (1) обчислити визначник
.
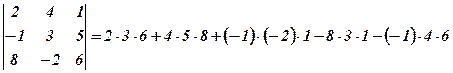
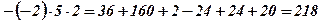Елементи визначника 3-го порядка розміщені в трьох рядках і трьох стовпцях. Якщо ввести позначення загального елемента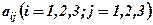 
, то перший індекс означає номер рядка, а другий з індексів - номер стовпця. Розрізняють головну (елементи 
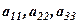) і побічну (елементи 
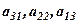) діагоналі визначника. Доданки в правій частині (1) називаються членами визначника.
Із (1) видно, що кожний член визначника містить по одному і тільки по одному елементу з кожного рядка і кожного стовпця.
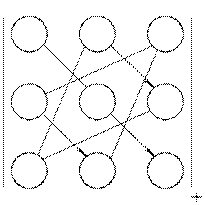
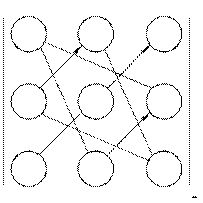
Обчислювати визначник можна за допомогою правила трикутників, яке зобразимо схематично:
  |
| — |
Члени визначника із елементів головної діагоналі, а також члени із елементів, що знаходяться у вершинах трикутників, що мають по одній стороні, паралельній головній діагоналі (ліва схема), беруться із знаком « + », а члени визначника із елементів побічної діагоналі, а також із елементів, що знаходяться у вершинах трикутників, які мають сторони, паралельні побічній діагоналі (права схема) беруться із знаком « - ».
Розглянемо основні властивості визначників 3-го порядку.
1. Величина визначника не зміниться при заміні відповідних рядків стовпцями (така заміна називається транспонуванням).
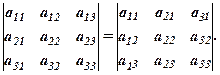
2. Знак визначника зміниться на протилежний, якщо в ньому поміняти місцями два його рядки (стовпці).
Властивості 1, 2 рекомендується перевірити самостійно згідно з формулою (1).
3. Визначник дорівнює нулю, якщо в ньому однаковими є відповідні елементи двох рядків (стовпців).
Дійсно, нехай, наприклад, у визначнику однакові елементи І-го і ІІ-го стовпців:
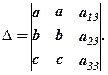
Помінявши місцями рівні стовпці, ми за властивістю 2 отримаємо новий визначник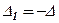 
. З іншого боку новий визначник збігається з початковим оскільки рівні відповіді елементи, тобто 
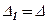. З цих рівностей маємо: 
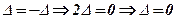. Такий же результат можна отримати безпосереднім обчисленням.
4. Визначник дорівнює нулю, якщо всі елементи одного рядка (стовпця) є нулями.
Це твердження випливає з того, що кожний член визначника за формулою (1) містить по одному і тільки по одному елементу із кожного рядка і кожного стовпця. В даному випадку по одному елементу з рядка (стовпця), що містить нулі.
5. Спільний множник елементів одного рядка (стовпця) можна винести за знак визначника.
Наприклад,
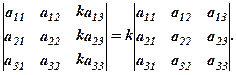
Перевірити безпосереднім обчислюванням за (1).
6. Якщо елементи одного рядка (стовпця) визначника пропорційні відповідним елементам другого рядка (стовпця), то такий визначник дорівнює нулю.
Дійсно, за властивістю 5 коефіцієнт прапорційності можна винести за знак визначника, а тоді скористатись властивістю 3.
7. Якщо кожний з елементів рядка (стовпця) визначника є сумою двох доданків, то цей визначник можна подати у вигляді суми відповідних визначників, наприклад,
Для перевірки досить записати в розгорнутому вигляді за (1) визначник, що в лівій частині рівності, тоді окремо згрупувати члени, що містять елементи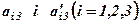 
. Кожна з отриманих груп доданків буде відповідно першим і другим визначником із правої частини рівності.
8. Значення визначника не зміниться, якщо до елемента одного рядка (стовпця) додати відповідні елементи другого рядка (стовпця), помножені на одне й теж число.
Наприклад,
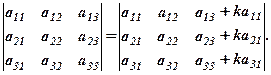
Ця рівність випливає із властивостей 6 і 7.
Приклади
1. Обчислити визначник
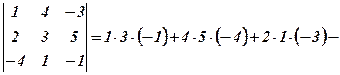
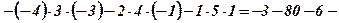
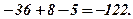
2. Перевірити першу властивість визначника
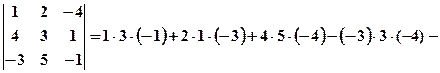
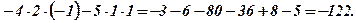
За допомогою властивостей знайти значення визначників
