Расчетные нагрузки, коэффициенты запаса

Условие прочности (1) записано через напряжения, которые вычисляются через внешние нагрузки, приложенные к конструкции. Пусть внешние нагрузки определены с точностью до одного параметра S, а напряжение s связано с этим параметром зависимостью

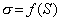
Тогда условие прочности (1) можно записать через внешние нагрузки

S < R

(3)

Здесь через R обозначено предельное значение нагрузки, т.е. такое ее значение, которое приводит к предельному состоянию

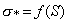
Величина R, зависящая от свойств материала и условий нагружения, называется несущей способностью или сопротивлением.

При заданном значении 5 отношение

N = R/S

называется коэффициентом запаса. Он обозначает, что сколько раз нужно увеличить нагрузку, чтобы достичь предельного состояния. Вместо условия прочности (2) можно записать эквивалентное условие

n > 1

(4)

Если нагрузка и свойства материала являются случайными, то условия прочности (3) и (4) теряют смысл, их нужно заменить вероятностными условиями типа (2):

P(S<R)=P*

или

P(n > 1)=P*

При этом коэффициент запаса n также будет случайным.

Практически расчет на прочность с учетом случайного характера внешних нагрузок и случайных свойств материала проводится следующим образом. Вводится некоторое характерное значение нагрузки [S]. Это значение, называемое допускаемым или нормативным значением, можно найти из условия

P(S<[S])=[P_S]

(5)

где [P_S] - некоторое значение вероятности, называемое обеспеченностью. Аналогично вводится нормативное значение [R] несущей способности

P(R>[R]=[P_R]

(6)

Отношение

[n]=[R]/[S]

(7)

называется нормативным коэффициентом запаса. Этот коэффициент зависит от условий нагружения, от свойств материалов, условий работы конструкции, степени ее ответственности и ряда других факторов. Такой коэффициент назначается, исходя из многолетнего опыта эксплуатации конструкций, и для каждого типа конструкций задается нормативно-технической документацией.

В качестве нормативных значений [S] и [R] можно выбрать средние значения соответствующих случайных величин

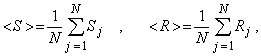
где S_j и R_j экспериментально полученные значения случайных величин в серии из N опытов. Однако в действующих нормах, в частности, строительных, нормативные значения не совпадают со средними значениями, а сдвинуты в сторону более опасных значений, что связано со значительным разбросом опытных данных около средних значений. Для нагрузки принимается несколько большее значение, а для несущей способности - меньшее

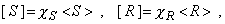
где коэффициенты c_S >1 и c_R < 1 находятся из уравнений (5) и (6). Таким образом, нормативный коэффициент запаса (7) вычисляется через средние значения следующим образом:

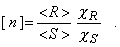
С учетом случайного характера внешних нагрузок и сопротивлений условие прочности (3) заменяется следующим условием

S_P < R_P

Здесь S_Р - достаточно редко встречающееся в реальных условиях эксплуатации высокое значение нагрузки, R_Р - также достаточно редко встречающееся низкое значение несущей способности. Эти значения называются расчетными. Они находятся из уравнений

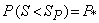
(8)

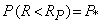
(9)

В правой части уравнений содержатся нормативные значения вероятности безотказной работы, которые близки к единице (0,95; 0,99; 0,999; ...).

Расчетные значения нагрузок и несущей способности можно выразить через средние значения этих величин следующим образом:

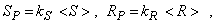
где коэффициенты k_S >1 и k_P < 1 находятся из решения уравнений (8) и (9). Расчетные значения связаны с соответствующими нормативными значениями соотношениями

S_P = k_п[S], R_P = k_o[R]

Коэффициент

k_п = k_S / c_S

называется коэффициентом однородности (меньше единицы). Другой коэффициент, учитывающий случайный характер несущей способности,

k_о = k_R / c_R

называется коэффициентом однородности (меньше единицы).

Это условие можно заменить равенством

S_P=R_P/m

где коэффициент m>1 учитывает условия работы конструкции, степень ее ответственности. С учетом обозначения (7) для нормативного коэффициента запаса получим формулу, учитывающую случайные свойства нагрузки и несущей способности, а также степень ответственности конструкции

[n] = mk_п / k_о