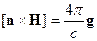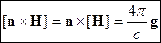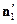Материальные уравнения или уравнения связи

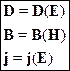
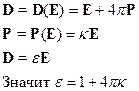
Здесь 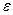- диэлектрическая проницаемость, а 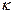- диэлектрическая восприимчивость.

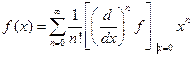-разложение функции 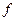в ряд Маклорена.

Если же :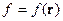

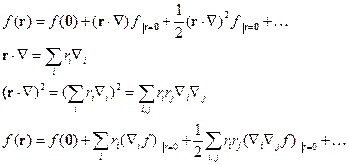
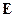Возможно разложить по векторам в ряд Маклорена:

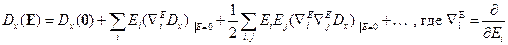
Первое слагаемое – это индукция, связанная с собственным дипольным моментом в отсутствие внешнего поля (собственная поляризация) – пироэлектричество.

Второе слагаемое – линейные среды.

Третье слагаемое – учёт нелинейности среды.

Среды, для которых нелинейные члены в разложении индукции по полю имеют вес, называются нелинейными.

Линейные среды

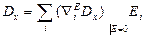
Введём обозначение: 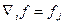, тогда

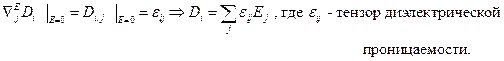
Аналогично вводятся тензоры:

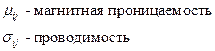
Для ферромагнетиков 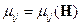- учёт нелинейности.

Неоднородные среды

Среды, для которых материальные характеристики ( 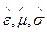) являются функциями координат.

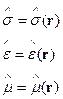
Т.е. характеристики трансляционно не инвариантны.

Введём понятие сплошной среды. Сплошная среда – это среда, в каждой точке которой измерение материальных характеристик даёт не нулевой результат. Сплошная среда – это модель. В реальной среде имеются микро-пустоты, т.е. вещество локализовано в некоторых точках пространства. Чтобы перейти к сплошной среде, нужно усреднить микропараметры по достаточно большому объёму.

Анизотропные среды

Анизотропные среды (свойства), это такие среды, свойства которых зависят от направления, в котором это свойство измеряется.

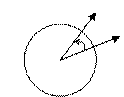Пусть в каком-то направлении исследуются оптические свойства среды. Затем мы повернули направление исследования, и оптические свойства изменились, т.е. оптические свойства зависят от угла поворота.

Так как свойства меняются, то они не инвариантны относительно вращения. Этим свойством обладает всякая анизотропная среда.

Для тензоров 2-го ранга есть исключения:

Кубические системы описываются тензорами изотропного вида, т.е.

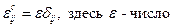
Монокристалл – есть однородная анизотропная среда.

22 § 31. Поведение электромагнитного поля при переходе через границу раздела двух сред

Рассмотрим поведение электромагнитного поля при переходе через границу раздела двух сред с различными материальными характеристиками. Используем теорему Остроградского-Гаусса и теорему Стокса:

Теорема Остроградского-Гаусса:

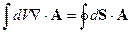
т.е. совершается следующий переход:

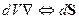
Теорема Стокса:

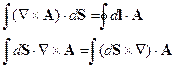
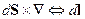
Запишем первое и четвёртое уравнения Максвелла в среде:

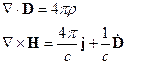
Имеется граница раздела – поверхность, отделяющая одну среду от другой.

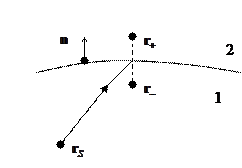
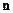- нормаль к поверхности.

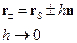
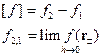
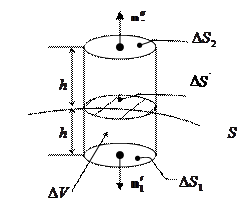
- скачок функции на границе раздела двух сред.

Рассмотрим цилиндр, образующие которого перпендикулярны поверхности 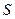. По объёму 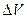проинтегрируем первое уравнение Максвелла:

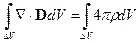
Воспользуемся теоремой Остроградского-Гаусса:

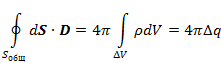
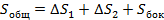
При а следовательно и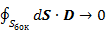

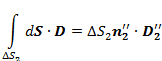
В последнем равенстве мы воспользовались теоремой о среднем.

Аналогично:

Тогда:

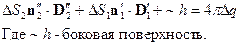
В пределе, при ,

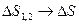
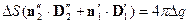
- заряд на поверхности раздела двух сред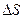

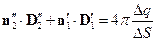
Пусть в пределе 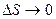, при этом

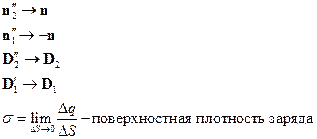
В результате получаем:

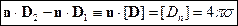
Если на поверхности нет свободных зарядов, то 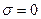и , т.е. 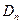- непрерывна.

Аналогично рассмотрев второе уравнение Максвелла

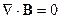
Получим

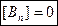
Т.е. - всегда непрерывна, её скачок всегда равен нулю.

Теперь рассмотрим четвёртое уравнение Максвелла

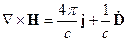
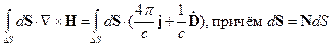Тогда по теореме Стокса:

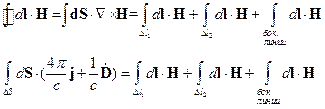
Рассмотрим левую часть этого равенства:

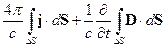
Второе слагаемое, при даёт 0.

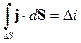- ток, протекающий через поверхность 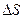, причём ток положителен в направлении нормали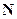

При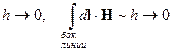

Воспользуемся теоремой о среднем:

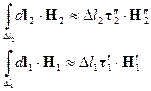
Рассмотрим предельный переход при , тогда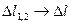

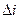- поверхностный ток, текущий через перпендикулярно чертежу.

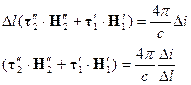
При 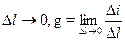- ток, текущий по поверхности, в расчёте на длину.

В результате получаем:

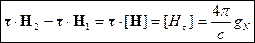
Если 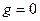, то 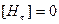- непрерывна.

Аналогично для третьего уравнения Максвелла:

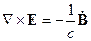
Имеем:

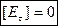
Т.е. тангенциальная составляющая электрического поля непрерывна.

Определим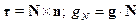

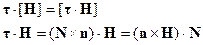
тогда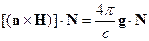

Ввиду произвольности 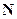, это выражение эквивалентно выражению: