Правила вычисления предела
Непрерывность функции
Определение 1. Функция 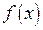 непрерывна в точке
непрерывна в точке 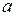 , если предел этой функции при
, если предел этой функции при 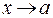 равен значению функции в предельной точке, то есть
равен значению функции в предельной точке, то есть 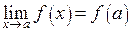 .
.
Применяя второе определение предела функции в точке, получим
Определение 2. Функция 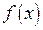 непрерывна в точке
непрерывна в точке 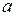 , если
, если 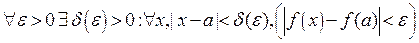 .
.
Определение 3. Функция 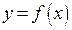 непрерывна в точке
непрерывна в точке 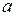 , если
, если 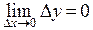 , где
, где 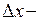 приращение аргумента функции (
приращение аргумента функции ( 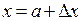 ), а
), а 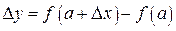 – приращение функции, соответствующее приращению ее аргумента
– приращение функции, соответствующее приращению ее аргумента 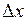 .
.
Доказательство следует из первого определения непрерывной функции
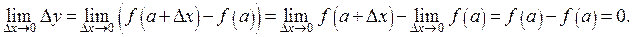 Здесь первый из пределов вычисляется с помощью определения 1, второй – как предел постоянной, поскольку
Здесь первый из пределов вычисляется с помощью определения 1, второй – как предел постоянной, поскольку 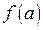 не зависит от
не зависит от 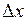 .
.
Определение 4. Функция 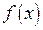 непрерывна в точке
непрерывна в точке 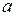 , если
, если
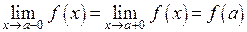 .
.
Определение 5. Функция 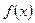 непрерывна в некоторой области, если она непрерывна во всех точках этой области.
непрерывна в некоторой области, если она непрерывна во всех точках этой области.
Все степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции непрерывны в областях существования.
Свойства непрерывных функций
Сумма непрерывных функций – есть непрерывная функция.
Действительно, из определения 1 непрерывности следует, что если 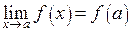 и
и 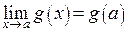 , то
, то
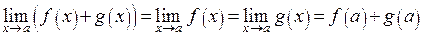 .
.
2). Произведение непрерывных функций есть функция непрерывная.
3). Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.
Доказательства второго и третьего свойств также следует из свойств пределов.
4). Пусть функция 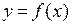 непрерывна в точке
непрерывна в точке 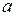 , пусть функция
, пусть функция 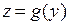 непрерывна в точке
непрерывна в точке 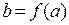 . Тогда функция
. Тогда функция 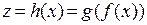 непрерывна в точке
непрерывна в точке 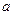 .
.
Очевидно, что 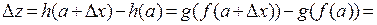
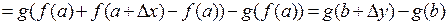 .
.
Так как согласно определению 3 непрерывности 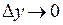 при
при 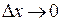 и
и 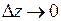 при
при 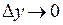 , получим:
, получим: 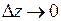 при
при 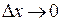 .
.
Таким образом, непрерывная функция от непрерывной функции есть функция непрерывная.
Пример. Функция 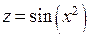 непрерывна во всех точках числовой оси, так как функция
непрерывна во всех точках числовой оси, так как функция 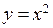 непрерывна на
непрерывна на 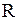 , а функция
, а функция 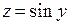 непрерывна на множестве неотрицательных чисел.
непрерывна на множестве неотрицательных чисел.
Точки разрыва функции
Определение. Точкой разрыва функции называется внутренняя точка области задания функции, в которой нарушается непрерывность функции. Если в точке разрыва функция, к тому же, не существует, ее часто называют особой точкой. Так функция 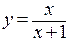 существует на всей числовой оси, кроме точки
существует на всей числовой оси, кроме точки 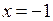 . Эта точка – особая, и в ней функция терпит разрыв.
. Эта точка – особая, и в ней функция терпит разрыв.
Разрыв может быть конечным, если 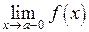 и
и 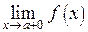 принимают конечные, но не равные значения. Разность между этими значениями называют скачком функции в точке разрыва.
принимают конечные, но не равные значения. Разность между этими значениями называют скачком функции в точке разрыва.
Пример. Функция 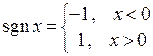 . Очевидно,
. Очевидно, 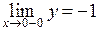 ,
,
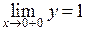 .
.
Разрыв бесконечный, если левый, правый или оба предела бесконечны.
Пример. 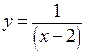 . Имеем
. Имеем 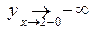 ,
, 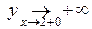 .
.
Разрыв называется устранимым, если 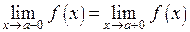 и эти пределы конечны, но функция в точке
и эти пределы конечны, но функция в точке 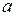 не задана.
не задана.
Пример. Функция 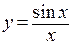 не может быть задана при
не может быть задана при 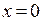 (деление на ноль), однако и левый и правый ее пределы равны 1, что следует из первого замечательного предела.
(деление на ноль), однако и левый и правый ее пределы равны 1, что следует из первого замечательного предела.
Устранить этот недостаток можно введением другой функции 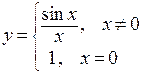 . Эта функция совпадает с заданной во всех точках, кроме 0, но она существует и непрерывна на всей числовой оси, что следует из свойств непрерывной функции.
. Эта функция совпадает с заданной во всех точках, кроме 0, но она существует и непрерывна на всей числовой оси, что следует из свойств непрерывной функции.
Вычисление пределов
Вначале выясним, в чем смысл вычисления пределов? В точках, где функция 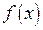 определена и непрерывна, соответствующий предел можно получить, вычислив ее значение. Особый подход к вычислению предела необходим, когда желательно знать поведение функции в окрестности особой точки, или установить, как ведет себя функция при стремлении ее аргумента к бесконечности.
определена и непрерывна, соответствующий предел можно получить, вычислив ее значение. Особый подход к вычислению предела необходим, когда желательно знать поведение функции в окрестности особой точки, или установить, как ведет себя функция при стремлении ее аргумента к бесконечности.
Рассмотрим функции 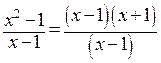 и
и 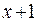 .Последняя получена в результате формального сокращения числителя и знаменателя первой на множитель
.Последняя получена в результате формального сокращения числителя и знаменателя первой на множитель 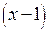 . Это разные функции, так как имеют разные области существования, хотя их значения совпадают повсюду, кроме точки
. Это разные функции, так как имеют разные области существования, хотя их значения совпадают повсюду, кроме точки 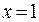 . В этой точке первая функция не существует (деление на ноль), вторая равна 2. Теперь вычислим предел
. В этой точке первая функция не существует (деление на ноль), вторая равна 2. Теперь вычислим предел 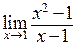 . Рассмотрим последовательность действий
. Рассмотрим последовательность действий 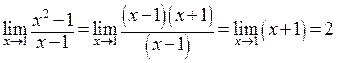 под знаком предела. Здесь мы заменяем одну функцию на другую в той области, где они совпадают, ибо при вычислении предела
под знаком предела. Здесь мы заменяем одну функцию на другую в той области, где они совпадают, ибо при вычислении предела 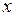 стремится к предельной точке 1, не попадая в саму эту точку. Итак, рассматриваемая функция в точке 1 не существует, но стремится к значению 2 при
стремится к предельной точке 1, не попадая в саму эту точку. Итак, рассматриваемая функция в точке 1 не существует, но стремится к значению 2 при 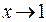 . Исследуем
. Исследуем 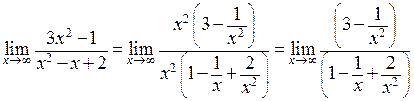 . Он равен 3, так как
. Он равен 3, так как 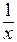 и
и 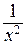 являются бесконечно малыми при
являются бесконечно малыми при 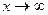 . Сокращение на
. Сокращение на 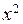 также законно, поскольку
также законно, поскольку 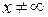 , а только стремится к бесконечности, то есть принимает сколь угодно большие, но конечные значения.
, а только стремится к бесконечности, то есть принимает сколь угодно большие, но конечные значения.
Правила вычисления предела
Чтобы вычислить 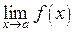 , необходимо.
, необходимо.
1. Попробовать подставить в функцию, стоящую под знаком предела, 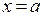 . Если функция в этой точке непрерывна, в соответствии формулой
. Если функция в этой точке непрерывна, в соответствии формулой 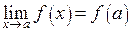 предел равен числу
предел равен числу 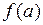 .
.
2. Если точка 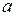 не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к
не входит в область определения функции, то конечный предел может не существовать, и если абсолютная величина функции неограниченно увеличивается при стремлении переменной к 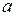 , то пределом является бесконечность.
, то пределом является бесконечность.
3. Если в результате подстановки получается неопределенность, то есть выражение вида 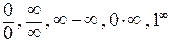 , следует раскрыть эту неопределенность, сделав сокращения, или привести получаемое выражение к замечательному пределу или его следствию. Примеры.
, следует раскрыть эту неопределенность, сделав сокращения, или привести получаемое выражение к замечательному пределу или его следствию. Примеры.
-
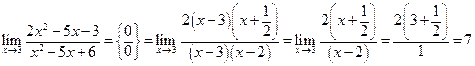 .
. -
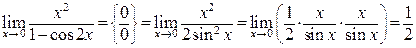 .
.
Неопределенности 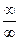 показывает, что в числителе и знаменателе присутствуют бесконечно большие функции. Чтобы избавиться от них следует вынести самую большую величину в числителе и знаменателе за скобки, произвести сокращение, после чего еще раз применить пункт 1 правил.
показывает, что в числителе и знаменателе присутствуют бесконечно большие функции. Чтобы избавиться от них следует вынести самую большую величину в числителе и знаменателе за скобки, произвести сокращение, после чего еще раз применить пункт 1 правил.
Примеры.
-
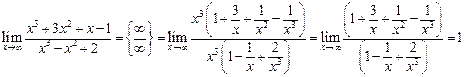 .
. -
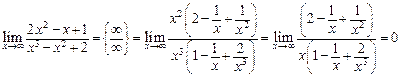 .
. - Неопределенности
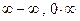 приводятся вначале к виду
приводятся вначале к виду 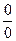 или
или 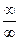 , затем раскрываются одним из перечисленных выше способов.
, затем раскрываются одним из перечисленных выше способов.
Примеры.
1) 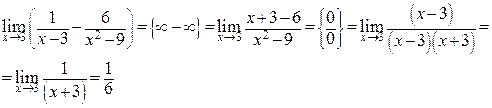
2) 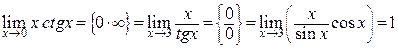 .
.
3) Проверить непрерывность функции 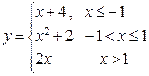 .
.
4) Поскольку функции 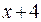 ,
, 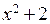 и
и 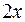 непрерывны в областях их задания, достаточно рассмотреть функцию
непрерывны в областях их задания, достаточно рассмотреть функцию 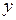 в точках стыковки этих функций. Итак, для
в точках стыковки этих функций. Итак, для 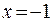 имеем
имеем 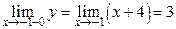 ,
, 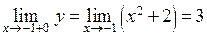 ,
, 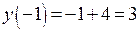 .
.
Функция в этой точке непрерывна согласно определению 4.
Для 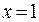 имеем
имеем 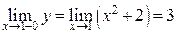 ,
, 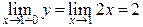 ,
, 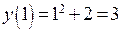 . Условие непрерывности в точке
. Условие непрерывности в точке 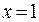 не выполняется.
не выполняется.
Следовательно, функция 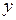 непрерывна на всей числовой оси за исключением точки
непрерывна на всей числовой оси за исключением точки 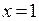 , где она имеет конечный разрыв со скачком
, где она имеет конечный разрыв со скачком
(-1).
