Обратное интерполирование для равноотстоящих узлов
Задача обратного интерполирования заключается в том, чтобы по функции  найти значение аргумента
найти значение аргумента 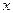 .
.
Предположим, что 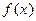 монотонна и значение
монотонна и значение  содержится между
содержится между 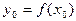 и
и 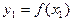 . Заменяя
. Заменяя  интерполяционным полиномом Ньютона, имеем:
интерполяционным полиномом Ньютона, имеем:
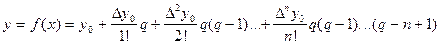
ð 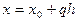 , где
, где 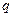 число шагов, необходимых для достижения точки
число шагов, необходимых для достижения точки 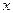 , исходя из точки
, исходя из точки 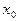 .
.
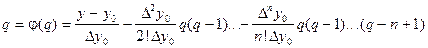
За начальное приближение принимаем:
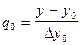
Применяя метод итерации, получим:
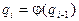
Итерационный процесс, останавливается, когда
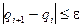 и тогда
и тогда 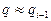 =>
=> 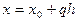
Пример:
Задано 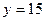 . Определить
. Определить 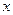 с точностью
с точностью 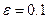
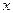 |  |
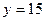
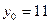
Горизонтальная таблица разностей:
| x | y | 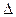 y y | 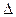 2y 2y | 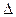 3y 3y |
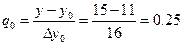

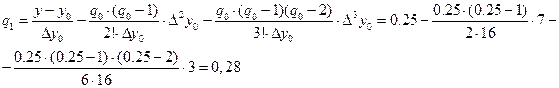
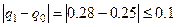 Þ
Þ 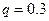
Тогда

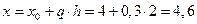
Обратное интерполирование для неравноотстоящих точек
Задача обратного интерполирования для случая неравноотстоящих точек непосредственно может быть решена с помощью интерполяционной формулы Лагранжа
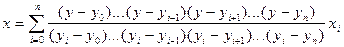
Или с помощью интерполяционной формулы Ньютона для неравноотстоящих точек
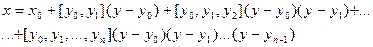
Общие выводы по задаче интерполяции
1. Для равноотстоящих узлов интерполирования лучше всего выбирать интерполяционные формулы Ньютона, при этом:
а) если значение в начале таблицы - 1ИФН
б) если значение в конце таблицы - 2ИФН
2. Существуют интерполяционные центральные формулы, позволяющие интерполировать в середине таблицы, используя близлежащие разности (Гаус, Стерлинг, Бессель)
3. Для неравноотстоящих узлов интерполирования существуют формулы Лагранжа, Ньютона.
4. Если количество узлов больше и существует возможность определения хотя бы первых производных в узлах, то лучше всего исрользовать интерполяцию сплайками.
5. Если существует возможность выбора узлов, то выбирают по условиям Чебышева, которое позволяет уменьшить погрешность аппроксимации.
6. Используя интерполяционные формулы, можно решать задачу обратного интерполирования.
7. Задача обратного интерполирования может быть использована при решении корней уравнения, а именно:
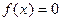 , необходимо найти корни. Составляем таблицу
, необходимо найти корни. Составляем таблицу 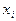
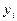 по формуле, а затем задаваясь значением
по формуле, а затем задаваясь значением 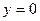 => ищат
=> ищат 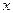 .
.
Оценка погрешности интерполяционной формулы Лагранжа
Если для функции 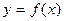 интерполяционный полином Лагранжа
интерполяционный полином Лагранжа 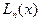 принимает в точках
принимает в точках 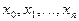 заданные значения
заданные значения 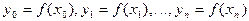 . Возникает вопрос, насколько близко построенный полином приближается к функции
. Возникает вопрос, насколько близко построенный полином приближается к функции 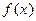 в других точках, то есть как велик остаточный член.
в других точках, то есть как велик остаточный член.
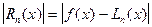
- абсолютная погрешность интерполяционной формулы Лагранжа (остаточный член)
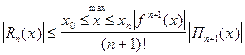
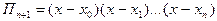
Пример: с какой точностью можно вычислить 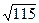 с помощью ИФЛ для функции
с помощью ИФЛ для функции 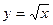
Выбрав узлы интерполирования 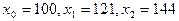
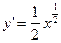 ,
, 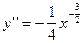 ,
, 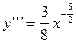
ð 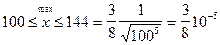
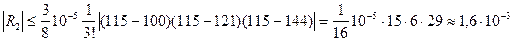
Решение системы линейных уравнений
