КОНТРОЛЬНАЯ РАБОТА № 2
Задание 1
Вариант 1
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
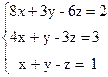
Вариант 2
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:

Вариант 3
1. Решить систему методом Гаусса, матричным методом и по формулам Крамера: 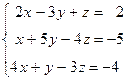
Вариант 4
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
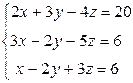
Вариант 5
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
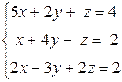
Вариант 6
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
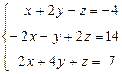
Вариант 7
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
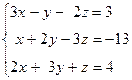
Вариант 8
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
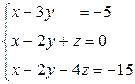
Вариант 9
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
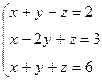
Вариант 10
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
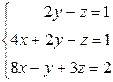
Вариант 11
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
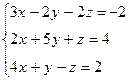
Вариант 12
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
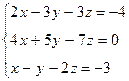
Вариант №13
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
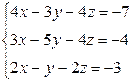
Вариант 14
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
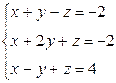
Вариант 15
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
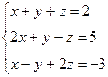
Вариант 16
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
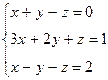
Вариант 17
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
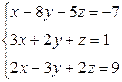
Вариант 18
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
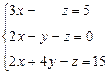
Вариант 19
1. Решить систему методом Гаусса, матричным методом и по формулам Крамера: 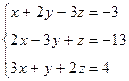
Вариант 20
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
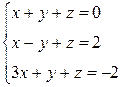
Вариант 21
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
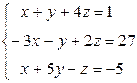
Вариант 22
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
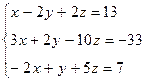
Вариант 23
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
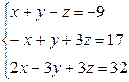
Вариант 24
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
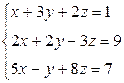
Вариант 25
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
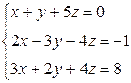
Вариант 26
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
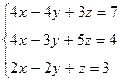
Вариант 27
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
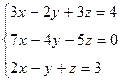
Вариант 28
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
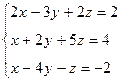
Вариант 29
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
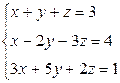
Вариант 30
- Решить систему методом Гаусса, матричным методом и по формулам Крамера:
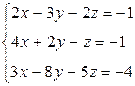
Задание 2
Вариант 1
Даны вершины А1(3,1,4), А2(-1,6,1), А3(-1,1,6 ), А4(0,4,-1 ) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5) V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 2
Даны вершины А1(3,3,9), А2(6,9,1), А3(1,7,3), А4(8,5,8 ) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7)уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 3
Даны вершины А1(3,5,4), А2(5,8,3), А3(1,9,9), А4(6,4,8) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4) S (А1А2А3 );
5) V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 4
Даны вершины А1(2,4,3), А2(7,6,3), А3(4,9,3), А4(3,6,7) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 5
Даны вершины А1(9,5,5), А2(-3,7,1), А3(5,7,8), А4(6,9,2) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 6
Даны вершины А1(0,7,1), А2(4,1,5), А3(4,6,3), А4(3,9,8) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 7
Даны вершины А1(5,5,4), А2(3,8,4), А3(3,5,10), А4(5,8,2) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 8
Даны вершины А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 9
Даны вершины А1(7,5,3), А2(9,4,4), А3(4,5,7), А4(7,9,6) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7)уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 10
Даны вершины А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 11
Даны вершины А1(3,1,4), А2(-1,6,1), А3(-1,1,6 ), А4(0,4,-1 ) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6)уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 12
Даны вершины А1(3,3,9), А2(6,9,1), А3(1,7,3), А4(8,5,8 ) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7)уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 13
Даны вершины А1(3,5,4), А2(5,8,3), А3(1,9,9), А4(6,4,8) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4) S (А1А2А3 );
5) V (А1А2А3А4 );
6) Уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 14
Даны вершины А1(2,4,3), А2(7,6,3), А3(4,9,3), А4(3,6,7) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 15
Даны вершины А1(9,5,5), А2(-3,7,1), А3(5,7,8), А4(6,9,2) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6)уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 16
Даны вершины А1(0,7,1), А2(4,1,5), А3(4,6,3), А4(3,9,8) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 17
Даны вершины А1(5,5,4), А2(3,8,4), А3(3,5,10), А4(5,8,2) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6)уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 18
Даны вершины А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6)уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 19
Даны вершины А1(7,5,3), А2(9,4,4), А3(4,5,7), А4(7,9,6) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7)уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Вариант 20
Даны вершины А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0) пирамиды.
Найти : 1) длину ребра А1А2 ;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4)S (А1А2А3 );
5)V (А1А2А3А4 );
6) уравнение высоты, опущенной из точки А4 на грань А1А2А3 ;
7) уравнение плоскости, проходящей через высоту пирамиды, опущенную из точки А4 на грань А1А2А3 и вершину А1 пирамиды.
Задание 3
Вариант 1
1. Написать уравнение плоскости, проходящей через точки 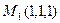 и
и 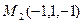 параллельно прямой, соединяющей точки
параллельно прямой, соединяющей точки 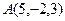 и
и 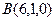 .
.
2.Показать, что прямая 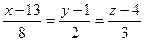 лежит в плоскости
лежит в плоскости 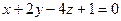 .
.
3. Даны середины сторон треугольника АВС: 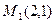 ,
, 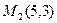 ,
, 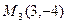 . Составить уравнения стороны ВС.
. Составить уравнения стороны ВС.
Вариант 2
1. Написать уравнение плоскости, проходящей через точку 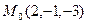 перпендикулярно линии пересечения плоскостей
перпендикулярно линии пересечения плоскостей 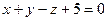 ,
, 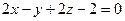 .
.
2. Составить параметрические уравнения прямой, проходящей через точки 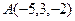 и
и 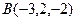 .
.
3. Дан треугольник с вершинами 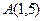 ,
, 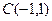 ,
, 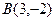 . Найти внутренний угол А этого треугольника, как угол между двумя прямыми.
. Найти внутренний угол А этого треугольника, как угол между двумя прямыми.
Вариант 3
1. Написать уравнение плоскости, проходящей через прямую 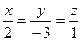 и точку
и точку 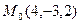 .
.
2. Составить параметрические уравнения прямой, проходящей через точку 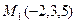 перпендикулярно плоскости
перпендикулярно плоскости 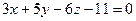 .
.
3. Написать уравнение плоскости, проходящей через точку 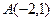 перпендикулярно прямой
перпендикулярно прямой 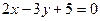 .
.
Вариант 4
1. Написать уравнение плоскости, проходящей через точку 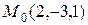 параллельно векторам
параллельно векторам 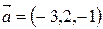 ,
, 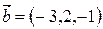 .
.
2. Даны вершины треугольника 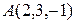 ;
; 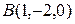 и
и 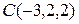 . Составить каноническое уравнение медианы АD.
. Составить каноническое уравнение медианы АD.
3. Написать уравнение прямой, проходящей через точку пересечения прямых 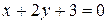 ,
, 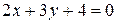 и параллельно прямой
и параллельно прямой 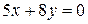 .
.
Вариант 5
1. Составить уравнение плоскости, проходящей через две точки 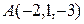 и
и 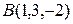 и параллельной вектору
и параллельной вектору 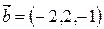 .
.
2. Доказать, что прямые параллельны 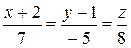
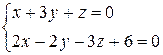 .
.
3. Даны две вершины треугольника АВС 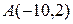 ,
, 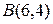 , его высоты пересекаются в точке
, его высоты пересекаются в точке 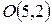 . Определить координаты третьей вершины треугольника.
. Определить координаты третьей вершины треугольника.
Вариант 6
1. Написать уравнение плоскости, проходящей через прямую 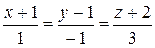 параллельно прямой
параллельно прямой 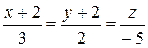
2. Найти угол между прямой 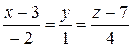 и плоскостью
и плоскостью 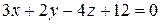 .
.
3. Даны две вершины треугольника 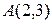 ,
, 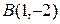 и
и 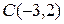 . Написать уравнение медианы АD.
. Написать уравнение медианы АD.
Вариант 7
1. Из точки 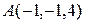 опущен на плоскость перпендикуляр; его основание
опущен на плоскость перпендикуляр; его основание 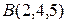 . Найти уравнение плоскости и уравнение перпендикуляра.
. Найти уравнение плоскости и уравнение перпендикуляра.
2. Написать уравнение плоскости, проходящей через пару параллельных прямых 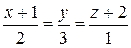 и
и 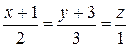 .
.
3.Найти угол между прямыми 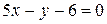 и
и 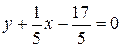 .
.
Вариант 8
1. Дана прямая 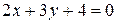 . Составить уравнение прямой, проходящей через точку
. Составить уравнение прямой, проходящей через точку 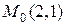 под углом в
под углом в 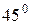 к данной прямой.
к данной прямой.
2. Написать уравнение плоскости, проходящей через данную точку 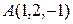 параллельно двум неколлинеарным векторам
параллельно двум неколлинеарным векторам 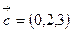 и
и 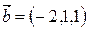 .
.
3. Составить уравнение прямой, проходящей через точку 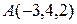 параллельно прямой:
параллельно прямой: 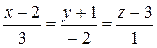 .
.
Вариант 9
1. Написать уравнение плоскости, проходящей через точку 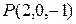 и точку
и точку 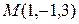 перпендикулярно к плоскости
перпендикулярно к плоскости 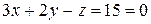 .
.
2. Найти угол между осью ОХ и прямой: 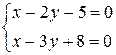 .
.
3. Даны точки 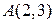 и
и 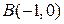 . Написать уравнение прямой, проходящей через точку В
. Написать уравнение прямой, проходящей через точку В 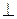 к АВ.
к АВ.
Вариант 10
1. Написать каноническое уравнение прямой, проходящей через точку 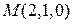 параллельно оси ОХ.
параллельно оси ОХ.
2. Найти угол между плоскостями 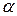 и
и 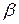 , если
, если 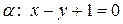 ,
, 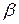 :
: 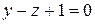 .
.
3. В равнобедренном треугольнике АВС заданы вершины 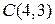 , уравнение
, уравнение 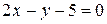 основания (АС) и уравнение
основания (АС) и уравнение 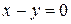 боковой стороны (АВ). Написать уравнение стороны (ВС).
боковой стороны (АВ). Написать уравнение стороны (ВС).
Вариант 11
1. Уравнение прямой 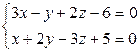 написать в каноническом и параметрическом видах.
написать в каноническом и параметрическом видах.
2. Написать уравнение прямой, проходящей через точку пересечения прямых 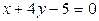 и
и 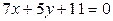 и точку А ( 5; 0).
и точку А ( 5; 0).
3. Написать уравнение плоскости, проходящей через точку А (1; -2;4 ) перпендикуляр к прямой 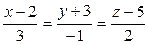 .
.
Вариант 12
1. Составить уравнение плоскости проходящей через т. М1 (2; 3;-1) и М2 (1; 0; 3) перпендикулярно плоскости 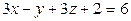
2. Написать каноническое и параметрическое уравнение прямой проходящей через т. М1 (2; -1; 1) и М2 (3; 3; -1)
3. Найти угол между прямыми: 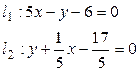
Вариант 13
1. Составить уравнение плоскости, проходящий через прямую: 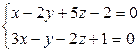 и точку М ( 2; -3; -4).
и точку М ( 2; -3; -4).
2. Написать уравнение прямой, проходящей через точку А ( 2; -3; -4) параллельно прямой: 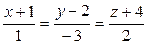 .
.
3. Найти острый угол, образованный с осью ординат прямой, проходящей через точки М ( 2; 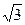 ) и N (3;
) и N (3; 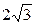 ).
).
Вариант 14
1. Составить уравнение плоскости, проходящей через две точки А ( -2; 1; -3) и В ( 1; 3; -2) и параллельной вектору 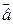 = ( -2; 2; -1).
= ( -2; 2; -1).
2. Доказать что прямые l1 и l2 параллельны 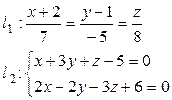
3. Даны вершины треугольника: А ( 0; 1 ), В ( 6; 5 ), С ( 12; -1 ). Написать уравнение высоты треугольника, проведённой из вершины (А). Найти величину угла (А).
Вариант 15
1. Найти уравнение плоскости, проходящей через т. М0 (2; 3; -1) параллельны векторам 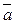 ( 3; -2; -1) и
( 3; -2; -1) и 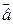 ( -1; 5; -3)
( -1; 5; -3)
2. Даны вершины треугольника А (2; 3; -1) В ( 1; -2; 0) и С (-3; 2; 2). Составить каноническое уравнение медианы (АD).
3. Написать уравнение прямой, проходящей через точку пересечения прямых 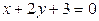 ,
, 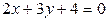 и параллельны прямой
и параллельны прямой 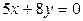 .
.
Вариант 16
1. Определить угол 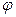 , образованный двумя прямыми:
, образованный двумя прямыми: 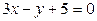 и
и 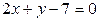 .
.
2. Составьте уравнение плоскости, которая проходит через точку А ( 2; -1; 1) перпендикулярно к двум плоскостям 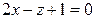 и
и 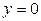 .
.
3. Найти точку пересечения прямой и плоскости: 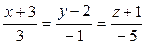 ;
; 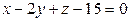 .
.
Вариант 17
1. Задана прямая линия 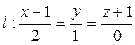 и точка М ( 0;1;2; ), М
и точка М ( 0;1;2; ), М 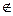 l.Написать уравнение плоскости, проходящей через эту прямую и точку М.
l.Написать уравнение плоскости, проходящей через эту прямую и точку М.
2. Написать каноническое уравнение прямой, проходящей через точку
А ( 2; 0; -1) параллельно прямой 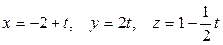 .
.
3. В треугольнике АВС координаты вершины В (2; -7). Уравнение высоты,
опущенной из вершины А: 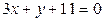 . Написать уравнение стороны ВС.
. Написать уравнение стороны ВС.
Вариант 18
1. Написать уравнение плоскости, проходящей через точки 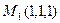 и
и 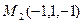 параллельно прямой, соединяющей точки
параллельно прямой, соединяющей точки 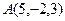 и
и 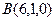 .
.
2. Показать, что прямая 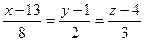 лежит в плоскости
лежит в плоскости 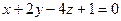 .
.
3. Даны середины сторон треугольника АВС: 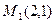 ,
, 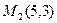 ,
, 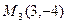 . Составить уравнения стороны ВС.
. Составить уравнения стороны ВС.
Вариант 19
1. Написать уравнение плоскости, проходящей через точку 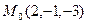 перпендикулярно линии пересечения плоскостей
перпендикулярно линии пересечения плоскостей 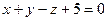 ,
, 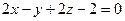 .
.
2. Составить параметрические уравнения прямой, проходящей через точки 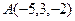 и
и 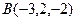 .
.
3. Дан треугольник с вершинами 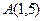 ,
, 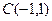 ,
, 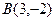 . Найти внутренний угол А этого треугольника, как угол между двумя прямыми.
. Найти внутренний угол А этого треугольника, как угол между двумя прямыми.
Вариант 20
1. Написать уравнение плоскости, проходящей через прямую 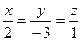 и точку
и точку 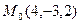 .
.
2. Составить параметрические уравнения прямой, проходящей через точку 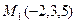 перпендикулярно плоскости
перпендикулярно плоскости 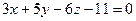 .
.
3. Написать уравнение плоскости, проходящей через точку 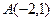 перпендикулярно прямой
перпендикулярно прямой 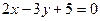 .
.
Вариант 21
1. Написать уравнение плоскости, проходящей через точку 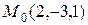
параллельно векторам 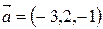 ,
, 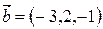 .
.
2. Даны вершины треугольника 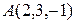 ;
; 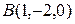 и
и 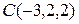 . Составить каноническое уравнение медианы АD.
. Составить каноническое уравнение медианы АD.
3. Написать уравнение прямой, проходящей через точку пересечения прямых 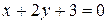 ,
, 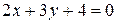 и параллельно прямой
и параллельно прямой 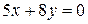 .
.
Вариант 22
1. Составить уравнение плоскости, проходящей через две точки 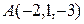 и
и 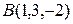 и параллельной вектору
и параллельной вектору 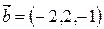 .
.
2. Доказать, что прямые параллельны 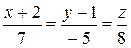
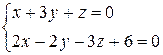 .
.
3. Даны две вершины треугольника АВС 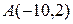 ,
, 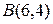 , его высоты пересекаются в точке
, его высоты пересекаются в точке 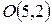 . Определить координаты третьей вершины треугольника.
. Определить координаты третьей вершины треугольника.
Вариант 23
1. Написать уравнение плоскости, проходящей через прямую 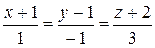 параллельно прямой
параллельно прямой 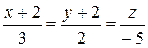
2. Найти угол между прямой 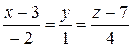 и плоскостью
и плоскостью 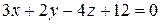 .
.
3. Даны две вершины треугольника 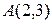 ,
, 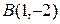 и
и 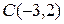 . Написать уравнение медианы АD.
. Написать уравнение медианы АD.
Вариант 24
1. Из точки 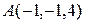 опущен на плоскость перпендикуляр; его основание
опущен на плоскость перпендикуляр; его основание 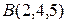 . Найти уравнение плоскости и уравнение перпендикуляра.
. Найти уравнение плоскости и уравнение перпендикуляра.
2. Написать уравнение плоскости, проходящей через пару параллельных прямых 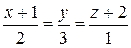 и
и 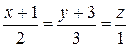 .
.
3. Найти угол между прямыми 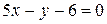 и
и 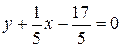 .
.
КОНТРОЛЬНАЯ РАБОТА № 2
Вычислить пределы, не применяя правило Лопиталя
Вариант 1
1. 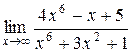 ; 2.
; 2. 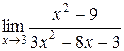 ; 3.
; 3. 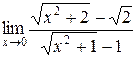 ;
;
4. 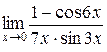 ; 5.
; 5. 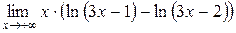 .
.
Вариант 2
1. 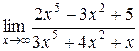 ; 2.
; 2. 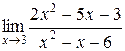 ; 3.
; 3. 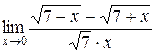 ;
;
4. 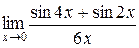 ; 5.
; 5. 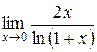 .
.
Вариант 3
1. 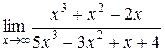 ; 2.
; 2. 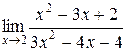 ; 3.
; 3. 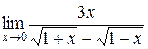 ;
;
4. 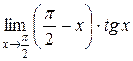 ; 5.
; 5. 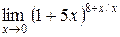 .
.
Вариант 4
1. 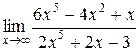 ; 2.
; 2. 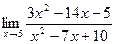 ; 3.
; 3. 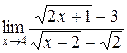 ;
;
4. 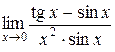 ; 5.
; 5. 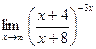 .
.
Вариант 5
1. 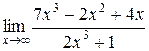 ; 2.
; 2. 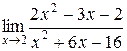 ; 3.
; 3. 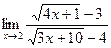 ;
;
4. 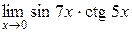 ; 5.
; 5. 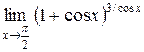 .
.
Вариант 6
1. 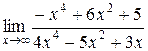 ; 2.
; 2. 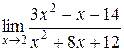 ; 3.
; 3. 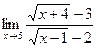 ;
;
4. 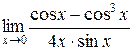 ; 5.
; 5. 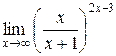 .
.
Вариант 7
1. 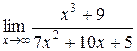 ; 2.
; 2. 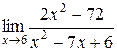 ; 3.
; 3. 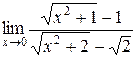 ;
;
4. 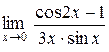 ; 5.
; 5. 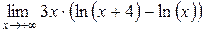 .
.
Вариант 8
1. 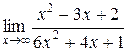 ; 2.
; 2. 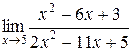 ; 3.
; 3. 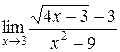 ;
;
4. 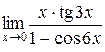 ; 5.
; 5. 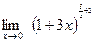 .
.
Вариант 9
1. 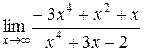 ; 2.
; 2. 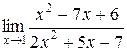 ; 3.
; 3. 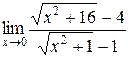 ;
;
4. 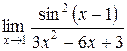 ; 5.
; 5. 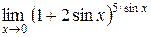 .
.
Вариант 10
