Краткие сведения из теории

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 1 (1 СЕМ.)

При решении задач (1)−(3) на вычисление производной функции одной переменной нужно использовать таблицу производных основных элементарных функций, общие правила дифференцирования, правила дифференцирования сложной функции и функции, заданной параметрическими уравнениями, а также логарифмическую производную.

Общие правила дифференцирования:

6. Правило дифференцирования сложной функции:

если .

7. При дифференцировании произведения или частного нескольких функций, а также сложно-степенной функции целесообразно использоватьлогарифмическую производную:

если то .

Этот прием называют предварительным логарифмированием.

8. Правило дифференцирования параметрически заданной функции:

если ,тоили.

При решении задачи №4 нужно написать уравнения касательной и/или нормали, проходящих через некоторую точку на заданной кривой. Эти линии являются прямыми в плоскости .

Касательную и нормаль, проходящие через точку , принадлежащую кривой, определяют три параметра: 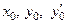. Число 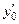равно угловому коэффициенту касательной.

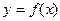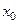à Если кривая задана явно уравнением , то . Если значение не указано, то 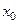надо найти из условий задачи.

à Если кривая задана параметрическими уравнениями: 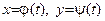, то y₀=y(t₀), x₀=j(t₀),

Если значение параметра не указано, то его надо определить, исходя из условий задачи, так как используется при вычислении 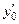и, возможно, какой-либо координаты точки .

Параметры 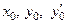удобно свести в таблицу:

Таблица 1

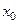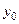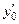Вид уравнений касательной и нормали определяется значением параметра 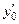. Различают три случая.

1. Если , то

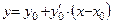− уравнение касательной,

− уравнение нормали.

2. Если , то

− уравнение касательной,

− уравнение нормали.

3. Если 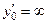, то

− уравнение касательной,

− уравнение нормали.

В первом случае и касательная, и нормаль − наклонные прямые; во втором случае касательная − горизонтальная прямая (горизонталь), нормаль − вертикальная прямая (вертикаль); в третьем случае касательная − вертикальная прямая, нормаль − горизонтальная прямая.

При решении задачи (5) на вычисление пределов функций, связанных с раскрытием неопределенностей вида , можно использовать правила Лопиталя-Бернулли: , если существует предел 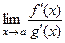. Здесь − конечная или бесконечная величина.

Ниже приведены:

− методика выполнения контрольной работы;

− типовой вариант;

− пошаговое решение типового варианта.

содержание контрольной работы

Контрольная работа №1 содержит пять заданий:

− три примера на технику дифференцирования;

− один пример на составление уравнения касательной и/или нормали к кривой;

− один пример на вычисление предела с помощью правила Лопиталя-Бернулли.

Типовой вариант КР1

Найдите производные функций:

1)

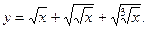
2)

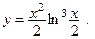
3)

4) Напишите уравнение касательной к кривой 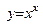в точке, где .

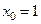5) Найдите предел