Связанные с прямой на плоскости
1. Расстояние от точки до прямой.
Пусть на евклидовой плоскости дана прямая 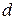 и точка
и точка 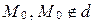 .
.
Расстоянием от точки 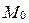 до прямой
до прямой 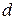 называется длина перпендикуляра
называется длина перпендикуляра 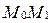 , проведенного из точки
, проведенного из точки 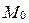 к прямой
к прямой 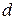 (рис. 62). Если
(рис. 62). Если 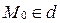 , то считают, что расстояние от
, то считают, что расстояние от 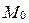 до
до 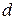 равно 0. Расстояние от точки
равно 0. Расстояние от точки 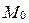 до прямой
до прямой 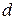 будем обозначать через
будем обозначать через 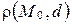 .
.
Поставим следующую задачу: вычислить 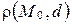 , если известны координаты точки
, если известны координаты точки 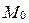 и общее уравнение прямой
и общее уравнение прямой 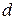 в прямоугольной декартовой системе координат. Для решения этой метрической задачи докажем теорему:
в прямоугольной декартовой системе координат. Для решения этой метрической задачи докажем теорему:
Теорема 1. Пусть в прямоугольной декартовой системе координат  даны координаты точки
даны координаты точки  и уравнение прямой
и уравнение прямой 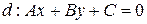 , причем
, причем 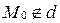 . Тогда расстояние от точки
. Тогда расстояние от точки 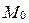 до прямой
до прямой 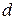 вычисляется по формуле:
вычисляется по формуле:
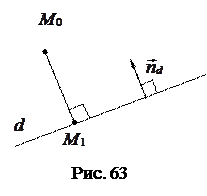
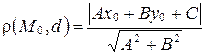 .
.
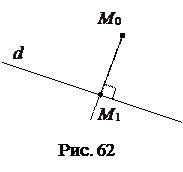 |
□ 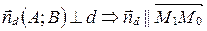 (рис. 63)
(рис. 63) 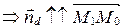 или
или 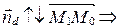
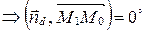 или
или 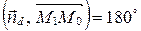 . Тогда
. Тогда
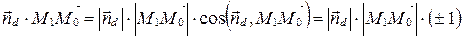 .
.
Так как 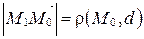 , то
, то 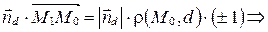
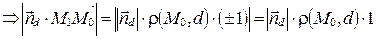 , т.к.
, т.к. 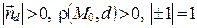 . Тогда
. Тогда 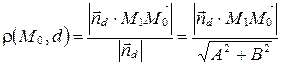 . Вычислим
. Вычислим 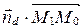 .
.
Пусть 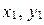 - координаты точки
- координаты точки 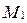 , тогда
, тогда 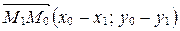 . Поэтому
. Поэтому 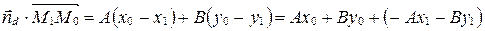 .
.
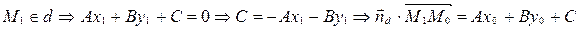 , откуда и получаем формулу
, откуда и получаем формулу
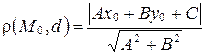 . ■
. ■
2. Направленный угол между двумя прямыми на ориентированной плоскости.
Две пересекающиеся прямые образуют на плоскости четыре угла. Углом между пересекающимися прямыми называется величина того из углов, который не превосходит остальные. Угол между прямыми 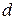 и
и  будем обозначать так:
будем обозначать так: 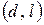 . Таким образом, для любых пересекающихся прямых
. Таким образом, для любых пересекающихся прямых 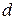 и
и 
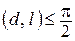 .
.
На ориентированной плоскости вводится понятие направленного (ориентированного) угла между двумя прямыми.
Пусть  - первая,
- первая,  - вторая прямая и
- вторая прямая и 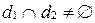 .
.
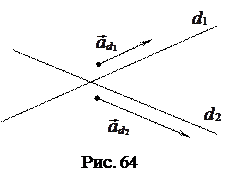 Направленным углом между прямой
Направленным углом между прямой  и прямой
и прямой  называется направленный угол между направляющими векторами
называется направленный угол между направляющими векторами 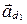 и
и 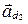 , выбранными так, что
, выбранными так, что 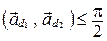 (рис. 64).
(рис. 64).
Обратите внимание, что:
– направляющие векторы прямых  и
и  берутся не произвольно, а так, что
берутся не произвольно, а так, что
величина угла между ними (обычного, не направленного) не превосходит 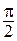 ;
;
– понятие направленного угла между прямыми определяется через понятие направленного угла между векторами.
Примем следующее обозначение направленного угла между прямой  и прямой
и прямой  :
: 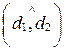 . В этой записи имеет значение порядок прямых.
. В этой записи имеет значение порядок прямых.
Из определения направленного угла между прямыми следует, что
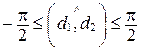 .
.
Если  не перпендикулярна
не перпендикулярна  , то
, то 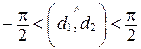 ; если
; если 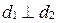 , то
, то 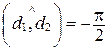 или
или 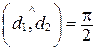 .
.
Сформулируем без доказательства следующую теорему.
Теорема 2. Если в ортонормированном базисе 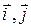 даны координаты любых направляющих векторов
даны координаты любых направляющих векторов 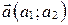 и
и 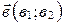 прямых
прямых  и
и  , не являющихся взаимно перпендикулярными, то
, не являющихся взаимно перпендикулярными, то
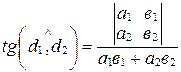 .
.
Для решения задач более важными являются два следствия из этой теоремы.
Следствие 1. Пользуясь теоремой 2, выведем формулу для вычисления 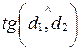 и условие перпендикулярности прямых
и условие перпендикулярности прямых  и
и  , если
, если  и
и  заданы общими уравнениями.
заданы общими уравнениями.
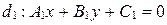 ;
; 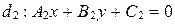 .
.
Тогда 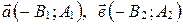 .
.
а) Если  не перпендикулярна
не перпендикулярна  , то
, то
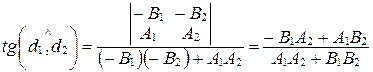 .
.
Записав числитель в виде определителя, получим
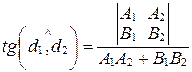 .
.
б) Если 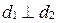 , то учитывая, что
, то учитывая, что 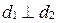 тогда и только тогда, когда
тогда и только тогда, когда 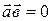 , получаем условие перпендикулярности двух прямых:
, получаем условие перпендикулярности двух прямых:
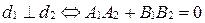 .
.
Следствие 2. Пусть прямые  и
и  заданы уравнениями с угловыми коэффициентами:
заданы уравнениями с угловыми коэффициентами: 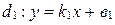 ;
; 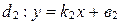 . Тогда
. Тогда 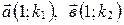 (координаты направляющих векторов
(координаты направляющих векторов 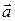 и
и 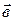 находятся после приведения уравнений прямых
находятся после приведения уравнений прямых  и
и  к общему виду).
к общему виду).
а) Если  не перпендикулярна
не перпендикулярна  , то
, то
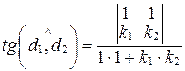 , т.е.
, т.е. 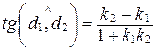 .
.
б) 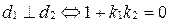 .
.
Иногда удобно пользоваться следующей записью:
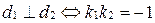 .
.
