Законы вращательного движения твердого тела

КОЛЕБАНИЯ И ВОЛНЫ. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Кинематическое уравнение гармонических колебаний материальной точки

x = A cos(wt+j),

где х - смещение; А -амплитуда колебаний; w - угловая или циклическая частота; j - начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

u = -Aw sin(wt+j); a = -Aw² cos(wt+j).

Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

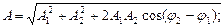
б) начальная фаза результирующего колебания

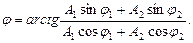
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,

x = A₁ coswt; y = A₂ cos(wt+j);

а) 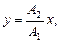если разность фаз j=0;

б) 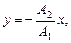если разность фаз j=±p;

в) если разность фаз j=±p/2.

Уравнение плоской бегущей волны

где y - смещение любой из точек среды с координатой x в момент t;

u - скорость распространения колебаний в среде.

Связь разности фаз Dj колебаний с расстоянием Dxмежду точками среды, отсчитанным в направлении распространения колебаний;

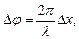
где l - длина волны.

Основное уравнение динамики вращательного движения относительно неподвижной оси z

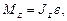
где М_z - результирующий момент внешних сил относительно оси z, действующих на тело; e - угловое ускорение; J_z - момент инерции относительно оси вращения.

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню,

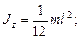
б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра),

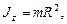
где R - радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

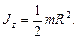
Проекция на ось z момента импульса тела, вращающегося относительно неподвижной оси z,

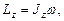
где w - угловая скорость тела.

Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси z,

= const,

где J_z - момент инерции системы тел относительно оси z; w - угловая скорость вращения тел системы вокруг оси z.

Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,

или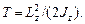

Релятивистская масса

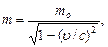или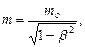

где m_o - масса покоя частицы; u - ее скорость; с - скорость света в вакууме; b - скорость частицы, выраженная в долях скорости света

(b = u/с).

Взаимосвязь массы и энергии релятивистской частицы

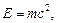или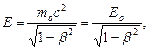

где Е_о=m_ос² - энергия покоя частицы.

Полная энергия свободной частицы

Е = Е_о + Т,

где Т - кинетическая энергия релятивистской частицы.

Кинетическая энергия релятивистской частицы

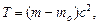или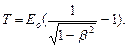

Импульс релятивистской частицы

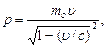или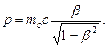

Связь между полной энергией и импульсом релятивистской частицы

Примеры решения задач

Пример 1. Платформа в виде сплошного диска радиусом R=1,5 м и массой m₁=180 кг вращается около вертикальной оси с частотой n=10 мин^-1. В центре платформы стоит человек массой m₂=60 кг. Какую линейную скорость u относительно пола помещения будет иметь человек, если он перейдет на край платформы?

Решение. Согласно условию задачи, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, можно считать равным нулю. При этом условии проекция L_z момента импульса системы платформа-человек остается постоянной:

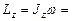const, (1)

где J_z - момент инерции платформы с человеком относительно оси z;

w - угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому в начальном состоянии а в конечном состоянии .

С учетом этого равенство (1) примет вид

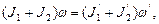(2)

где значения моментов инерции J₁ и J₂ платформы и человека соответственно относятся к начальному состоянию системы; 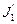и 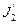- к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: 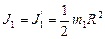. Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном состоянии (в центре платформы)можно считать равным нулю. В конечном состоянии (на краю платформы) момент инерции человека

Подставим в формулу (2) выражения моментов инерции, начальной угловой скорости вращения платформы с человеком (w = 2pn) и конечной угловой скорости (w^' = u/R, где u - скорость человека относительно пола):

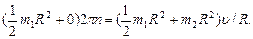
После сокращения на R² и простых преобразований находим скорость

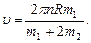
Произведем вычисления:

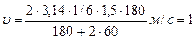м/с.

Пример 2. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение силы F_max, действующей на частицу.

Решение. Для определения амплитуды колебаний воспользуемся выражением полной энергии частицы:

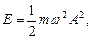
где w = 2p/Т. Отсюда амплитуда

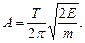(1)

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой и, следовательно, может быть выражена соотношением F = -kx, где k - коэффициент квазиупругой силы; х - смещение колеблющейся точки. Максимальной сила будет при максимальном смещении x_max, равном амплитуде:

F_max = kA. (2)

Коэффициент k выразим через период колебаний:

k = mw² = m×4p²/T². (3)

Подставив выражения (1) и (3) и (2) и произведя упрощения, получим

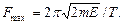
Произведем вычисления:

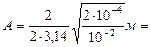0,045 м = 45 мм;

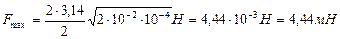
Пример 3.Складываются два колебания одинакового направления, выраженные уравнениями

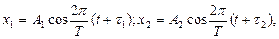
где А₁ = 3 см, А₂ = 2 см, t₁ = 1/6 с, t₂ = 1/3 с, Т = 2 с. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.

Решение. Для построения векторной диаграммы сложения двух колебаний одного направления надо фиксировать какой-либо момент времени. Обычно векторную диаграмму строят для момента времени t = 0. Преобразовав оба уравнения к канонической форме

х = A cos(wt+j), получим

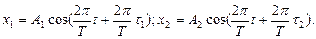
Отсюда видно, что оба складываемых гармонических колебания имеют одинаковую циклическую частоту

.

Начальные фазы первого и второго колебаний соответственно равны

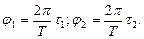
Произведем вычисления:

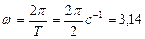с^-1;

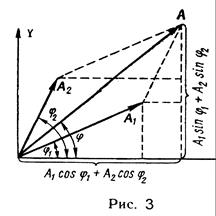
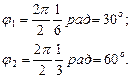
Изобразим векторы А₁ и А₂. Для этого отложим отрезки длиной А₁ = 3 см и А₂ = 2 см под углами j₁ = 30^о и j₂ = 60^о к оси 0х. Результирующее колебание будет происходить с той же частотой w и амплитудой А, равной геометрической сумме амплитуд А₁ и А₂:А = А₁ + А₂. Согласно теореме косинусов:

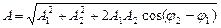
Начальную фазу результирующего колебания можно также определить непосредственно из векторной диаграммы (рис. 3):

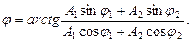
Произведем вычисления:

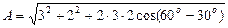см = 4,84 см;

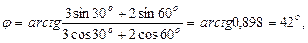
или j = 0,735 рад.

Так как результирующее колебание является гармоническим, имеет ту же частоту, что и слагаемые колебания, то его можно записать в виде

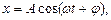
где А = 4,84 см, w = 3,14 с^-1, j = 0,735 рад.