Вычисление потенциальной энергии.
При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними.
Известно, что при статическом растяжении или сжатии стержня силами Р величина работы 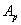 , а следовательно, и величина энергии U равняется:
, а следовательно, и величина энергии U равняется:

В случае сдвига

При кручении

Так же как и при кручении, может быть вычислена потенциальная энергия при чистом изгибе.
Концевые сечения балки под действием изгибающих моментов(Рис.1) повернутся на угол  , где
, где  — центральный угол изогнувшейся по дуге радиусом р оси балки.
— центральный угол изогнувшейся по дуге радиусом р оси балки.

Рис.1. Модель расчета потенциальной энергии при чистом изгибе.
Тогда

так как из общей теории изгиба  а
а 
Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению того сечения, где эта сила приложена. Условимся называть термином «обобщенная сила» всякую нагрузку, вызывающую соответствующее нагрузке перемещение, т. е. и сосредоточенную силу, и пару сил, и т. п.; перемещение же, соответствующее этой силе, будем называть «обобщенной координатой».
«Соответствие» заключается в том, что речь идет о перемещении того сечения, где приложена рассматриваемая сила, причем о таком перемещении, что произведение его на эту силу дает нам величину работы; для сосредоточенной силы это будет линейное перемещение по направлению действия силы — прогиб, удлинение; для пары сил — это угол поворота сечения по направлению действия пары.
Иначе: потенциальная энергия деформации численно равна половине произведения обобщенной силы на соответствующую ей координату.
 ,
,
где Р—обобщенная сила, 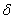 — обобщенная координата.
— обобщенная координата.
Полученные соотношения также показывают, что потенциальная энергия является функцией второй степени от независимых внешних сил, так как в эти формулы не входят реакции, зависящие от приложенных к элементу сил и связанные с ними уравнениями равновесия. Из тех же формул видно, что величина потенциальной энергии деформации является функцией второй степени от «обобщенных координат» системы и вполне ими определяется. Таким образом, порядок приложения нагрузок в этом отношении безразличен, важна лишь окончательная форма деформированного элемента. Поэтому, хотя результаты этого параграфа получены в предположении, что нагрузка возрастает статически, при сохранении равновесия в течение всего процесса нагружения, однако выведенные формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы значения сил и деформаций были связаны линейной зависимостью и относились к тому моменту, когда установится равновесие конструкции.
Известно также, что в общем случае изгиба изгибающий момент М(х) является величиной переменной. В любом сечении ему будет сопутствовать поперечная сила Q(х). Поэтому рассматривать следует уже,не всю балку в целом, а лишь бесконечно малый элемент балки длиной dx.

Рис.2. Энергетическая модель поперечного изгиба
Под действием изгибающих усилий сечения элемента (рис.2, а) поворачиваются и образуют между собой угол 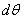 (Рис.2, б). Касательные же усилия стремятся вызвать (Рис.2, в) перекос элемента; таким образом перемещения от нормальных напряжений идут перпендикулярно к направлению касательных напряжений, и наоборот.
(Рис.2, б). Касательные же усилия стремятся вызвать (Рис.2, в) перекос элемента; таким образом перемещения от нормальных напряжений идут перпендикулярно к направлению касательных напряжений, и наоборот.
Это позволяет независимо вычислять работу изгибающих и касательных усилий.
Обычно работа касательных усилий оказывается малой по сравнению с работой нормальных, поэтому мы пока ею будем пренебрегать. Элементарная работа нормальных усилий (как и в случае чистого изгиба) равна:

или


Рис.3. Расчетная схема примера расчета потенциальной энергии при поперечном изгибе.
Вся потенциальная энергия изгиба получится суммированием по длине балки

Знак предела интегрирования условно указывает, что интегрирование должно охватить всю балку; в тех случаях, когда для М(х) мы имеем несколько участков, то интеграл приходится разбивать на сумму интегралов.
Вычислим потенциальную энергию балки на двух опорах, нагруженной силой Р (Рис.3). Эпюра моментов имеет два участка; поэтому




Лекция № 33. Теорема Кастильяно.
Установим теперь метод определения перемещений, основанный на вычислении потенциальной энергии деформации. Поставим задачу нахождения перемещений точек упругой системы по направлению действия приложенных к этой системе внешних сил.
Будем решать эту задачу в несколько приемов; сначала рассмотрим более простой случай (Рис.1), когда на балку в сечениях 1, 2, 3,... действуют только сосредоточенные силы 
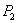 ,
, 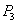 )... и т. д. Под действием этих сил балка прогнется по кривой
)... и т. д. Под действием этих сил балка прогнется по кривой 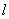 и останется в равновесии.
и останется в равновесии.
Прогибы сечений 1, 2, 3,..., в которых приложены силы 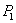 ,
, 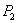 ,
, 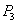 ,..., обозначим
,..., обозначим 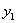 ,
, 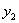 ,
, 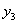 ,... и т. д. Найдем один из этих прогибов, например
,... и т. д. Найдем один из этих прогибов, например 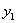 — прогиб сечения, в котором приложена сила
— прогиб сечения, в котором приложена сила 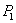 .
.
Переведем балку, не нарушая равновесия, из положения 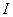 в смежное положение
в смежное положение 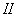 , показанное на фиг. 328 пунктиром. Это можно сделать различными приемами: добавить новую нагрузку, увеличить уже приложенные и т. д.
, показанное на фиг. 328 пунктиром. Это можно сделать различными приемами: добавить новую нагрузку, увеличить уже приложенные и т. д.
Мы представим себе, что для перехода к смежному деформированному состоянию 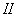 к силе
к силе 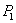 сделана бесконечно малая добавка
сделана бесконечно малая добавка 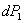 (Рис.1); чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.
(Рис.1); чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.

