Пример решения задания №1
Задача №1.
Цель работы – найти все корни уравнения f(x)= 0 на отрезке [-10, 10]. Варианты уравнений приведены в табл. 1.1. На первом этапе следует отделить корни. Для этого нужно вычислить значения функции y = f(x) на отрезке [-10,10] с шагом H = 0,5 и зафиксировать отрезки [aj,bj] на концах которых функция меняет свой знак. Для каждого варианта нужно построить график функции и таблицу ее значений на отрезке [-10,10] с шагом 0,5. После- отделения корней следует уточнить корни одним из следующих методов с точностью ε = 0,001.
1) половинного деления,
2) хорд,
3) Ньютона,
4) простой итерации.
На каждой итерации в одну строку печатать k, xk, f (xk,) . Критерием окончания итерационного процесса является выполнение условия: ïf( xk)ï< ε
Таблица 1.1
| вариант | уравнение |
| 2х4 -8х3+8х2-1 = 0 | |
| х4- 4х3 -8х2+1 = 0 | |
| х2 – sin5x = 0 | |
| argtgx – 1\3x3 = 0 | |
| 2x3 – 9x2 – 60x + 1 = 0 | |
| e-x = 0,5 + √|x| | |
| (x2 – 1) lg(x+11) = 1 | |
| 3sin√|x| - 0,35x + 3,8 = 0 | |
| x4 -3sinx = 0 | |
| x – 4sinx = 1 |
Задача №2. Приближение функций интерполяционными многочленами
Задание:1) Для функции 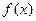 , заданной аналитически на интервале [a; b], и узлов интерполяции с шагом h вычислить в точке х*: значения сплайна S3(x), многочлена Лагранжа L3(x) и функции
, заданной аналитически на интервале [a; b], и узлов интерполяции с шагом h вычислить в точке х*: значения сплайна S3(x), многочлена Лагранжа L3(x) и функции 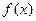 .
.
2) Сравнить полученные результаты вычислений S3(x*), L3(x*) и 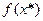 .
.
3) Найти абсолютную и относительную погрешности приближения 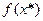 сплайном и многочленом Лагранжа.
сплайном и многочленом Лагранжа.
Вычисления производить с точностью до 0,0001.
Варианты приведены в табл.2.1.
Таблица 2.1
| № | Функция | Интервал | Шаг h | х* |
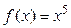 | 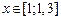 | 0,1 | 1,23 | |
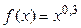 | 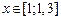 | 0,1 | 1,12 | |
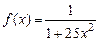 | 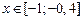 | 0,2 | -0,45 | |
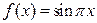 | 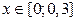 | 0,1 | 0,12 | |
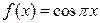 | 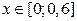 | 0,2 | 0,25 | |
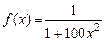 | 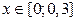 | 0,1 | 0,12 | |
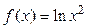 | 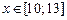 | 11,5 | ||
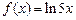 | 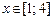 | 2,7 | ||
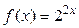 | 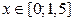 | 0,5 | 0,7 | |
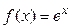 | 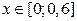 | 0,2 | 0,5 |
Задача №3. Численное дифференцирование
Используя интерполяционные формулы Ньютона и Лагранжа, вычислить 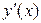 и
и 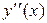 в точках
в точках 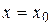 и
и 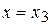 для функции
для функции 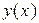 , заданной таблицей
, заданной таблицей
| x | 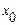 | 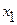 | 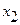 | 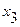 |
| y | 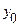 | 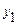 | 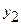 | 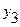 |
Сравнить значения производных 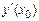 и
и 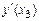 , полученных по разным интерполяционным формулам. Построить график функции
, полученных по разным интерполяционным формулам. Построить график функции 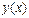 и касательные к нему в точках
и касательные к нему в точках 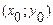 и
и 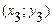 .
.
Варианты приведены в таблице 3.1
| 1. | х | x0= 2 | x3= 5 | 2. | x | x0= 3 | x3= 6 | ||||
| у | 0,6931 | 1,0986 | 1,3863 | 1,6094 | y | 1,0986 | 1,3863 | 1,6094 | 1,7917 | ||
| 3. | x | x0= 4 | x3= 7 | 4. | x | x0= 5 | x3 = 8 | ||||
| y | 1,3863 | 1,6094 | 1,7917 | 1,9459 | y | 1,6094 | 1,7917 | 1,9459 | 2,0794 | ||
| 5. | x | x0= 6 | x3= 9 | 6. | x | x0= 7 | x3= 10 | ||||
| y | 1,7917 | 1,9459 | 2,0794 | 2,1972 | y | 1,9459 | 2,0794 | 2,1972 | 2,3026 | ||
| 7. | x | x0= 11 | x3= 14 | 8. | x | x0=12 | x3 = 15 | ||||
| y | 0,3010 | 0,4771 | 0,6020 | 0,6989 | y | 0,4771 | 0,6020 | 0,6989 | 0,7781 | ||
| 9. | x | x0= 13 | x3= 16 | 10. | x | x0= 14 | x3= 17 | ||||
| y | 0,6020 | 0,6989 | 0,7781 | 0,8451 | y | 0,6989 | 0,7781 | 0,8451 | 0,9031 |
Методические указания и типовые задачи
Пример решения задания №1.
Пусть требуется решить уравнение : x + cos ( x2 + 2) = 0 с точность Ɛ = 0,001 в среде Microsoft Excel.
Составляем таблицу значений функции на интервале [-10, 10] с шагом Н = 0,5 с целью определения отрезков, на которых функция меняет свой знак.
| х | х2 + 2 | cos ( x2 + 2) | x + cos ( x2 +2) | |
| -10 | 0,1016 | -9,8984 | ||
| -9,5 | 92,25 | -0,4141 | -9,9141 | |
| -9 | 0,2495 | -8,7505 | ||
| -8,5 | 74,25 | 0,4101 | -8,0899 | |
| -8 | -0,9996 | -8,9996 | ||
| -7,5 | 58,25 | -0,1302 | -7,6302 | |
| -7 | 0,7422 | -6,2578 | ||
| -6,5 | 44,25 | 0,9644 | -5,5356 | |
| -6 | 0,9551 | -5,0449 | ||
| -5,5 | 32,25 | 0,6719 | -4,8281 | |
| -5 | -0,2921 | -5,2921 | ||
| -4,5 | 22,25 | -0,9667 | -5,4667 | |
| -4 | 0,6603 | -3,3397 | ||
| -3,5 | 14,25 | -0,1126 | -3,6126 | |
| -3 | 0,0044 | -2,9956 | ||
| -2,5 | 8,25 | -0,3857 | -2,8857 | |
| -2 | 0,9602 | -1,0398 | ||
| -1,5 | 4,25 | -0,4461 | -1,9461 | |
| -1 | -0,9900 | -1,9900 | ||
| -0,5 | 2,25 | -0,6282 | -1,1282 | |
| -0,4161 | -0,4161 | |||
| х | х2 + 2 | cos ( x2 + 2) | x + cos ( x2 + 2) | |
| 0,5 | 2,25 | -0,6282 | -0,1282 | |
| -0,9900 | 0,0100 | |||
| 1,5 | 4,25 | -0,4461 | 1,0539 | |
| 0,9602 | 2,9602 | |||
| 2,5 | 8,25 | -0,3857 | 2,1143 | |
| 0,0044 | 3,0044 | |||
| 3,5 | 14,25 | -0,1126 | 3,3874 | |
| 0,6603 | 4,6603 | |||
| 4,5 | 22,25 | -0,9667 | 3,5333 | |
| -0,2921 | 4,7079 | |||
| 5,5 | 32,25 | 0,6719 | 6,1719 | |
| 0,9551 | 6,9551 | |||
| 6,5 | 44,25 | 0,9644 | 7,4644 | |
| 0,7422 | 7,7422 | |||
| 7,5 | 58,25 | -0,1302 | 7,3698 | |
| -0,9996 | 7,0004 | |||
| 8,5 | 74,25 | 0,4101 | 8,9101 | |
| 0,2495 | 9,2495 | |||
| 9,5 | 92,25 | -0,4141 | 9,0859 | |
| 0,1016 | 10,1016 |
Из полученной таблицы следует, что только на интервале [0,5; 1] функция меняет свой знак, т е корень уравнения находится внутри этого интервала.
a) Применим метод половинного деления
| a | b | f(a) | f(b) | (a+b)/2 | f((a+b)/2) |
| 0,5 | -0,1282 | 0,0100 | 0,75 | -0,0870 | |
| 0,75 | -0,0870 | 0,0100 | 0,875 | -0,0552 | |
| 0,875 | -0,0552 | 0,0100 | 0,9375 | -0,0282 | |
| 0,9375 | -0,0282 | 0,0100 | 0,9688 | -0,0107 | |
| 0,9688 | -0,0107 | 0,0100 | 0,9844 | -0,0008 | |
| 0,9844 | -0,0008 | 0,0100 | 0,9922 | 0,0045 | |
| 0,9844 | 0,9922 | -0,0008 | 0,0045 | 0,9883 | 0,0019 |
| 0,9844 | 0,9883 | -0,0008 | 0,0019 | 0,9864 | 0,0006 |
| 0,9844 | 0,9864 | -0,0008 | 0,0006 | 0,9854 | -0,0001 |
| 0,9854 | 0,9864 | -0,0001 | 0,0006 | 0,9859 | 0,0002 |
Т.к. |0,9854 - 0,9859| < 0, 001, то процесс закончен и х ≈ 0, 985.
b) Применим метод хорд. Вычисляем первое приближение к корню по формуле:
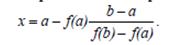
где а = -10 и b = 10.
1. x = -10 – (-9,8984)* ( 10 +10) \ (10,1016 + 9,8984) = - 0, 1016. Т.к заданная точность не достигнута ( f(x) = -0,5271 по модулю больше, чем 0,001) , то продолжаем процесс, вычисляя следующее значение корня х при а = - 0, 1016 и b = 10:
2. x = - 0, 1016 – (-0,5271)* ( 10+ 0, 1016)\( 10,1016 + 0,5271) ≈ 0,39936
f (0,39936) = -0,1559, что недостаточно точно, т к |-0,1559|>0,001
а = 0,39936 и b = 10
3. x = 0,39936 – (-0,1559) * ( 10 - 0,39936) (10,1016 + 0,1559) ≈ 0,54527
f (0,54527) = -0,1190, |-0,1190| > 0,001
a = 0,54527 и b = 10
4. x = 0,54527 – (-0,1190)* ( 10 - 0,54527)\ (10,1016 +0,1190) ≈ 0,65533
f (0, 65533) = -0,1016
a = 0,65533 и b = 10
5. x = 0,65533 – (-0,1016) * (10 -0,65533 )\( 10,1016 + 0,1016) ≈ 0,74838
f(x) = -0,0872
a = 0,74838 и b = 10
6. x = 0,74838 – (-0,0872)*(10 - 0,74838)\( 10,1016 +0,0872) ≈ 0,82756
f(x) = -0,0699
a = 0,82756 и b = 10
7. x = 0,82756 – (-0,0699)* (10-0,82756)\( 10,1016 +0,0699) ≈ 0,89041
f(x) = - 0,0494
a = 0, 89041 и b = 10
8. x = 0, 89041- (- 0,0494)*(10 - 0, 89041)\ (10,1016 + 0,0494) ≈0,93975
f(0,93975) = -0,0207
a = 0,93975 и b = 10
9. x = 0,93975 – (-0,0207)* ( 10 - 0,93975) \ (10,1016 + 0,0207) ≈ 0,95829
f (0,95829) = - 0,0169
a= 0,95829 и b = 10
10. x = 0,95829 – (- 0,0169)*(10- 0,0169)\(10,1016 + 0,0169) ≈ 0,97496
f(x) = - 0,0068
a = 0,97496 и b = 10
11. x = 0,97496- (- 0,0068) (10 - 0,97496)\(10,1016 + 0,0068) ≈ 0,98103
f(x) = -0,0030
a = 0,98103 и b = 10
12. x = 0,98103 – (0,0030)* (10 - 0,98103)\ (10,1016 + 0,0030) ≈ 0,98371
f(0,98371) = -0,0012
a = 0,98371 и b = 10
13. x = 0,98371 - (-0,0012)*(10- 0. 98371)\(10,1016+ 0,0012) ≈ 0,98478
f(0,98478) = -0,0005 – заданная точность достигнута: f(x) < 0,001
х ≈ 0, 985
с) Применим метод Ньютона.Найдем начальную точку по формуле:
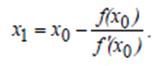
f' (x) = 1 – sin(x2 +2) * 2x
Тк из ранее полученных результатом, мы знаем в каком отрезке находится корень, для уменьшения вычислений возьмем в качестве х0 = 2. Получим таблицу:
| x | x2 + 2 | f(x)= x + cos ( x2 + 2) | f' (x) = 1 – sin(x2 +2) * 2x | хi |
| 6,00000 | 2,96017 | 2,11766 | 0,60215 | |
| 0,60215 | 2,36258 | -0,10946 | 0,15389 | 1,31344 |
| 1,31344 | 3,72512 | 0,47892 | 2,44734 | 1,11775 |
| 1,11775 | 3,24937 | 0,12355 | 1,24046 | 1,01815 |
| 1,01815 | 3,03663 | 0,02365 | 0,78666 | 0,98808 |
| 0,98808 | 2,97630 | 0,00171 | 0,67484 | 0,98555 |
| 0,98555 | 2,97131 | 0,00001 | 0,66597 | 0,98553 |
| 0,98553 | 2,97127 | 0,00000 | 0,66590 | 0,98553 |
Достигнута нужная точность и найден корень уравнения : х = 0.985.
