Випуск продукції підприємством за рік

Вирівнювання динамічних рядів

Динаміка ряду вивчається в трьох аспектах: тенденція (довготривалий рух), короткочасний систематичний рух і несистематичний випадковий рух. З цією метою ряди динаміки піддають менш чи більш складній обробці.

Найпростіший спосіб обробки ряду з метою виявлення закономірності зміни його рівня полягає у визначенні підсумкових або середніх показників для збільшених інтервалів часу.

Ø Наприклад, є наступні дані, що відображають випуск продукції на підприємстві по місяцях за рік.

Таблиця

Випуск продукції підприємством за рік

Місяці	Випуск продукції, млн. грн.	Місяці	Випуск продукції, млн. грн.
Січень Лютий Березень Квітень Травень Червень	5,1 5,4 5,2 5,3 5,6 5,8	Липень Серпень Вересень Жовтень Листопад Грудень	5,6 5,9 6,1 6,0 5,9 6,2

Збільшимо інтервали до 3-х місяців і розрахуємо загальний і середньомісячний випуски продукції по кварталах. Нові дані будуть виглядати наступним чином (табл. ).

Таблиця

Випуск продукції підприємством за рік

Квартали	Випуск продукції, млн. грн.	Середньомісячний випуск продукції по кварталах, млн. грн.
I II III IV	15,7 16,7 17,6 18,1	5,23 5,57 5,87 6,03

Як показує приклад, новий ряд більш чітко відображає загальну закономірність збільшення випуску продукції.

Доволі часто при обробці динамічного ряду з метою визначення тенденції розвитку застосовують вирівнювання способом плинної середньої. За цим способом фактичні рівні замінюються рядом плинних середніх, які розраховуються для визначених послідовно плинних інтервалів і є центром кожного з них.

Приклад розрахунку ілюструє таблиця яка характеризує виробництво чавуну на підприємстві у 1986 – 2000 роках.

Таблиця

Виробництво чавуну на підприємстві 1982 – 1996 роках

Роки	Валове виробництво чавуну (млн. т)	Плинна сума 5 членів ряду	Плинна середня 5 членів ряду
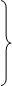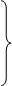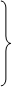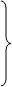1986	7,3 7,1 6,9 5,7 5,9 6,0 6,0 5,7 5,3 5,2 4,3 4,5 4,3 4,6 4,3	– – 32,9 31,6 30,5 29,3 28,9 28,2 26,5 25,0 23,6 22,9 22,0 – –	– – 6,58 6,32 6,10 5,86 5,78 5,64 5,30 5,00 4,72 4,58 4,4 – –

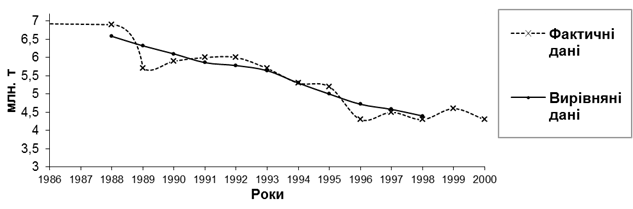
Рис. 9.2. Вирівняні і фактичні дані про валове виробництво чавуну у 1986 - 2000 роках

Ефект вирівнювання, що усуває коливання рівнів за рахунок випадкових причин і виявляє загальну закономірність розвитку, наочно представлений графічним зображенням фактичних і вирівняних даних.

Більш удосконаленим способом обробки динамічних рядів з метою встановлення тенденції розвитку явищ є вирівнювання за аналітичними формулами.

За цим способом на основі фактичних даних ряду підбирається найбільш придатна для відображення тенденції розвитку явища математична формула (функція), за якою і розраховують вирівняні значення.

Іншими словами, рівні ряду розглядаються як функція часу (y = f(t)), і завдання вирівнювання зводиться до визначення виду функції, пошуку її параметрів за емпіричними даними і розрахунку теоретичних рівнів за знайденою формулою. Найпростішими формулами, що відображають тенденцію розвитку (тренд), є: аналітична пряма 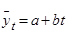, показникова функція 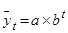, парабола 2-го порядку 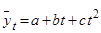, гіпербола 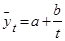, де 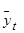– теоретичний рівень (читається: “ігрек”, вирівняний за t), t – часові точки, а, b – параметри прямої.

Вирівнювання за рівнянням прямої є ефективним, як правило, тоді, коли абсолютні прирости більш-менш постійні, тобто коли рівні ряду змінюються в арифметичній прогресії (або наближено до неї).

Параметри а і b прямої знаходяться шляхом розв’язування системи нормальних рівнянь, отриманих за способом найменших квадратів:

,

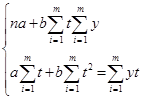де у – рівні емпіричного ряду, п – кількість рівнів ряду, t – часові точки (роки, місяці).

Цю систему легко спростити, якщо часові точки (t) умовно позначити так, щоб їх сума дорівнювала нулю. Для цього відлік часових точок ведеться від центру ряду. При непарній кількості рівнів ряду середня часова точка (рік, місяць) приймається за нуль, тоді попередні періоди позначаються відповідно через –1, –2, –3 і т. д., а наступні за середнім періоди – відповідно через +1, +2, +3 і т. д.

При парній кількості рівнів ряду дві середні часові точки позначаються через –1 та +1 (тобто між ними береться два умовних інтервали –1, 0, +1), і тоді інші часові точки умовно позначаються через два інтервали.

Якщо å t = 0, то попередня система рівнянь приймає наступний вигляд:

,

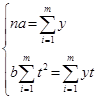звідки

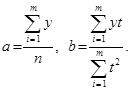
Проведемо вирівнювання на прикладі динамічного ряду, що характеризує виплавку сталі в регіоні за 1995 – 2000 роки (табл.).

Таблиця

Розрахункова таблиця вирівнювання динамічного ряду

Роки	Виплавка сталі, тис. т (у)	Часові точки (t)	(t2)	(уt)	Вирівняні рівні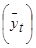
	115,9 110,3 106,5 102,2 96,9 91,0	–5 –3 –1 +1 +3 +5		–579,5 –330,9 –106,5 102,2 290,7 455,0	115,8 111,0 106,2 101,4 96,6 91,8
å	622,8			–169,0	622,8

Розглядаючи рівні ряду як функцію часу, припустимо, що розвиток у часі може бути відображений аналітичною прямою. Позначивши часові точки (роки) так, щоб åt = 0, розрахуємо в таблиці необхідні для розв’язку системи рівнянь п, åу, åt², åуt.

Використовуючи підраховані підсумки, визначаємо:

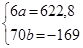
Звідси: а = 103,8; b = –2,4; 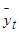= 103,8 – 2,4t.

Підставляючи в дане рівняння послідовно значення t = –5, –3, –1, 1, +3, +5, знаходимо вирівняні рівні.