Теорема Умножения вероятностей
Т. ~Р(АВ)=Р(А)Ра(В) ~Р(АВС)=Р(А)Ра(В)Рав(С). Следствие. А и В независимы ó Р(АВ)=Р(А)Р(В), т.е. в частности вер-ть произведений 2-х независимых событий равна произведению их вер-стей. Теорема для независимых вер-тей.=> Р(В1)Р(`В2)+Р(`В1)Р(В2). Пр.: Два стрелка одновременно выстреливают в мишень. Вер-ть попадания для 1-го =0,6; для 2-го 0,8.; Найти: А)Вер-ть того что в мишени будет 1 пробоина. В)будет хотя бы одна пробоина. Реш.: В мишени будет 1 пробоина т.ит.т.к. 1-ый попал и 2-ой промахнулся, 1-ый промахнулся и 2-ой попал.
А=(В1`В2+`В1В2)=Р(В1`В2)+Р(`В1В2). Используем терему для независ. вер-тей.
Р(В1)=0,6; Р(`В1)=1-0,6=0,4; Р(В2)=0,8; Р(`В2)=0,2.; Р(А)=0,6×0,2+0,4×0,8=0,44.
ХОТЯБЫ 1 => Р(с)=Р(А+D) {D-2-е попадание} P(D)=P(B1×B2)=P(B1)P(B2)=
=0,6×0,8=0,48.; P(c)=0,92.
Формула полной вер-ти.
Т. Пусть события А1,А2,…Ак – образуют полную систему и F-некотор. Событие, тогда вер-ть этого события может быть найдена по след. ф-ле: P(F)=P(A1)Pa1(F)++P(A2)Pa2(F)+…P(Ak)Pak(F) Пусть дополнительно событие F отлично от невозможного PF(Ai)=(P(Ai)×Pai(F)/ P(F) ) –формула гипотезы, где 1£i£к. Пр.: (в тетради на стр.17-18).
Тема: Повторные независимые испытания.
Формула Бернулли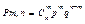 
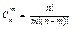Теорема: Пусть проведено “n” повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вер-тью р. Тогда вер-ть Pm,n что в этих испытаниях событие А будет n раз выполняться по формуле.
Формула Пуассона (редких событий).
Теорема. Пусть проведено n повторных независимых испытаний, в каждом из которых события А наступает с вер-тью р, причем 1)число испытаний достаточно велико (n³100) 2)Величина l=np£10, тогда вер-ть Pm,n того, что в этих испытаниях событие А наступит m раз вычисл. по след. приближ. ф-ле:
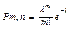
Локальная теорема Муавра – Лапласа.
Теорема: Пусть проведено n повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вер-тью р., причем. 1)число испытаний достаточно велико 2)npq³10, где q=1-р, тогда вер-ть Рm,n того, что в этих n испытаниях событие А наступит m раз вычисляется по ф-ле:
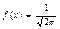
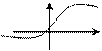
Свойства функции Гаусса: 1)Четность f(-x)=f(x); 2)Не отрицательность f(x)>0; 3) lim f(x)=lim f(x)=0 {при хà¥}; Практическое правило: если х³5,то будем полагать, что f(x)»0. {Далее следует график y=f(x) в виде «горки»}
Интегральная теорема Муавра-Лапласа.
Т.: Пусть проведено n повторных независимых испытаний, в каждом из которых некоторое событие А наступает с вер-тью р, причём. 1)число испытаний достаточно велико. 2)Значение npq³20. ; Тогда вер-ть того, что число m наступлений событий А в этих испытаниях окажется заключено в границах от m1 до m2 вычисляется по
след. приближ. ф-ле.
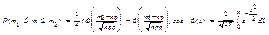
Св-ва функции Лапласа.
1)Нечётность Ф(-х)=-Ф(х);
2)Монотонно возрастающая Ф(х);
3)limФ(х)=1 {где хà+¥}; limФ(x)=-1 {где хà-¥}. На практике: если х³5, полагаем что Ф(х)»1 График у=Ф(х) в пределах от –1 до 1.
