Iv. аналитическая геометрия в пространстве
Примерные задачи для подготовки к экзамену по дисциплине
«ЛИНЕЙНАЯ АЛГЕБРА»
I. СЛАУ
- Решить систему уравнений
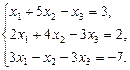
а) с помощью формул Крамера; б) с помощью обратной матрицы; в) методом Гаусса.
- Исследовать систему на совместность, в случае совместности указать число базисных и число свободных неизвестных, найти решение:
а) 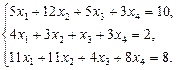 б)
б) 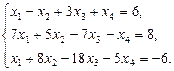
- Определить, при каком значении параметра
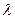 система однородных линейных уравнений имеет множество решений (неопределенна) и решить систему при найденном
система однородных линейных уравнений имеет множество решений (неопределенна) и решить систему при найденном 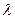
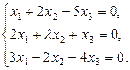
- Вычислить определитель по теореме о разложении; найти произведение матриц, элементами которых являются элементы миноров
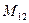 и
и 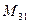
а) 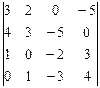 б)
б) 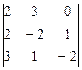
- Вычислить: а) ранг матрицы С =А * В
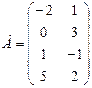 ,
, 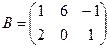
б) r(A), если А= 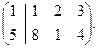
- Решить матричные уравнения
а) 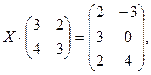 б)
б) 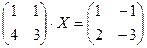 .
.
Указание: 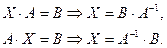
- Вычислить определитель матрицы
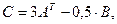 если
если
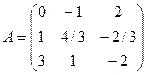
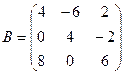
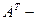 транспонированная матрица А.
транспонированная матрица А.
- Найти
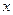 из уравнения а)
из уравнения а) 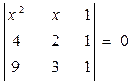 ; б)
; б) 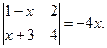
- Для матрицы
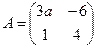 не существует обратной матрицы при а=?
не существует обратной матрицы при а=?
II. ВЕКТОРНАЯ АЛГЕБРА
- Даны точки А(3; -7; 4) и В(0; -5; -2). Найти координаты и длину вектора АВ.
- Найти координаты и длину вектора
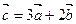 , если
, если 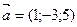 и
и 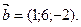
-
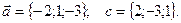 Если
Если 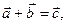 то
то 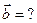
- Определить, при каких значениях
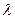 векторы
векторы 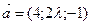 и
и 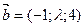 будут ортогональными (перпендикулярными).
будут ортогональными (перпендикулярными). - Определить, при каких значениях
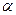 и
и 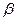 вектора
вектора 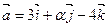 и
и 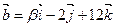 будут коллинеарными?
будут коллинеарными? - Даны векторы
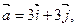
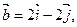
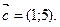 Разложить вектор
Разложить вектор 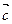 через векторы
через векторы 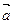 и
и 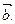
- Найти косинус угла между векторами
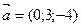 и
и 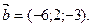
- Найти проекцию вектора
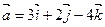 на вектор
на вектор 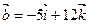
- В плоскости находятся два вектора
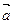 и
и 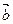 . Даны модули этих векторов
. Даны модули этих векторов 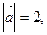
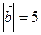 и угол между ними
и угол между ними 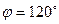 . Найти скалярное произведение этих векторов и модуль вектора
. Найти скалярное произведение этих векторов и модуль вектора 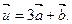
-
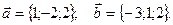 Найти координаты вектора
Найти координаты вектора 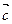 , который перпендикулярен и вектору
, который перпендикулярен и вектору 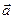 и вектору
и вектору 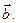
III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- Составить общее уравнение прямой на плоскости, проходящей через точки А(-3, 5) и В(1, 3).
- Составить уравнение прямой на плоскости, проходящей через точку пересечения прямых 2х +2y =5 и 3x – y = 1.5, которая а) параллельна прямой y = 5x + 3, б) перпендикулярна прямой y = 2x – 5.
- Составить уравнение медианы АМ и высоты ВК треугольника АВС, если А(-3;3), В(2;4) ,С(0;-1).
- Составить уравнение окружности, диаметром которой является отрезок АВ, где А(6;4), В(4; -2).
- Уравнение окружности с центром в точке С(-3;1) и радиусом R=2 имеет вид…
- Написать уравнение прямой, проходящей через центр окружности
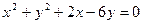 перпендикулярно прямой
перпендикулярно прямой 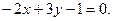
- Составить каноническое уравнение гиперболы, мнимая ось которой равна 4 а уравнения асимптот имеют вид
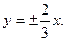
- Найти координаты фокусов, длины осей, эксцентриситет
а) эллипса 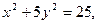 б) гиперболы
б) гиперболы 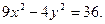 Записать уравнения асимптот.
Записать уравнения асимптот.
- Составить каноническое уравнение эллипса, если расстояние между его фокусами равно
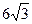 а длинна большой оси равна 12. Построить эллипс, указать его вершины и эксцентриситет.
а длинна большой оси равна 12. Построить эллипс, указать его вершины и эксцентриситет.
IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- Плоскости
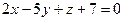 и
и 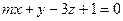 перпендикулярны, если m=?
перпендикулярны, если m=? - Составит уравнение плоскости, проходящей через точку
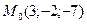 параллельно плоскости
параллельно плоскости 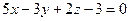 .
. - Составит уравнение плоскости, которая проходит через точку
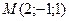 , перпендикулярно двум плоскостям
, перпендикулярно двум плоскостям 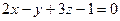 и
и 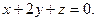
- Составить уравнение плоскости, проходящей через три точки
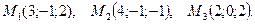
- Среди плоскостей
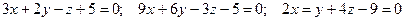 указать параллельные и перпендикулярные.
указать параллельные и перпендикулярные. - Определить угол между двумя плоскостями
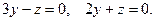
- Составить каноническое уравнение прямой, проходящей через точку
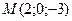 параллельно: а) вектору
параллельно: а) вектору 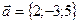 ; б) прямой
; б) прямой 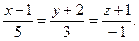
- Составит параметрическое уравнение прямой, проходящей через точку
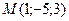 параллельно вектору
параллельно вектору 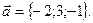
- Центр сферы
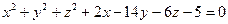 имеет координаты?
имеет координаты? - Вершина конуса
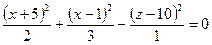 имеет координаты?
имеет координаты?
РАЗНОЕ
- Потребитель тратит весь свой доход на потребление двух благ А и В. В таблице приведены ежемесячные данные об объемах потребления и динамике изменения дохода потребителя по отношению к предыдущему месяцу:
| месяцы | потребление | Доход потребителя (у.е) | |
| Благо А(ед) | Благо В(ед) | ||
| январь | |||
| февраль | Увелич на 20% | ||
| март | Увелич на 25% |
Найти отношение стоимости единиц блага А к стоимости единицы блага В?
Указание. x- стоимость единицы блага А, y- стоимость единицы блага В. Доход потребления: январь 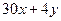 , февраль….., март…….Динамика
, февраль….., март…….Динамика 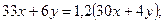 ……..Найти
……..Найти 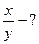
- Потребитель тратит весь свой доход на потребление двух благ А и В. В таблице приведены ежемесячные данные об объемах потребления и динамике изменения дохода потребителя по отношению к предыдущему месяцу:
| месяцы | потребление | Доход потребителя (у.е) | |
| Благо А(ед) | Благо В(ед) | ||
| январь | |||
| февраль | Увелич. на 20% | ||
| март | Уменьш. на 25% |
Найти отношение стоимости единиц блага А к стоимости единицы блага В?
- Потребитель тратит весь свой доход на потребление двух благ А и В. В таблице приведены ежемесячные данные об объемах потребления и динамике изменения дохода потребителя по отношению к предыдущему месяцу:
| месяцы | потребление | Доход потребителя (у.е) | |
| Благо А(ед) | Благо В(ед) | ||
| январь | |||
| февраль | Увелич. на 20% | ||
| март | Уменьш. на 25% |
Если стоимость единицы блага А равна 3 у.е., то доход потребителя в марте изменился на ? у.е.
Указание. Надите 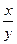 . По условию y=3. Найдете x. Рассчитаете доход в феврале и марте и найдете разницу в доходе вычитанием.
. По условию y=3. Найдете x. Рассчитаете доход в феврале и марте и найдете разницу в доходе вычитанием.
