Разложение в ряд Маклорена элементарных функций.
Стандартные разложения.
1. .
Всё начинается с геометрической прогрессии. На первой лекции по рядам (см. раздел 18.1. Основные определения) мы доказали, что эта функция является суммой ряда 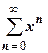 , и ряд сходится к функции при
, и ряд сходится к функции при 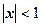 . Итак,
. Итак,
.
Выпишем несколько разновидностей этого ряда. Заменив х на -х, получим
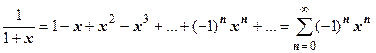 ;
;
при замене х на 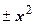 получаем
получаем
 ;
;  ;
;
и т.д.; область сходимости всех этих рядов одна и та же: 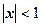 .
.
2. 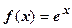 .
.
Все производные этой функции в точке х=0 равны 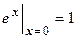 , поэтому ряд имеет вид
, поэтому ряд имеет вид
 .
.
Область сходимости этого ряда - вся числовая ось (пример 6 раздела 18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда), поэтому 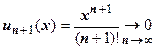 при
при 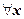 . Как следствие, остаточный член формулы Тейлора
. Как следствие, остаточный член формулы Тейлора 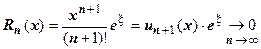 . Поэтому ряд сходится к
. Поэтому ряд сходится к 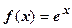 в любой точке х.
в любой точке х.
3. .
Здесь 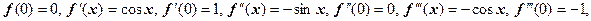
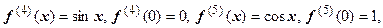 дальше производные периодически повторяются. Ряд Маклорена имеет вид
дальше производные периодически повторяются. Ряд Маклорена имеет вид
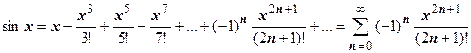 .
.
Этот ряд абсолютно сходится при 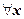
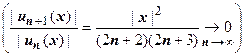 , и его сумма действительно равна
, и его сумма действительно равна 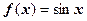 . Остаточный член формулы Тейлора имеетвид
. Остаточный член формулы Тейлора имеетвид 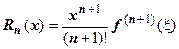 , где
, где 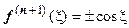 или
или 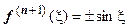 - ограниченная функция, а
- ограниченная функция, а 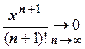 (это общий член предыдущего разложения).
(это общий член предыдущего разложения).
4. .
Это разложение можно получить, как и предыдущие, последовательным вычислением производных, но мы поступим по другому. Почленно продифференцируем предыдущий ряд:
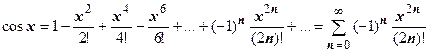 .
.
Сходимость к функции на всей оси следует из теоремы о почленном дифференцировании степенного ряда.
5.Самостоятельно доказать, что на всей числовой оси 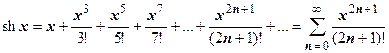 ,
, 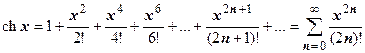 .
.
6. .
Ряд для этой функции называется биномиальным рядом. Здесь мы будем вычислять производные.
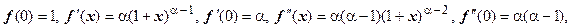
 … Ряд Маклорена имеет вид
… Ряд Маклорена имеет вид
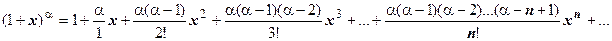
Ищем интервал сходимости: 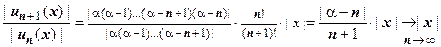 , следовательно, интервал сходимости есть
, следовательно, интервал сходимости есть 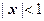 . Исследование остаточного члена и поведение ряда на концах интервала сходимости проводить не будем; оказывается, что при
. Исследование остаточного члена и поведение ряда на концах интервала сходимости проводить не будем; оказывается, что при 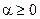 ряд абсолютно сходится в обеих точках
ряд абсолютно сходится в обеих точках 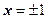 , при
, при 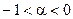 ряд условно сходится в точке
ряд условно сходится в точке 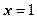 и расходится в точке
и расходится в точке 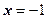 , при
, при 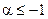 расходится в обеих точках.
расходится в обеих точках.
7. .
Здесь мы воспользуемся тем, что 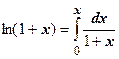 . Так как
. Так как 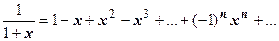 , то, после почленного интегрирования,
, то, после почленного интегрирования,
 .
.
Область сходимости этого ряда - полуинтервал 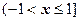 , сходимость к функции во внутренних точках следует из теоремы о почленном интегрировании степенного ряда, в точке х=1 - из непрерывности и функции, и суммы степенного ряда во всех точках, сколь угодно близких к х=1 слева. Отметим, что взяв х=1, мы найдём сумму ряда
, сходимость к функции во внутренних точках следует из теоремы о почленном интегрировании степенного ряда, в точке х=1 - из непрерывности и функции, и суммы степенного ряда во всех точках, сколь угодно близких к х=1 слева. Отметим, что взяв х=1, мы найдём сумму ряда 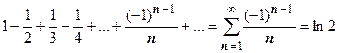 .
.
8.Почленно интегрируя ряд  , получим разложение для функции
, получим разложение для функции  . Выполнить все выкладки самостоятельно, выписать область сходимости.
. Выполнить все выкладки самостоятельно, выписать область сходимости.
9.Выпишем разложение функции 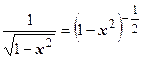 по формуле биномиального ряда с
по формуле биномиального ряда с 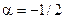 :
: 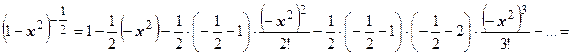
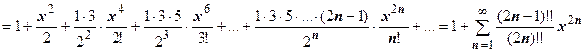 . Знаменатель
. Знаменатель 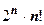 представлен как
представлен как 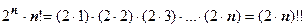 , двойной факториал
, двойной факториал 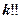 означает произведение всех натуральных чисел той же чётности, что и
означает произведение всех натуральных чисел той же чётности, что и 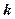 , не превосходящих
, не превосходящих 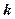 . Разложение сходится к функции при
. Разложение сходится к функции при 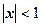 . Почленно интегрируя его от 0 до х, получим
. Почленно интегрируя его от 0 до х, получим 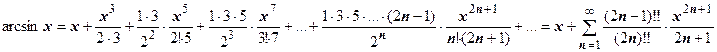 . Оказывается, что этот ряд сходится к функции на всём отрезке
. Оказывается, что этот ряд сходится к функции на всём отрезке  ; при х=1 получаем ещё одно красивое представление числа
; при х=1 получаем ещё одно красивое представление числа 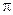 :
: 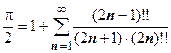 .
.
18.2.6.2. Решение задач на разложение функций в ряд.Большинство задач, в которых требуется разложить элементарную функцию в ряд по степеням  , решается применением стандартных разложений. К счастью, любая основная элементарная функция имеет свойство, которое позволяет это сделать. Рассмотрим ряд примеров.
, решается применением стандартных разложений. К счастью, любая основная элементарная функция имеет свойство, которое позволяет это сделать. Рассмотрим ряд примеров.
1. Разложить функцию 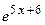 по степеням
по степеням  .
.
Решение. 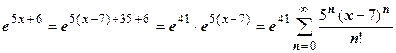 . Ряд сходится при
. Ряд сходится при 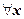 .
.
2. Разложить функцию 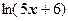 по степеням
по степеням  .
.
Решение. 
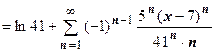 . Область сходимости:
. Область сходимости: 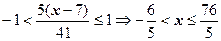 .
.
3. Разложить функцию 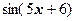 по степеням
по степеням  .
.
Решение. 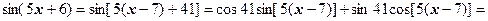
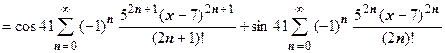 . Ряд сходится при
. Ряд сходится при 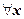 .
.
4. Разложить функцию 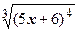 по степеням
по степеням  .
.
Решение. 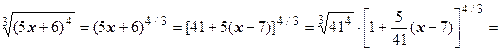
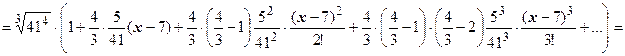
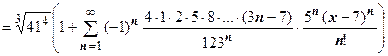 . Ряд сходится при
. Ряд сходится при 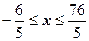 .
.
5. Разложить функцию 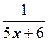 по степеням
по степеням  .
.
Решение. 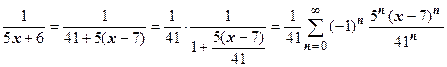 . Область сходимости
. Область сходимости 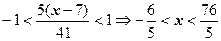 .
.
6. Разложить функцию 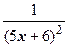 по степеням
по степеням  .
.
Решение. Разложение в ряд простых рациональных дробей второго типа получается почленным дифференцированием соответствующих разложений дробей первого типа. В этом примере 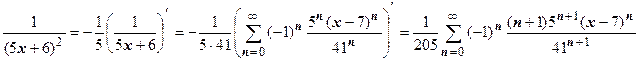 . Дальше почленным дифференцированием можно получить разложения функций
. Дальше почленным дифференцированием можно получить разложения функций  ,
, 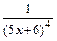 и т.д.
и т.д.
7. Разложить функцию 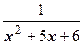 по степеням
по степеням  .
.
Решение. Если рациональная дробь не является простой, она сначала представляется в виде суммы простых дробей: 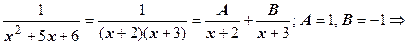
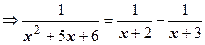 , а затем действуем, как в примере 5:
, а затем действуем, как в примере 5: 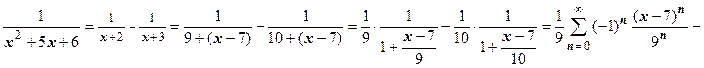
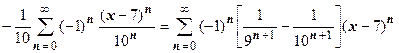 , где
, где  .
.
Естественно, такой подход неприменим, например, для разложения функции 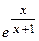 по степеням х. Здесь, если надо получить несколько первых членов ряда Тейлора, проще всего найти значения в точке х=0 требуемого количества первых производных.
по степеням х. Здесь, если надо получить несколько первых членов ряда Тейлора, проще всего найти значения в точке х=0 требуемого количества первых производных.
