| | Наборы двумерных данных содержат информацию о двух признаках (переменных) для каждого из объектов. В дополнение к изучению обобщающих характеристик каждой из этих двух переменных, рассматриваемых как отдельные наборы одномерных данных, статистические методы анализа двумерных данных используются для изучения связи между этими двумя переменными. При таком анализе необходимо выяснить следующие вопросы. Ü Существует ли между этими двумя переменными простая связь? Ü Насколько сильно взаимосвязаны переменные? Ü Можно ли предсказать значение одной переменной на основании другой? Если да, то с какой степенью надежности? Ü Существуют ли отдельные объекты или группа объектов, которые требуют особого внимания? При изучении зависимости между двумя переменными рекомендуется в качестве первоначальной цели провести визуальное исследование. Существует два вида численных анализа двумерных данных, представленных переменными X и Y: корреляционный анализ и ковариационный анализ, позволяющий оценить степень взаимосвязи между переменными X и Y,; регрессионный анализ, определяющий форму (вид) связи между этими переменными. Ниже рассмотрен корреляционный анализ Корреля́ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). Для визуального анализа зависимости между двумя переменными используются графики рассеяния. В Excel данный вид графиков называется точечной диаграммой или диаграммой рассеяния. Диаграмма рассеяния позволяет увидеть структуру двумерных данных. Если ваши данные содержат какие-то проблемы (например, выбросы), чаще всего единственный способ их обнаружения состоит как раз в анализе диаграммы рассеяния. При построении диаграмм рассеяния одна переменная (обозначается буквой Y) рассматривается как зависимая переменная, другая переменная (обозначается буквой X) является независимой переменной, оказывающей влияние на переменную Y. На диаграмме рассеяния переменой X соответствует горизонтальная ось, а переменной Y – вертикальная ось. |
| Подготовить исходные данные | Таблица 1. Объекты анализа | Объект | | | Объект | | | | | | 26,0 | | | 37,2 | | | | 31,0 | | | 38,4 | | | | 37,4 | | | 43,6 | | | | 34,8 | | | 44,8 | | | | 39,2 | | | 40,6 | | | | 38,0 | | | 41,8 | | | | 39,6 | | | 45,2 | | | | 31,2 | | | | |
| Ввести обозначения Независимой и зависимой переменных | X – независимая переменная, определяющая размер 1 (в метрах); Y – зависимая переменная, определяющая параметр 2 (в тысячах долларов). |
| Расположите данные в столбцах | Расположить необходимо таким образом, чтобы значения X были слева, а значения Y – справа |
| Построить диаграмму | Необходимо выбрать тип Точечная диаграмма |
| Выполнить визуальный анализ полученной диаграммы | Визуально можно определить имеется ли между зависимостями взаимосвязь показывает определенную зависимость между переменными. |
| Выполнить корреляционный анализ |
| Изучить теоретическую справку по КЭ | Корреляция, или коэффициент корреляции является распространенной общей характеристикой двумерных данных в том же смысле, в каком среднее и стандартное отклонение являются важными характеристиками для анализа одномерного набора данных. Коэффициент корреляции характеризует «силу (тесноту)» линейнойзависимости между двумя переменными. Возможные значения коэффициента корреляции лежат в диапазоне от –1 до +1. Отрицательный знак коэффициента корреляции указывает на то, что с увеличением значений одной переменной значения другой переменной будут уменьшаться (прямая с отрицательным углом наклона). В случае положительного коэффициента корреляции с увеличением значений одной переменной значения другой переменной также увеличиваются (прямая с положительным углом наклона). Формула для вычисления выборочного коэффициента корреляции имеет вид: 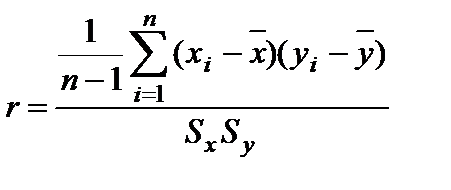 , где , где 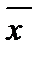 и и 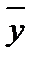 – средние значения переменных X и Y; Sx и Sy – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1. Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер. – средние значения переменных X и Y; Sx и Sy – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1. Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер. |
| Провести корреляционный анализ средствами Excel | Определить коэффициенты корреляции Корреляционный анализ может выполняться двумя способами: Инструментом Анализ данных Мастером функций КОРРЕЛ В отличие от инструмента анализа Корреляция статистическая функция КОРРЕЛ не статична, т.е. при изменении данных в исходном диапазоне значение коэффициента корреляции, рассчитанного с помощью функции КОРРЕЛ, тоже изменится. |
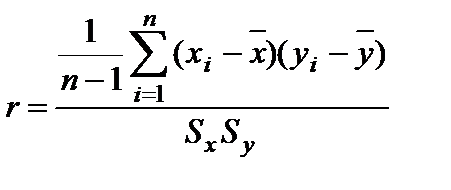 , где
, где 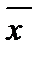 и
и 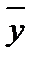 – средние значения переменных X и Y; Sx и Sy – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1. Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер.
– средние значения переменных X и Y; Sx и Sy – стандартные отклонения этих переменных. Числитель в приведенной формуле включает в себя сумму попарных произведений, которая выражает взаимодействие двух переменных X и Y. Знаменатель в формуле введен для нормирования числителя таким образом, чтобы коэффициент корреляции стал безразмерным, и его можно было легко интерпретировать числом в диапазоне от –1 до +1. Еще раз подчеркнем, что коэффициент корреляции характеризует только линейную зависимость. Если абсолютная величина коэффициента корреляции равна 1, то это указывает на идеальную (функциональную) линейную взаимосвязь. Если коэффициент корреляции равен 0, то это означает, что между переменными отсутствует линейная зависимость. В таком случае требуется дополнительный анализ, поскольку переменные либо являются независимыми, либо взаимосвязь между ними имеет нелинейный характер. 