Бесконечнобольшие(б.б.) и бесконечномалые(б.м.) последовательности
{xn}- называется бесконечно большой, если для любого М>0, существует такой номер N, что для всех n с номерами n>N, выполняется условие, что |xn|>M. ("M>0$NM:"n>N=>|Xn|>M)
{xn}- называется бесконечно малой, если для любого М>0, существует такой номер N, что для всех n с номерами n>N, выполняется условие, что |xn|<M.
Теорема: если последовательность {xn}-бесконечно большая и все её члены отличны от нуля, то последовательность 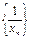 -бесконечно малая и обратно, если {an}-бесконечно малая, и члены отличны от нуля, то
-бесконечно малая и обратно, если {an}-бесконечно малая, и члены отличны от нуля, то 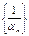 -бесконечно большая последовательность.
-бесконечно большая последовательность.
Доказательство:
Пусть {xn}-бесконечно большая. "M>0$NM:"n>N=>|Xn|>M. Пусть 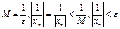 , "n>N – бесконечно малая и обратно.
, "n>N – бесконечно малая и обратно.
Основные свойства бесконечно малых/больших последовательностей.
Теорема: сумма и разность б.м.п. есть б.м.п. Док-во: an – б.м., bn-б.м. "e/2>0$N1:"n>N1=>|an|<e/2, "e/2>0$N2:"n>N2=>|bn|<e/2. N=max{N1,N2}, тогда "n>N будут одновременно выполнятся |an|<e/2 и |bn|<e/2 => "n>N |an+-bn| £ |an|+|bn| < e/2+e/2=e, "n>N |an+-bn| < e - бесконечно малая.
Следствие: алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть б.м.п.
Теорема: Произведение двух б.м.п. есть б.м.п.
Док-во: an – б.м., bn-б.м. Так как an – б.м., то "e>0$N1:"n>N1=>|an|<e, e=1$N2:"n>N2=>|bn|<1. N=max{N1,N2}, тогда "n>N существует |an|<e и |bn|<1 => |an|*|bn|<e*1=e, |an*bn|-бесконечно малая.
Следствие: произведение любого конечного числа б.м.п. есть б.м.п.
Замечание: частное 2-х б.м.п. может не быть б.м.п.
Последовательность {Xn} называется ограниченной, если существует такое c>0, что для всех членов последовательности выполняется: $c>0:"n>N=>|Xn|>c
Теорема: произведение ограниченной последовательности на б.м. есть б.м.п. Док-во: Пусть Xn-ограниченная, an – б.м. Так как Xn-ограниченная, то $c>0:"n>N=>|Xn|>c, так как an – б.м., то e/с>0$N:"n>N=>|an|<e/с. Тогда |Xn*an| = |Xn|*|an| < c*e/c=e, |Xn*an|<c-б.м.п.
Теорема: 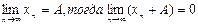
Замечание: 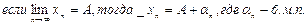
Предел функции.
Основные определения.
Пусть функция f(x) определена в некоторой окрестности х0, кроме может быть самой точки х0.
Определение 1(конечный предел в конечной точке): число А называют пределом функции f(x), при х®х0, если для любого e>0, существует дельта (d)>0, зависящая от e, такое что для всех произвольных х, принадлежащих d окрестности х0 и отличных от х0 удовлетворяющих неравенству, что |x-x0|<d выполняется, что |f(x)-A|<e. Т.е. 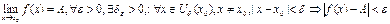 .
.
Определение 2 (конечный предел на бесконечности)
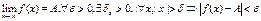
Определение 3 (бесконечный предел, в конечной точке)
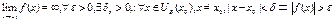
Определение 4 (бесконечный предел на бесконечности)
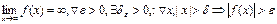
Определение 5 (на языке последовательности): число А(конечное/бесконечное) называется пределом функции f(x), х®х0(конечному/бесконечному), если для любой сходящейся к х0 последовательности значений аргумента х (х1,х2,..хn) отличных от х0) соответствующая последовательность f(x1),f(x2),..f(xn) значений функции сходится к числу А.
