Методические указания для выполнения контрольной работы
ПЕРЕЧЕНЬ ТЕМ САМОСТОЯТЕЛЬНОЙ РАБОТЫ.
Дисциплина: Элементы высшей математики
Специальность: 230115 Программирование в компьютерных системах
| № п/п | Содержание самостоятельной работы |
| 1. | Составление уравнения прямых. |
| 2. | Кривые 2 порядка: окружность, эллипс,гипербола,парабола. |
| 3. | Построение кривых 2 порядка. |
| 4. | Составление уравнений кривых 2-го порядка |
| 5. | Непрерывные функции, их свойства. Замечательные пределы. |
| 6. | Точки разрыва, их классификация. |
| 7. | Правило Лопиталя. |
| 8. | Вычисление односторонних пределов. |
| 9. | Монотонность функции. Экстремумы функций. |
| 10. | Асимптоты графика функции. |
| 11. | Выпуклость и вогнутость графика функции. Точки перегиба. |
| 12. | Исследование функции с помощью производной 1,2 порядков. |
| 13. | Неопределенный интеграл, его свойства, таблица основных интегралов. |
| 14. | Определённый интеграл, его свойства. |
| 15. | Вычисление площадей фигур с помощью определённого интеграла |
| 16. | Нахождение области определения функций двух переменных |
| 17. | Предел и непрерывность. Частные производные. |
| 18. | Частные производные высших порядков. |
| 19. | Двойные интегралы и их свойства. Повторные интегралы. |
| 20. | Определение обыкновенных ДУ. Общее и частное решение. Уравнения с разделёнными и разделяющимися переменными. |
| 21. | Однородные уравнения 1 -го порядка. Уравнения, приводящиеся к однородным. |
| 22. | Двойные интегралы и их свойства. Повторные интегралы. |
| 23. | Определение обыкновенных ДУ. Общее и частное решение. Уравнения с разделёнными и разделяющимися переменными. |
| 24. | Однородные уравнения 1 -го порядка. Уравнения, приводящиеся к однородным. |
| 25. | ДУ 1 -го порядка с разделяющимися переменными. Решение ОДУ 1-го порядка |
| 26. | Линейные однородные уравнения 2-го порядка с постоянными коэффициентами. |
| 27. | Линейные неоднородные уравнения 2-го порядка с постоянными коэффициентами. |
| 28. | ДУ, допускающие понижение степеней |
Литература.
1. Щипачев B.C. «Высшая математика». - М.. «Высшая школа», 2008;
2. Григорьев В.П., Дубинский Ю. А. «Элементы высшей математики», М- «Академия», 2008;
3. Богомолов Н. «Практические занятия по математике». - М.. «Высшая школа», 2008;
4. Пискунов Н.С. «Дифференциальное и интегральное исчисление». Т. 1,2. - М., «Наука», 2008;
5. Щипачев B.C. «Курс высшей математики», М-Проспект, 2009.
6. Кремер Н. Ш. «Высшая математика для экономических специальностей», ч. 1,2, М-2010г.
7. В. И. Ермакова «Сборник задач по высшей математике для экономистов», М- Инфра, 2010г.
Специальность: 230115 Программирование в компьютерных системах
Группа:ПКC-5208
Предмет: Элементы высшей математики
Преподаватель:Афонина надежда Евгеньевна
Правила выполнения и оформления
Контрольных работ
1. На титульном листе работы должны быть разборчиво написаны фамилия и инициалы студента, номер варианта (соответствует последней цифре в номере зачётной книжки)
2. Решения задач необходимо располагать в порядке номеров, указанных в задании, сохраняя номера задач.
3. Перед решением задачи следует выписать полностью ее условие.
4. Решение задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.
5. Если после проверки контрольной работы поставлена отметка "Неудовлетворительно", необходимо в этой же тетради сделать работу над ошибками и представить работу для повторной проверки. Это необходимо сделать в кратчайшие сроки.
Вариант №1.
1. Решите систему уравнений по формулам Крамера, методом обратной матрицы и методом Гаусса:
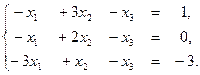
2. Даны вершины треугольника 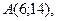
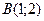 ,
, 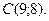
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 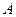 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 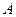 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 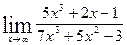 ; б)
; б) 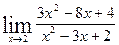 ; в)
; в) 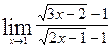 ;
;
г) 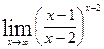 .
.
4. Найти производные заданных функций.
а) 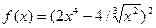 ; б)
; б) 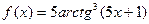 ;
;
5. Исследовать средствами дифференциального исчисления
функцию 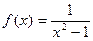 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 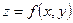 :
: 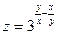 .
.
7.Найти общее решение дифференциального уравнения 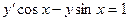
8. Найти неопределенные интегралы.
а) 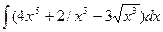 ; б)
; б) 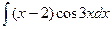 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 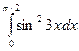 ; б)
; б) 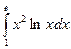
Вариант № 2.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
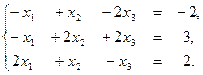
2. Даны вершины треугольника 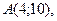
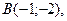 ,
, 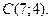
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 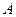 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 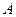 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 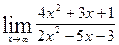 ; б)
; б) 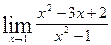 ; в)
; в) 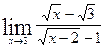 ;
;
г) 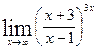 .
.
4. Найти производные заданных функций.
а) 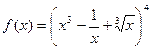 ; б)
; б) 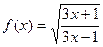 ;
;
5. Исследовать средствами дифференциального исчисления функцию 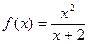 и построить ее график.
и построить ее график.
6. Найти общее решение дифференциального уравнения 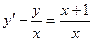 .
.
7. Найти частные производные и полный дифференциал функции 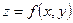 :
: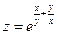 .
.
8. Найти неопределенные интегралы.
а) 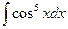 ; б)
; б) 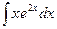 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 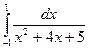 ; б)
; б) 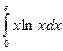 .
.
Вариант № 3.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
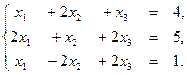
2. Даны вершины треугольника 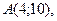
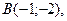 ,
, 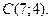
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 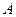 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 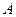 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 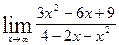 ; б)
; б) 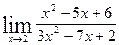 ; в)
; в) 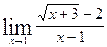 ;
;
г) 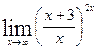 .
.
4. Найти производные заданных функций.
а) 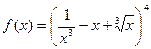 ;
;
б) 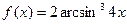 .
.
5. Исследовать средствами дифференциального исчисления функцию 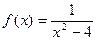 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 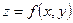 :
: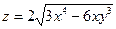
7. Найти общее решение дифференциального уравнения 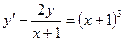 .
.
8. Найти неопределенные интегралы.
а) 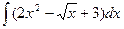 ; б)
; б) 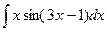 ;
;
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница. а) 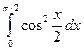 ; б)
; б) 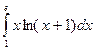
Вариант № 4.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
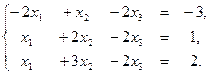
2. Даны вершины треугольника 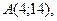
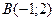 ,
, 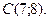
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 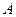 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 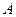 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 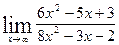 ; б)
; б) 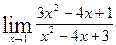 ; в)
; в) 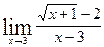 ;
;
г) 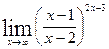 .
.
4. Найти производные заданных функций.
а) 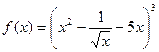 ; б)
; б) 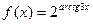 .
.
5. Исследовать средствами дифференциального исчисления функцию 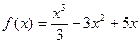 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 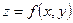 :
: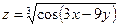
7. Найти общее решение дифференциального уравнения 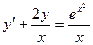 .
.
8. Найти неопределенные интегралы.
а) 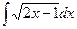 ; б)
; б) 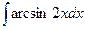 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 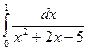 ; б)
; б) 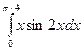
Вариант № 5.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
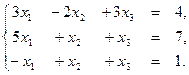
2. Даны вершины треугольника 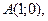
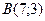 ,
, 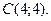
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 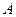 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 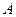 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 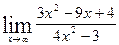 ; б)
; б) 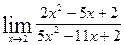 ; в)
; в) 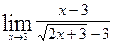 ;
;
г) 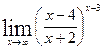 .
.
4. Найти производные заданных функций.
а) 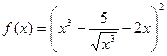 ; б)
; б) 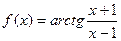
5. Исследовать средствами дифференциального исчисления функцию 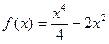 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 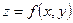 :
: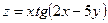
7. Найти общее решение дифференциального уравнения 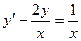 .
.
8. Найти неопределенные интегралы.
а) 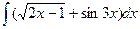 ; б)
; б) 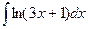 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 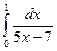 ; б)
; б) 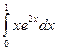 .
.
Вариант № 6.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
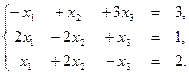
2. Даны вершины треугольника 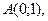
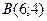 ,
, 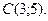
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 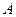 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 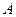 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 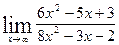 ; б)
; б) 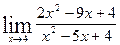 ;
;
в) 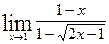 ; г)
; г) 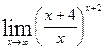 .
.
4. Найти производные заданных функций.
а) 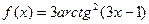 ;
;
б) 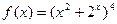 .
.
5. Исследовать средствами дифференциального исчисления функцию 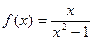 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 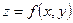 :
: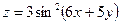
7. Найти общее решение дифференциального уравнения 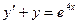 .
.
8. Найти неопределенные интегралы.
а) 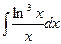 ; б)
; б) 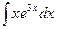 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 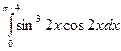 ; б)
; б) 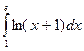 .
.
Вариант № 7.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
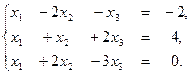
2. Даны вершины треугольника 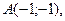
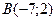 ,
, 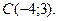
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 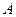 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 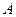 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 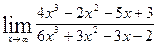 ; б)
; б) 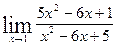 ; в)
; в) 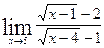 ;
;
г) 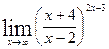 .
.
4. Найти производные заданных функций.
а) 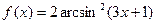 б)
б) 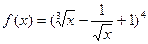 .
.
5. Исследовать средствами дифференциального исчисления функцию 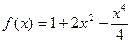 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 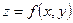 :
: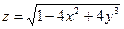
7.Найти общее решение дифференциального уравнения 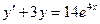 .
.
8. Найти неопределенные интегралы.
а) 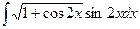 ; б)
; б) 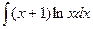 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 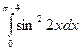 ; б)
; б) 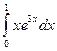 .
.
Вариант № 8.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
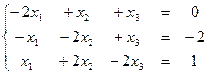
2. Даны вершины треугольника 
 ,
, 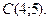
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 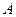 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 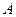 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 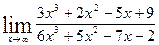 ; б)
; б) 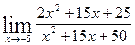 ; в)
; в) 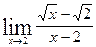 ;
;
г) 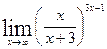 .
.
4. Найти производные заданных функций.
а) 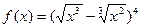 ;
;
б) 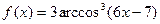 .
.
5. Исследовать средствами дифференциального исчисления функцию 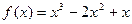 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции:
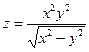
7. Найти общее решение дифференциального уравнения 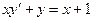 .
.
8. Найти неопределенные интегралы.
а) 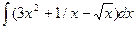 ; б)
; б) 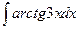 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 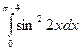 ; б)
; б) 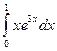 .
.
Вариант № 9.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
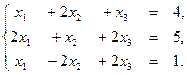
2. Даны вершины треугольника 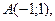
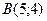 ,
, 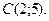
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 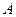 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 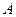 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 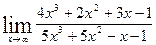 ; б)
; б) 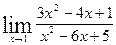 ; в)
; в) 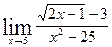 ;
;
г) 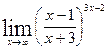 .
.
4. Найти производные заданных функций.
а) 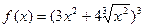 ;
;
б) 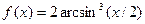 .
.
5. Исследовать средствами дифференциального исчисления функцию 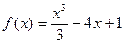 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции 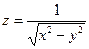 .
.
7.Найти общее решение дифференциального уравнения 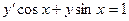 .
.
8. Найти неопределенные интегралы.
а) 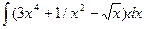 ; б)
; б) 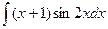 .
.
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 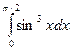 ; б)
; б) 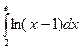
Вариант № 0.
1. Решите систему уравнений по формулам Крамера, с помощью обратной матрицы, методом Гаусса:
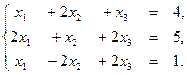
2. Даны вершины треугольника 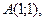
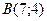 ,
, 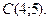
Найти: а) уравнения всех трех его сторон;
в) внутренний угол 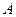 треугольника;
треугольника;
г) длину высоты, проведенной из вершины 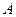 ;
;
д) площадь треугольника.
3. Найти пределы функций.
а) 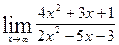 ; б)
; б) 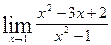 ; в)
; в) 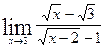 ;
;
г) 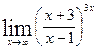 .
.
4. Найти производные заданных функций.
а) 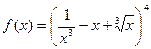 ; б)
; б) 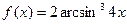 .
.
5. Исследовать средствами дифференциального исчисления функцию 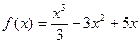 и построить ее график.
и построить ее график.
6. Найти частные производные и полный дифференциал функции
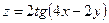 :
:
7. Найти общее решение дифференциального уравнения 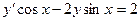 .
.
8. Найти неопределенные интегралы.
а) 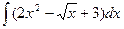 ; б)
; б) 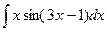 ;
;
9. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 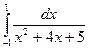 ; б)
; б) 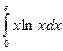 .
.
Методические указания для выполнения контрольной работы.
1.Решите систему 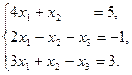 методом Крамера, методом обратной матрицы и методом Гаусса.
методом Крамера, методом обратной матрицы и методом Гаусса.
Решение.
Вычислим определитель матрицы 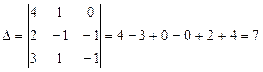 .
.
Так как определитель отличен от нуля, то система имеет единственное решение.
1) Метод Крамера: 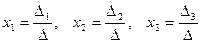 .
.
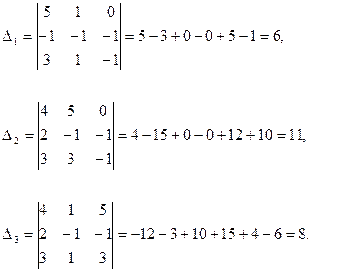
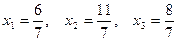 .
.
2) Метод обратной матрицы:
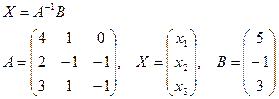
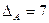
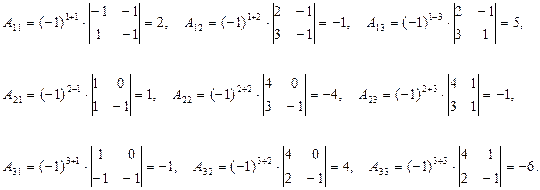
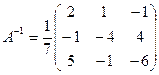
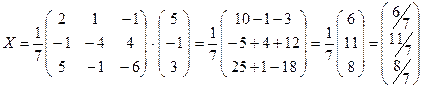
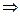
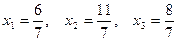 .
.
3) Метод Гаусса:
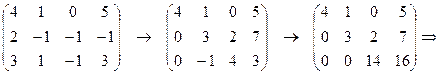
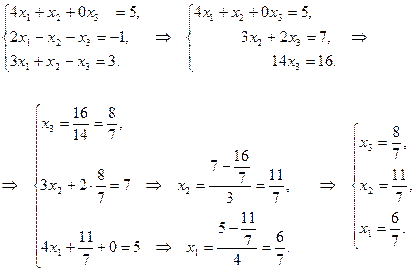
Вывод.Сравнивая результаты во всех трёх случаях, видим, что решения совпадают: 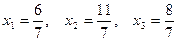 .
.
2. Даны вершины треугольника А(-3;-2), В(1;8), С(5;3).
Найти: а) уравнения всех трех его сторон;
в) внутренний угол А треугольника;
г) длину высоты, опущенной из вершины А;
д) площадь треугольника.
Решение.
а)Уравнения сторон найдем по формуле прямой, проходящей через две данные точки 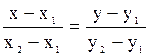
Уравнение стороны АВ: 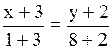 , или
, или 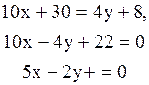 (АВ).
(АВ).
Уравнение стороны АС: 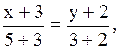 или
или 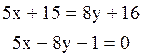 (АС)
(АС)
в)Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле 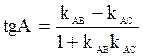 .
.
Угловые коэффициенты прямых выложим по формуле 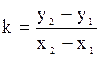 .
.
Получим 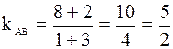 ;
; 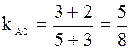 .
.
Тогда 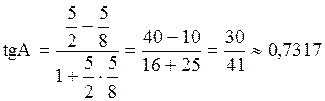
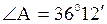 . Угол определяем с помощью таблицы тангенсов или калькулятора
. Угол определяем с помощью таблицы тангенсов или калькулятора
г)Длину высоты AD^BC найдем как расстояние от данной точки
А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле
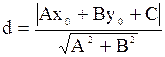 , где А, В, С – коэффициенты прямой,
, где А, В, С – коэффициенты прямой, 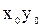 - координаты данной точки.
- координаты данной точки.
Получим 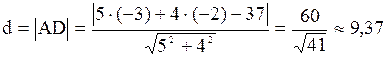 (мин. ед.)
(мин. ед.)
д)Площадь треугольника можно вычислить несколькими способами.
Вычислить ее через координаты вершин треугольника по формуле 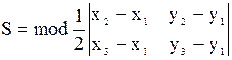 .
.
Получим 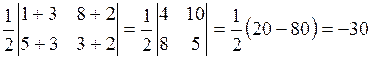 .
.
Итак, площадь треугольника SABC = 30 кв. ед.
3. Найти пределы функций.
а) 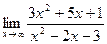 .
.
Здесь также непосредственно теорему о пределе дроби применить нельзя, так как числитель и знаменатель дроби при  не имеют конечных пределов. Это неопределенность вида
не имеют конечных пределов. Это неопределенность вида  . Для раскрытия ее разделим числитель и знаменатель на х в высшей степени, т.е. на
. Для раскрытия ее разделим числитель и знаменатель на х в высшей степени, т.е. на 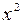 ,изатем перейдем к пределу.
,изатем перейдем к пределу.
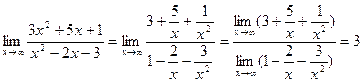 .
.
Здесь 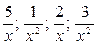 - бесконечно малые функции при
- бесконечно малые функции при 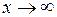 , и поэтомуих пределы равны нулю.
, и поэтомуих пределы равны нулю.
б) 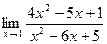 .
.
Имеем неопределенность вида 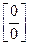 . Для раскрытия этой неопределенности преобразуем дробь, разложив числитель и знаменатель на множители. Для значения
. Для раскрытия этой неопределенности преобразуем дробь, разложив числитель и знаменатель на множители. Для значения 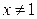 имеем тождество
имеем тождество
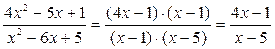 .
.
Поэтому пределы этих функций равны между собой:
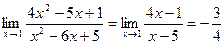 .
.
в) Найти 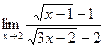 .
.
Непосредственная подстановка 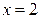 приводит к неопределенности вида
приводит к неопределенности вида  . Для того чтобы раскрыть эту неопределенность, выделим множитель
. Для того чтобы раскрыть эту неопределенность, выделим множитель 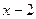 в числителе и в знаменателе. Для этого умножим числитель и знаменатель дроби на выражения, сопряженные, соответственно, числителю и знаменателю:
в числителе и в знаменателе. Для этого умножим числитель и знаменатель дроби на выражения, сопряженные, соответственно, числителю и знаменателю:
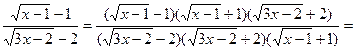
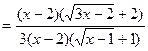 .
.
Тогда
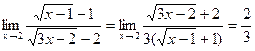 ..
..
4. 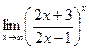 .
.
Здесь имеем неопределенность вида 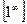 . Для раскрытия этой неопределенности преобразуем функцию так, чтобы можно было воспользоваться вторым замечательным пределом.
. Для раскрытия этой неопределенности преобразуем функцию так, чтобы можно было воспользоваться вторым замечательным пределом.
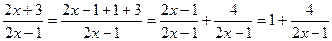 .
.
Введем новую переменную. Пусть 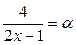 , тогда
, тогда 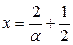 , при
, при 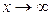 ,
, 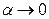 . Следовательно:
. Следовательно:
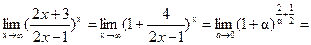
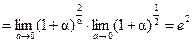 .
.
5. Найти производные заданных функций.
а) 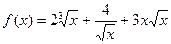 .
.
Преобразуем функцию: 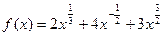 . Тогда
. Тогда
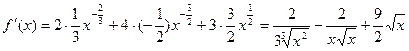 .
.
Б) 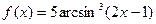
Находим производную сложной функции:
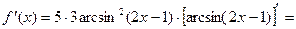
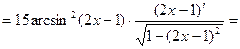
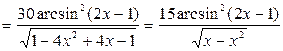 .
.
5. Исследовать средствами дифференциального исчисления функцию 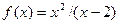 и построить ее график.
и построить ее график.
1) Функция определена при всех значениях х, кроме х=2, т.е.
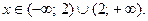
2) Четность. 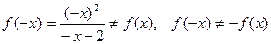 . Функция не является ни четной, ни нечетной.
. Функция не является ни четной, ни нечетной.
3) Функция не периодическая.
4) Найдем точки пересечения графика с осями координат.
Очевидно, если х=0, то у=0, и если у=0, то х=0. Следовательно, график функции проходит через начало координат.
5) Функция непрерывна в области своего определения.
Поскольку 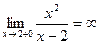 и
и 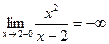 , то точка х=2является точкой разрыва второго рода. Исследуем поведение функции на бесконечности.
, то точка х=2является точкой разрыва второго рода. Исследуем поведение функции на бесконечности.
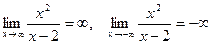 .
.
6) Найдем ассимптоты графика функции. Известно, что если 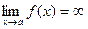 , то прямая
, то прямая 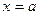 является вертикальной асимптотой графика функции. Если
является вертикальной асимптотой графика функции. Если 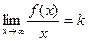 и
и 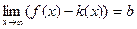 , то прямая
, то прямая 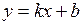 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 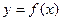 . Поскольку
. Поскольку 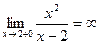 и
и 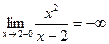 , то прямая х=2 является вертикальной асимптотой графика функции.
, то прямая х=2 является вертикальной асимптотой графика функции.
Найдем
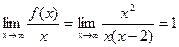 ; т.е. k=1.
; т.е. k=1.
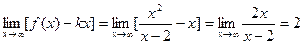 , т.е.
, т.е. 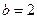 .
.
Следовательно, прямая 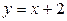 является наклонной асимптотой графика функции.
является наклонной асимптотой графика функции.
2. 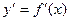 .
.
Найдем промежутки монотонности функции и точки экстремума. Для этого определим 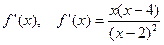 . Производная обращается в ноль при х=0 и 4, апри х=2 не существует.
. Производная обращается в ноль при х=0 и 4, апри х=2 не существует.

+ - - +
0 2 4 X
При 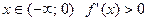 , следовательно, на этом интервале функция возрастает.
, следовательно, на этом интервале функция возрастает.
При 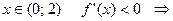 функция на этом интервале убывает. Следовательно, х=0является точкой максимума.
функция на этом интервале убывает. Следовательно, х=0является точкой максимума.
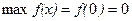 .
.
При 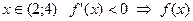 - убывает.
- убывает.
При 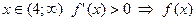 - возрастает.
- возрастает.
Следовательно, при х =4 функция имеет минимум:
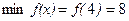 .
.
3. 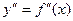 .
.
Определимпромежутки выпуклости и вогнутости графика функции. Для этого найдем вторую производную: 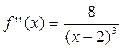 .
.
Вторая производная 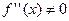 на области определения и не существует при х=2. Исследуем знак второй производной.
на области определения и не существует при х=2. Исследуем знак второй производной.

- +
Ç 2 È X
При 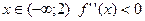 , следовательно, вэтом интервале график функции выпуклый.
, следовательно, вэтом интервале график функции выпуклый.
При 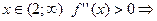 график функции вогнутый. Точек перегиба график функциине имеет.
график функции вогнутый. Точек перегиба график функциине имеет.
4. График: 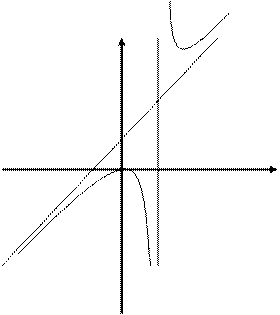
Y
-2 0 2 X
6. Найти частные производные и полный дифференциал функции : 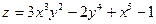
Решение
Найдём частные производные 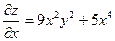 ;
; 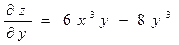 . Составим полный дифференциал по формуле
. Составим полный дифференциал по формуле 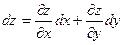 .
.
Получим 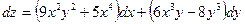 .
.
7.Найти общее решение дифференциального уравнения 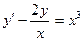 .
.
Решение.
Это уравнение первого порядка является линейным, так как это удовлетворяет общему виду линейных уравнений 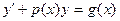 . Будем искать решение в виде
. Будем искать решение в виде 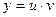 , где
, где 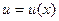 ,
, 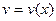 - дифференцируемые функции от
- дифференцируемые функции от 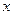 . Тогда
. Тогда 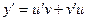 . Подставляя
. Подставляя 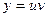 ,
, 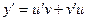 в данное уравнение, получим
в данное уравнение, получим
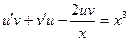
или 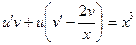 .
.