Геометрия на плоскости

Каноническое уравнение прямой на плоскости имеет вид

,

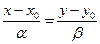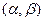где ¾ произвольная точка на прямой, а – направляющий вектор. Если уравнение прямой записано в виде

,

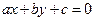то 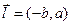– направляющий вектор, а 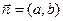- вектор нормали (направленный по перпендикуляру к прямой). Нам потребуется еще формула деления отрезка пополам: если задан отрезок 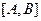, и координаты точек 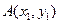, 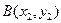известны, то серединой отрезка 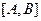является точка

.

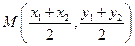Задача 1.3.В треугольнике ABC с вершиной A(10,7) известны уравнения высоты BB₁:

2x-y+37=0

и медианы CC₁:

8x+11y-162=0.

Написать уравнения всех сторон треугольника AB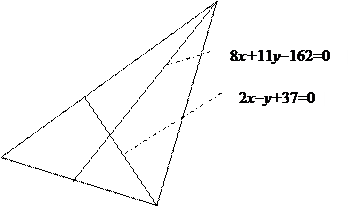C.

C

B₁

A(10,7)

C₁ B

Решение. Проще всего написать уравнение стороны , поскольку мы знаем точку , через которую проходит прямая , и знаем направляющий вектор (вектор нормали к высоте 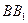). Следовательно, уравнение имеет вид

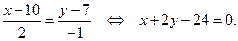
Чтобы написать уравнение прямой 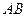, найдем сначала координаты точки 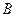. Обозначим эти координаты через 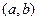. С одной стороны, точка лежит 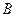на прямой 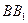, и, следовательно,

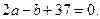
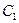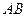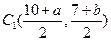С другой стороны, поскольку является серединой отрезка , то . Но 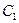лежит на прямой 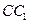, поэтому

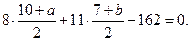
Решая совместно систему уравнений

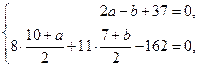
получаем

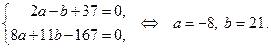
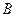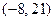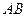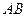Итак, точка имеет координаты , направляющий вектор прямой равен . Уравнение прямой имеет вид

Прежде чем написать уравнение прямой , найдем координаты точки 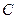. Она лежит на пересечении прямых и , поэтому ее координаты являются решением системы уравнений

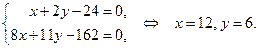
За направляющий вектор прямой можно взять вектор

,

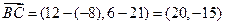а уравнение запишется в виде

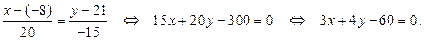Аналитическая геометрия в пространстве.

Нам необходимо знать следующие три операции над векторами в трехмерном пространстве.

1) Скалярное произведение векторов:

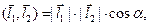
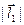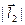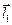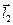где , – длины векторов и , а 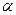- угол между ними. В координатах: если 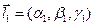, , то

2) Векторное произведение векторов: 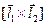есть вектор,

а) направленный по нормали к плоскости, натянутой на вектора , ;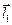

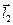б) имеющий длину, равную площади параллелограмма 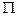, построенного на векторах , ;

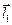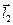в) и, наконец, направление вектора 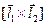должно быть таким, что вращение от вектора 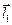к вектору 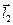внутри параллелограмма 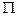будет осуществляться против часовой стрелки, если глядеть с конца стрелки вектора .

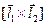В координатах:

.

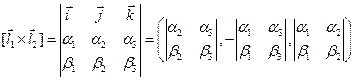3) Смешанное произведение векторов:

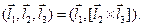
В координатах:

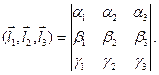
Геометрический смысл смешанного произведения векторов состоит в том, что 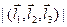есть объем параллелепипеда, построенного на векторах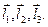

Каноническое уравнение прямой в пространстве имеет вид:

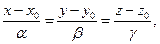
где 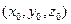- координаты произвольной точки прямой, а есть произвольный направляющий вектор.

Имеется два типа уравнения плоскости в пространстве

а) .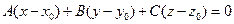

Здесь 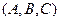- вектор нормали к плоскости, а 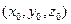- координаты произвольной точки плоскости.

б) ,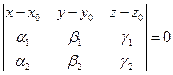

где 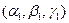, 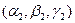- любые два неколлинеарных вектора, параллельных плоскости, а 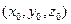, по-прежнему, произвольная точка плоскости.

Задача 1.4. В пирамиде ABCD с вершинами A(10,7,1), B(7,10,0), C(1,10,7), D(7,1,17) найти:

а) угол между ребрами AB и AD;

б) угол между ребром AD и плоскостью ABC;

в) площадь основания ABC;

г) объем пирамиды;

д) расстояние от вершины D до плоскости ABC.

Написать уравнение высоты, опущенной из вершины D на плоскость ABC, и уравнение плоскости ABC.

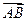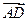Решение.а). Найдем векторы и в координатах. Напомним, что для этого следует из координат конца вектора вычесть координаты начала:

,

.

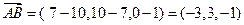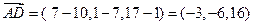Чтобы найти угол между векторами 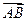, , 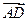вычислим скалярное произведение векторов 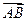и 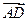в координатах, затем найдем длины векторов 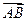и 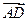, и подставим полученные значения в формулу скалярного произведения. Получаем:

,

,

.

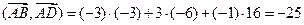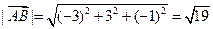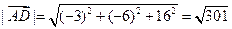Подставляем в формулу скалярного произведения:

,

откуда , .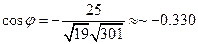

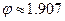б) Угол между ребром AD и плоскостью ABC равен 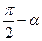, где 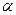- угол между ребром AD и нормалью к плоскости ABC. Начнем поэтому с вычисления нормали к плоскости ABC. В качестве вектора нормали можно взять векторное произведение векторов 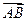и 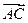(поскольку 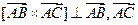). Вектор 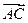в координатах имеет вид

.

Следовательно,

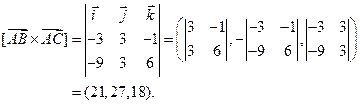
Обозначим для краткости 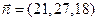. Теперь, как и в пункте а) вычислим скалярное произведение векторов 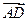и 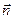, и с его помощью определим угол между векторами 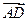и .

,

,

,

.

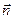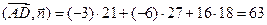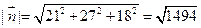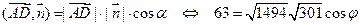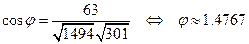Следовательно, угол между ребром AD и плоскостью ABC равен .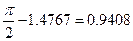

в) Площадь основания ABC равна половине площади параллелограмма, построенного на векторах 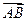и 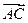. По второму свойству векторного произведения, длина вектора 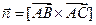как раз и равна площади этого параллелограмма. Следовательно,

.

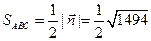г) Объем пирамиды равен одной шестой от объема параллелепипеда, построенного на векторах 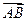, , 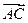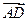. Объем параллелепипеда можно вычислить как модуль смешанного произведения . Имеем:

.

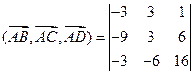Заметим, однако, что нам нет необходимости заново вычислять этот определитель, поскольку он равен скалярному произведению векторов 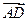и 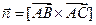, а эта величина была найдена выше, в пункте б). Следовательно,

.

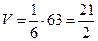д) Расстояние от вершины D до плоскости ABС можно найти, используя формулу объема пирамиды

,

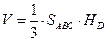поскольку все величины в ней, кроме высоты 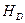(которая и равна расстоянию от точки D до плоскости ABС), уже известны. Получаем:

.

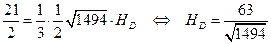В заключение, напишем уравнение высоты, опущенной из вершины D на плоскость ABC, и уравнение плоскости ABC.

Направляющий вектор высоты 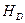равен 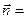(21,27, 18). Высота 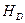проходит через точку D(7, -1,17). Следовательно, каноническое уравнение высоты имеет вид

.

Чтобы написать уравнение плоскости 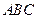, воспользуемся уравнением 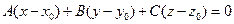. В качестве вектора 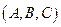вновь можно использовать вектор нормали 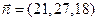, а в качестве 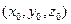– точку A(10,7,1). Получаем:

Задача полностью решена.

Предел и производная.