Примерный перечень вопросов к зачету и экзамену

Перечень вопросов к зачету

1. Корень n-ой степени и его свойства.

2. Степень с рациональным и действительным показателем и его свойства.

3. Степенная функция, ее свойства.

4. Иррациональные уравнения.

5. Показательная функция и ее свойства.

6. Показательные уравнения.

7. Логарифмы. Десятичные и натуральные Логарифмы.

8. Свойства логарифмов.

9. Логарифмическая функция.

10. Логарифмические уравнения.

11. Радианная мера угла.

12. Определение синуса, косинуса, тангенса и котангенса угла.

13. Зависимость между синусом, косинусом, тангенсом и котанген-сом одного и того же угла.

14. Тригонометрические тождества.

15. Синус, косинус, тангенс и котангенс углов α и –α.

16. Формулы сложения.

17. Синус, косинус, тангенс и котангенс двойного угла.

18. Синус, косинус, тангенс и котангенс половинного угла.

19. Формулы приведения.

20. Сумма и разность синусов. Сумма и разность косинусов.

Перечень вопросов к экзамену

1. Уравнение sinx=a.

2. Уравнение cosx=a.

3. Уравнение tgx=a и ctgx=a.

4. Решение тригонометрических уравнений.

5. Свойства функции у=sinx и ее свойства.

6. Свойства функции у=cosx и ее свойства.

7. Свойства функций у=tgx и у=ctgx, их свойства.

8. Производная.

9. Правила дифференцирования.

10. Производные некоторых элементарных функций.

11. Физический и геометрический смысл производной.

12. Возрастание и убывание функции.

13. Экстремумы функции.

14. Первообразная. Основное свойство первообразной. Неопределен-ный интеграл.

15. Вычисление интегралов.

16. Основные свойства пространства.

17. Отношения прямой и плоскости пространства.

18. Понятие многогранника.

19. Понятие тела вращения.

Перечень примерных контрольных вопросов и заданий для самостоятельной работы

1. Натуральные, целые, рациональные, иррациональные и действи-тельные числа.

2. Взаимно обратные функции.

3. Равносильные уравнения и неравенства.

4. Показательные неравенства.

5. Логарифмические неравенства.

6. Простейшие тригонометрические неравенства.

7. Обратные тригонометрические функции.

8. Наибольшее и наименьшее значение функции на отрезке.

9. Выпуклости функции и точки перегибов.

10. Методы вычисления неопределенных интегралов.

Перечень тестовых заданий

Тест №1

Вариант 1

1. Решить уравнение .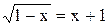

а) 1

б) 3

в) 8

г) 0

2. Найти корни уравнения .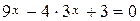

а) 0;2

б) 0;1

в) 0;3

г) 0;4

3. Решить неравенство .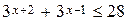

а) х 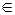(–∞;1)

б) х 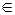(–∞;2]

в) х 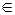(–∞;1]

г) х 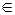(–∞;2)

4. Решить уравнение log₂(x–5)+log₂(x+2)=3.

а) 6

б) 4

в) 1

г) 9

5. Вычислить sin73⁰cos17⁰+cos73⁰sin17⁰.

а) 0

б)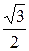

в) 1

г)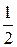

6. Вычислить cos²15⁰–sin²15⁰.

а)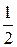

б) 0

в)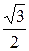

г) 1

Вариант 2

1. Решить уравнение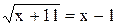

а) 9

б) 6

в) 4

г) 5

2. Найти корни уравнения .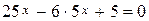

а) 0;2

б) 0;1

в) 3;4

г) 6;7

3. Решить неравенство .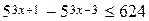

а) х 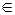(–∞;2]

б) х 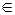(–∞;1]

в) х 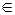(–∞;1)

г) х 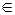(–∞;2)

4. Решить уравнение log₃(x–2)+log₃(x+6)=2.

а) 0

б) 3

в) 1

г) 4

5. Вычислить sin73⁰cos13⁰–cos73⁰sin13⁰.

а)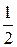

б)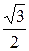

в) 1

г) 0

6. Вычислить 2sin15⁰·cos15⁰.

а)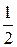

б) 1

в) 0

г)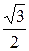

Тест №2

Вариант 1

1. Вычислить производную функции у=15lnх:

а) 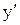=15х

б) =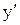

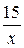
в) 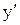=15ln²х

г) 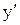=15х²

2. Найти наибольшее и наименьшее значение функции у=2х+1 на отрез-ке [0;2]:

а) f_mim=1, f_max=5

б) f_mim=2, f_max=10

в) f_mim=0, f_max=1

г) f_mim=1, f_max=2

3. Определить участки возрастания и убывания функции у= –2х³+1:

а) х 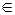(–∞;–2) – убывает, х 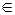(–2;+∞) – возрастает

б) х 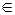(–∞;+∞) – убывает

в) х 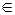(–∞;1) – убывает, х 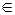(1;+∞) – возрастает

г) х 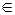(–∞;+∞) – возрастает

4. Вычислить интеграл :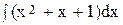

а)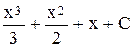

б) х³+х²+х+С

в) 2х+1+C

г)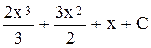

5. Вычислить интеграл :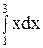

а) 5

б) 4

в) 6

г) 1

6. Найти площадь криволинейной трапеции, заключенной между лини-ями у=0, у=2х, х=1, х=2:

а) 5

б) 3

в) 6

г) 1

Вариант 2

1. Вычислить производную функции у=8arctg(х+8):

а) =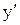

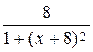
б) =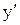

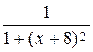
в) =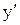

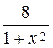
г) =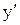

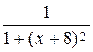
2. Составить уравнение касательной к функции у=3х+1 в точке х₀=0:

а) у_кас.=х

б) у_кас.=3х+1

в) у_кас.=3х–1

г) у_кас.=3х

3. Определить участки возрастания и убывания функции у= –3х³+1:

а) х 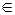(–∞;–3) – убывает, х 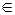(–3;+∞) – возрастает

б) х 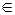(–∞;+∞) – убывает

в) х 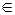(–∞;1) – убывает, х 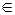(1;+∞) – возрастает

г) х 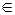(–∞;+∞) – возрастает

4. Вычислить интеграл :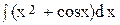

а)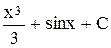

б) х²+sinx+С

в) 2х+sinx+C

г)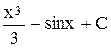

5. Вычислить интеграл :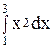

а)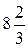

б)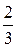

в)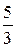

г)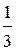

6. Найти площадь криволинейной трапеции, заключенной между лини-ями у=0, у=3х, х=1, х=2:

а)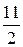

б)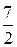

в)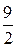

г)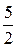

Литература

Рекомендуемая литература (основная).

1. Алгебра и начала анализа: Учеб. дл 10-11 кл. общеобразоват. Уч-реждений/Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 11 изд. – М.: Просвещение, 2003. – 384 с.

2. Шарыгин И.Ф. Геометрия. 10-11 кл.: Учеб. для общеобразоват. учеб. заведений. – М.: Дрофа, 1999. – 208 с.

Рекомендуемая литература (дополнительная).

1. Алгебра и начала анализа: учебник для 10-11 классов общеобразо-вательных учреждений/Под ред. А.Н. Колмогорова. – 16-е изд. Москва: Просвещение, 2007. – 383 с.

2. Алгебра и начала анализа. 10 класс.: учеб. для общеобразователь-ных учреждений/Ю.М. Колягин. – 6-е изд. Москва: Мнемозина, 2007. – 363 с.

3. Домашняя работа по алгебре за 10 класс.: к учебнику «Алгебра и начала анализа: учебник для 10-11 кл. общеобразовательных учреждений/Ш.А. Шалимов и др. – 13-е изд. М.: Просвещение, 2005»: учеб. метод. пособие/Лаппо Л.Д., Морозов А.В. М.: Экзамен, 2007 (Владимир: Владимирская книжная типография. – 223 с. – Решебник).

4. Геометрия. 10 класс.: учебник для классов с углубленным и про-фильным изучением математики/Е.В. Потоскуев, Л.И. Звавич; под науч. ред. А.Р. Рязановского. – 5-е изд., стер. Москва: Дрофа, 2007. – 223 с.

5. Геометрия. 10-11.: учебник для общеобразовательных учрежде-ний: базовый и профильный уровни/Л.С. Атанасян и др. – 16-е изд. Москва: Просвещение, 2007: Московские учеб. – 255 с.

6. Все домашние работы за 10 класс.: учеб.-метод. пособие/Ивашова О.Д. и др. М.: Экзамен, 2006: ГУП ИПК Ульян. Дом печати – 735 с.