Обыкновенные дифференциальные уравнения

Задание
1. Решить дифференциальное уравнение , , ,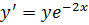
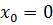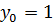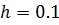, на отрезке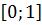

· аналитическим методом (решение )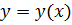

· методом Эйлера с шагом ( ) .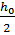

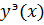· методом Рунге-Кутта 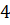-го порядка (программно)

2. Вычислить погрешность для ,

, , .

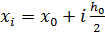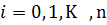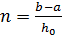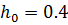3. Вычислить погрешность , .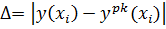
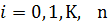4. Дать графическую иллюстрацию решений.

Исследование задания
Аналитический способ решения данного уравнения – метод разделения переменных.
Запишем уравнение в виде 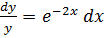и проинтегрируем с учётом начальных условий.

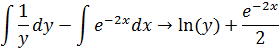
Получаем 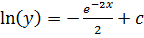, 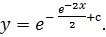Из начальных условий следует 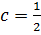, следовательно, аналитическое решение ОДУ имеет вид .

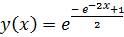Решение уравнения методом Эйлера: , .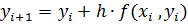

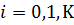Для интегрирования дифференциального уравнения методом Рунге-Кутта 4-го порядка воспользуемся формулами:
, .
,

,

,

.

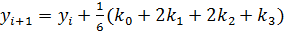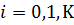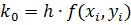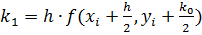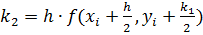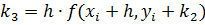Воспользуемся программными средствами для решения уравнения методом Эйлера.

Скриншот работы программы

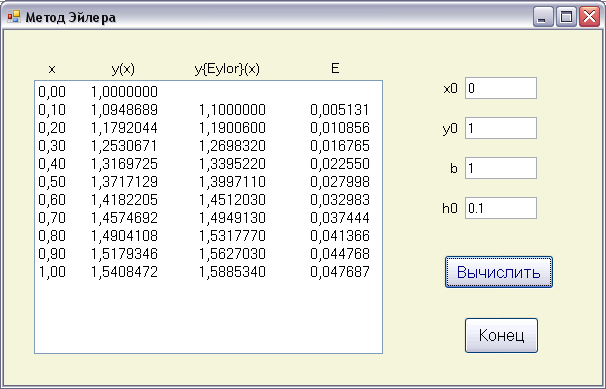
Исходный код программы

Imports System.Math Public Class Form1   Function f(ByVal x As Single, ByVal y As Single) f = y * Exp(-2 * x) End Function Function F_toch(ByVal x As Single) Return Exp((1 / 2) - ((Exp(-2 * x)) / (2))) End Function Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function Sub vivod(ByVal x As Single, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub vivodint(ByVal x As Integer, ByVal T As TextBox) T.Text = CStr(x) End Sub     Sub difur(ByVal x0 As Single, ByVal y0 As Single, ByVal b As Single, _ ByVal h0 As Single, ByRef L As ListBox) Dim h, y, ep As Single, z, z1, z2 As String Dim i, n As Integer n = (b - x0) / h0 z1 = Format(F_toch(x0), "0.0000000") + Space(3) z2 = Format(y, "0.000000") + Space(4) z = Format(x0, "0.00") + Space(6) + z1 L.Items.Add(z) For i = 1 To n h = h0 y = rung((x0), (y0), h)   x0 = x0 + h0 y0 = y ep = Abs(F_toch(x0) - y) If F_toch(x0) > 100 Then z1 = Format(F_toch(x0), "0.0000000") + Space(3) ElseIf F_toch(x0) >= 10 Then z1 = Format(F_toch(x0), "0.0000000") + Space(5) Else z1 = Format(F_toch(x0), "0.0000000") + Space(7) End If If y > 100 Then z2 = Format(y, "0.0000000") + Space(4) ElseIf y >= 10 Then z2 = Format(y, "0.0000000") + Space(6) Else z2 = Format(y, "0.0000000") + Space(8) End If z = Format(x0, "0.00") + Space(6) + z1 + Space(3) + z2 + Space(3) + Format(ep, "0.000000") L.Items.Add(z) Next End Sub Function rung(ByVal x As Single, ByVal y As Single, ByVal h As Single) Dim k1 As Single k1 = f(x, y)   y = y + h * k1 x = x + h   rung = y End Function Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim y0, b, x0, h0 As Single   x0 = vvod(TextBox1) y0 = vvod(TextBox2) b = vvod(TextBox3)   h0 = vvod(TextBox4) difur(x0, y0, b, h0, ListBox1) End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub End Class

Воспользуемся программными средствами для решения уравнения методом Рунге-Кутта 4-го порядка.

Скриншот работы программы

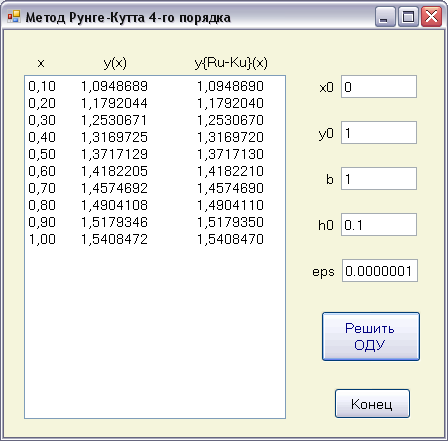
Исходный код программы

Imports System.Math Public Class Form1   Function f(ByVal x As Single, ByVal y As Single) f = y * Exp(-2 * x) End Function   Function F_toch(ByVal x As Single) Return Exp((1 / 2) - ((Exp(-2 * x)) / (2))) End Function Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function Sub vivod(ByVal x As Single, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub vivodint(ByVal x As Integer, ByVal T As TextBox) T.Text = CStr(x) End Sub Function rung(ByVal x As Single, ByVal y As Single, ByVal h As Single, ByVal m As Integer) Dim k1, k2, k3, k4 As Single Dim j As Integer For j = 1 To m k1 = f(x, y) k2 = f(x + h / 2, y + h * k1 / 2) k3 = f(x + h / 2, y + h * k2 / 2) k4 = f(x + h, y + h * k3) y = y + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6 x = x + h Next j rung = y End Function Sub difur(ByVal x0 As Single, ByVal y0 As Single, ByVal b As Single, ByVal eps As Single, _ ByVal h0 As Single, ByRef L As ListBox) Dim h, x, y, y1 As Single, z, z1, z2 As String Dim i, m, n As Integer n = (b - x0) / h0   For i = 1 To n h = h0 m = 1 y = rung((x0), (y0), (h), (m)) Do y1 = y : h = h / 2 x = x0 : y = y0 : m = 2 * m y = rung((x), (y), (h), (m)) Loop Until Abs(y - y1) < eps x0 = x0 + h0 y0 = y   If F_toch(x0) > 100 Then z1 = Format(F_toch(x0), "0.0000000") + Space(3) ElseIf F_toch(x0) >= 10 Then z1 = Format(F_toch(x0), "0.0000000") + Space(5) Else z1 = Format(F_toch(x0), "0.0000000") + Space(7) End If If y > 100 Then z2 = Format(y, "0.0000000") + Space(4) ElseIf y >= 10 Then z2 = Format(y, "0.0000000") + Space(6) Else z2 = Format(y, "0.0000000") + Space(8) End If z = Format(x0, "0.00") + Space(6) + z1 + Space(5) + z2 + Space(3) L.Items.Add(z) Next End Sub Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim y0, b, x0, eps, h0 As Single   x0 = vvod(TextBox1) y0 = vvod(TextBox4) b = vvod(TextBox2) eps = vvod(TextBox3) h0 = vvod(TextBox5) difur(x0, y0, b, eps, h0, ListBox1) End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub End Class

Таблица решений уравнения

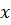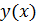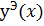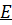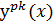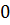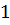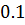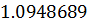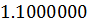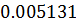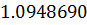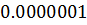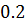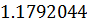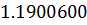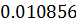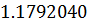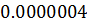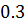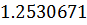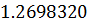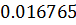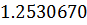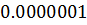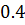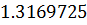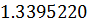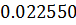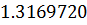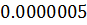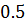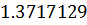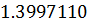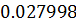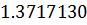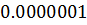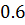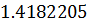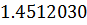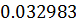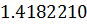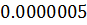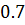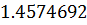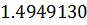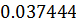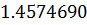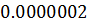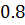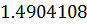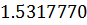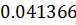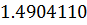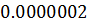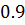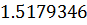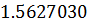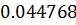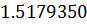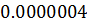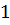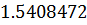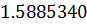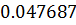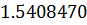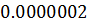Графические иллюстрации решений

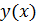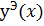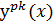6. АЛГОРИТМЫ РЕШЕНИЯ ЗАДАЧИ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Задание
1.Решить задачу оптимизации функции 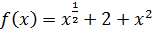c точностью 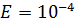методом золотого сечения.
2. Вычислить число итераций, необходимых, чтобы локализовать точку минимума с точностью .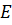
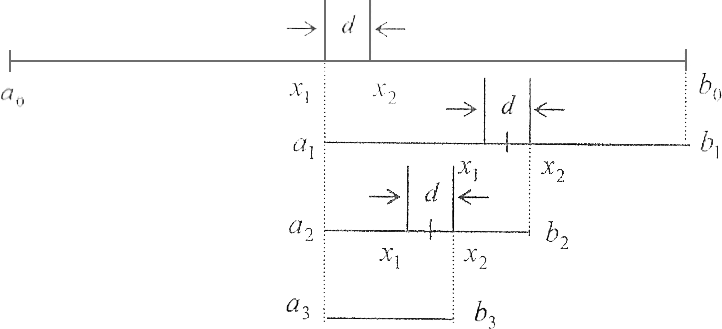
3. Методом дихотомии решить задачу оптимизации (три итерации).
4. Определить длину конечного отрезка, содержащего точку минимума.
5. Вычислить теоретическую точность оптимизации. Сравнить с результатом, полученным в п. 4.
6. Проиллюстрировать графическое решение задачи.

Исследование задания

График функции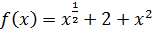

1) Определим отрезок унимодальности функции 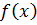. Практический критерий унимодальности функции требует непрерывности функции и выполнение условия 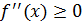при 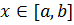или неубывания .
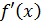Вторая производная 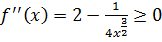при 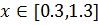, т.е. функция 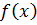- унимодальная на отрезке .

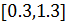Отрезок 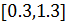- начальный отрезок неопределённости.

2) Теоретическая величина погрешности определяется соотношениями:
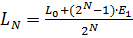– длина конечного отрезка после 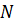итераций для метода дихотомии, 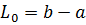- длина начального отрезка.

Для метода золотого сечения длина конечного отрезка после 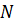итераций
.

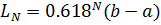Полагаем, что длина конечного отрезка неопределённости – мера погрешности.
3) Воспользуемся программными средствами для решения задачи оптимизации методом золотого сечения.

Скриншот работы программы

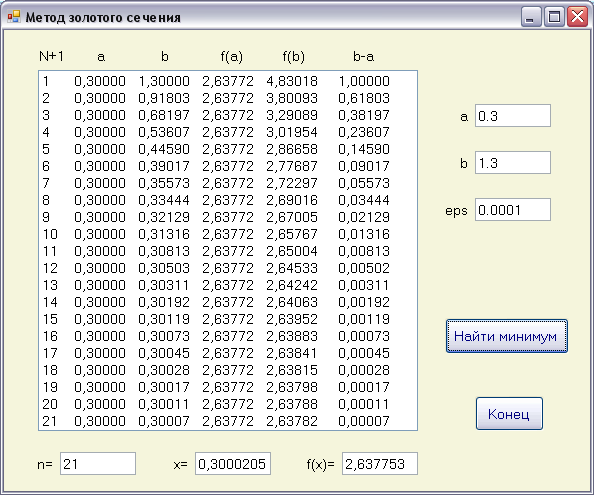
Исходный код программы

Imports System.Math Public Class Form1 Function f(ByVal x As Single) f = Sqrt(x) + 2 + x ^ 2 End Function   Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function Sub vivod(ByVal x As Single, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub vivodint(ByVal x As Integer, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub gold(ByVal a As Single, ByVal b As Single, ByVal eps As Single, _ ByRef x As Single, ByRef n As Integer, ByRef L As ListBox) Dim k1, k2, x1, x2, f1, f2 As Single, z As String k1 = (3 - Sqrt(5)) / 2 k2 = (Sqrt(5) - 1) / 2 x1 = a + k1 * (b - a) x2 = a + k2 * (b - a) f1 = f(x1) f2 = f(x2) n = 0 Do Until (b - a) < eps / 2 n = n + 1 If n > 100 Then z = CStr(n) + Space(2) ElseIf n >= 10 Then z = CStr(n) + Space(4) Else z = CStr(n) + Space(6) End If z = z + Format(a, "0.00000") + Space(3) + Format(b, "0.00000") + Space(3) + Format(f(a), "0.00000") + Space(3) z = z + Format(f(b), "0.00000") + Space(5) + Format(b - a, "0.00000") L.Items.Add(z) If f1 < f2 Then b = x2 : x2 = x1 x1 = a + k1 * (b - a) f2 = f1 : f1 = f(x1) Else a = x1 : x1 = x2 : f1 = f2 x2 = a + k2 * (b - a) f2 = f(x2) End If Loop x = (a + b) / 2 End Sub Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim a, b, x, eps As Single Dim n As Integer a = vvod(TextBox1) b = vvod(TextBox2) eps = vvod(TextBox3) gold(a, b, eps, x, n, ListBox1) vivodint(n, TextBox4) vivod(x, TextBox5) vivod(f(x), TextBox6)   End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub   End Class

, .

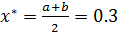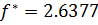Определим число итераций 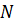, необходимых для локализации точки минимума с точностью 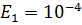из условия, что длина конечного отрезка неопределённости не превышает заданной точности.

.
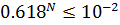𝑁≥ , .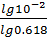

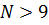При 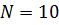длина конечного отрезка равна .
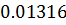Точность достигнута при 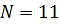, т.е. расчёт примерно совпадает с теоретической оценкой.

4) Воспользуемся программными средствами для решения задачи оптимизации методом дихотомии.

Скриншот работы программы

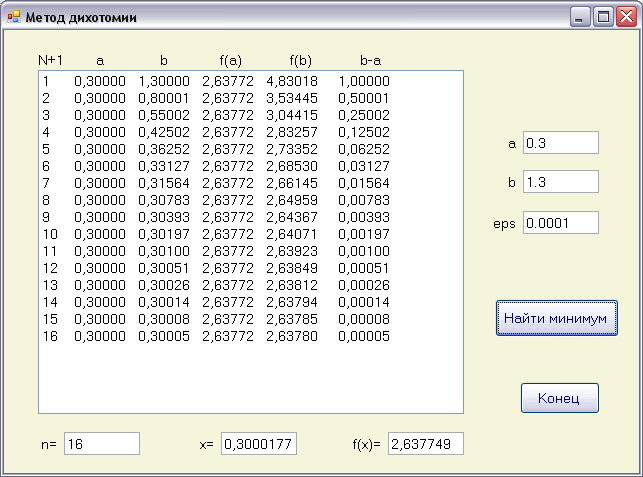
Исходный код программы

Imports System.Math Public Class Form1 Function f(ByVal x As Single) f = Sqrt(x) + 2 + x ^ 2 End Function   Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function Sub vivod(ByVal x As Single, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub vivodint(ByVal x As Integer, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub dihot(ByVal a As Single, ByVal b As Single, ByVal eps As Single, _ ByRef x As Single, ByRef n As Integer, ByRef L As ListBox) Dim d, x1, x2, f1, f2 As Single, z As String d = eps / 10 n = 0 Do x1 = (a + b) / 2 - d x2 = (a + b) / 2 + d f1 = f(x1) f2 = f(x2) n = n + 1 If n > 100 Then z = CStr(n) + Space(2) ElseIf n >= 10 Then z = CStr(n) + Space(4) Else z = CStr(n) + Space(6) End If z = z + Format(a, "0.00000") + Space(3) + Format(b, "0.00000") + Space(3) + Format(f(a), "0.00000") + Space(3) z = z + Format(f(b), "0.00000") + Space(5) + Format(b - a, "0.00000") L.Items.Add(z) If f1 > f2 Then a = x1 Else b = x2 End If Loop Until (b - a) < eps / 2 x = (a + b) / 2 End Sub Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim a, b, x, eps As Single Dim n As Integer a = vvod(TextBox1) b = vvod(TextBox2) eps = vvod(TextBox3) dihot(a, b, eps, x, n, ListBox1) vivodint(n, TextBox4) vivod(x, TextBox5) vivod(f(x), TextBox6)   End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub End Class

При 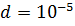определим длину конечного отрезка неопределённости и сравним с расчётом.
. .

.

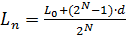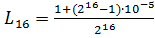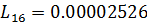Расчётная длина . .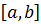
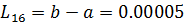Как мы видим, теоретическая точность оптимизации почти в 2 раза больше расчётной точности.

Графическая иллюстрация процесса оптимизации.