Задания для контрольных работ

Контрольные работы

По каждой части курса математики студент должен выполнить две контрольные работы, составленные из задач, приведенных в пособии:

МАТЕМАТИКА

Программы и контрольные задания для студентов 1 курса

экономических специальностей ФВЗО

М.Ю. Ястребов, СПб, СПбГУВК, 2001.

)

	Контрольная работа	№ задач по пособию
Часть 1	№ 1 № 2	1; 21; 31,2,3 ; 41,2 6а,б; 8; 9б
Часть 2	№ 1 № 2	11; 13; 14а,б 15; 16; 17

При выполнении контрольной работы студент из каждой задачи выбирает задание только своего варианта. Номер варианта легко определить по таблице:

Первая буква фамилии студента	А, Б	В, Г	Д, Е, Ж, З	И, К	Л, М	Н, О	П, Р	С, Т, У	Ф, Х, Ц, Ч, Ш, Щ	Э, Ю, Я
№ варианта

Без предъявления преподавателю контрольных работ студент не допускается к сдаче зачета или экзамена.

Контрольная работа выполняется в обычной (тонкой) школьной тетради, на обложку которой наклеивается титульный лист, с указанием Ф И О студента, курса, специальности, номера зачетной книжки (см. ниже отобранные задания из указанного пособия и образец оформления титульного листа).

Умение решать задачи по темам программы проверяется при проведении теста и является составной частью экзамена.

При решении тестового задания можно пользоваться своей контрольной работой.

Большую помощь при выполнении контрольных работ по 1 части могут оказать пособия, в которых подробно решены типовые задачи:

Математика. Часть 1 Методические указания к решению контрольной работы № 1для студентов 1 курса экономических специальностей ВЗО. М.Ю. Ястребов, СПбГУВК, 2002.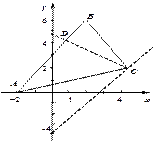
Математика. Часть 1 Методические указания к решению контрольной работы № 2для студентов 1 курса экономических специальностей ВЗО. М.Ю. Ястребов СПбГУВК, 2000.

Большую помощь при выполнении контрольных работ по 2 части могут оказать пособия:

Е.М. Пастушок Математика. Часть 2 Методические указания к решению контрольной работы № 1для студентов 1 курса экономических специальностей ВЗО СПбГУВК, 2002.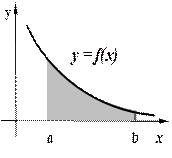

А.С. Кобелева Математика. Часть 2 Методические указания к решению контрольной работы № 2 для студентов 1 курса экономических специальностей ФВЗО. СПбГУВК, 2011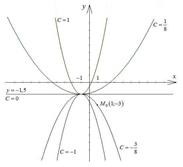

Студент может обращаться к преподавателю для получения письменной или устной консультации. Указания студенту по текущей работе даются также в процессе рецензирования контрольной работы.

Для студентов ФВЗО проводятся

еженедельные консультациипо математике.

Расписание консультаций находится на стендах деканата и на стенде кафедры математики.

Задания для контрольных работ

ЧАСТЬ 1. Контрольная работа № 1.

Задача 1. Выполнить матричные операции:

1. A×B+2×C, где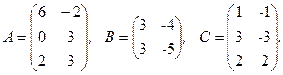

2. A-3×B×C, где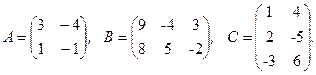

3. (2×A+3×B)×C, где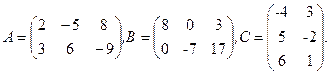

4. A×2×(B-2×C), где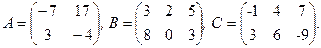

5. A×B-2×C×B, где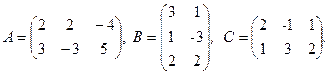

6. 2×A-B×C, где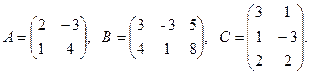

7. 3×A×B-2×C, где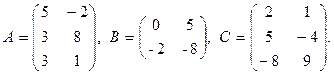

8. 4A×(2B+C), где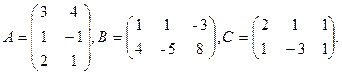

9. A×B+3×C×B, где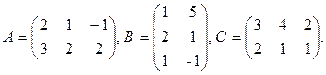

10. A×(2B-3C), где .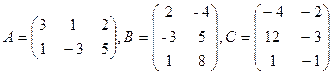

Задача 2. Решить системы линейных уравнений методами:

1) Крамера, 2) Гаусса, 3) матричным методом. Сделать проверку.

1.		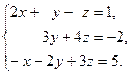6.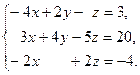
2.		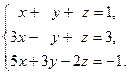7.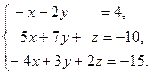
3.		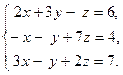8.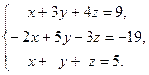
4.		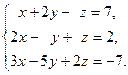9.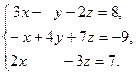
5.		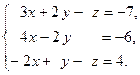10.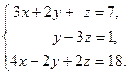

Задача 3. Даны координаты вершин пирамиды ABCD. Требуется:

1) записать векторы 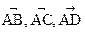в ортонормированном базисе 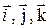; найти модули этих векторов;

2) вычислить скалярное произведение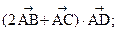

3) вычислить векторное произведение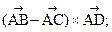

№ вар.	Координаты вершин пирамиды
A	B	C	D
	(2,-3, 1)	(6, 1, -1)	(4, 8, -9)	(2, -1, 2)
	(5, -1, -4)	(9, 3, -6)	(7, 10, -14)	(5, 1, -3)
	(1, -4, 0)	(5, 0, -2)	(3, 7, -10)	(1, -2, 1)
	(-3, -6, 2)	(1, -2, 0)	(-1, 5, -8)	(-3, -4, 3)
	(-1, 1, -5)	(3, 5, -7)	(1, 12, -15)	(-1, 3, -4)
	(-4, 2, -1)	(0, 6, -3)	(-2, 13, -11)	(-4, 4, 0)
	(0, 4, 3)	(4, 8,1)	(2, 15, -7)	(0, 6, 4)
	(-2, 0, –2)	(2, 4, -4)	(0, 11, -12)	(-2, 2, –1)
	(3, 3, -3)	(7, 7, -5)	(5, 14, -13)	(3, 5, -2)
	(4, -2, 5)	(8, 2, 3)	(6, 9, -5)	(4, 0, 6)

Задача 4. Даны координаты вершин треугольника ABC. Сделать чертеж в системе координат. Найти:

1) длину стороны AB;

2) уравнения сторон AB и BC;

3) уравнение высоты CD и ее длину;

4) уравнение прямой, проходящей через точку С параллельно стороне AB.

№ варианта	Вершина А	Вершина В	Вершина С
	(-9; 6)	(3; -3)	(7; 19)
	(1; 0)	(13; -9)	(17; 13)
	(-4; 10)	(8; 1)	(12; 23)
	(2; 5)	(14; -4)	(18; 18)
	(-6; 8)	(6; -1)	(4; 13)
	(-4; 12)	(8; 3)	(6; 17)
	(4; 1)	(16; -8)	(14; 6)
	(-7; 4)	(5; -5)	(3; 9)
	(0; 3)	(12; -6)	(10; 8)
	(-5; 9)	(7; 0)	(5; 14)

Задача 5.Даны координаты вершин треугольника ABC и точки M. Найти:

1) уравнение плоскости Q, проходящей через точки A, B и C;

2) каноническое уравнение прямой, проходящей через точку M перпендикулярно плоскости Q;

3) расстояние от точки M до плоскости Q.

№ вар.	Координаты точек
A	B	C	M
	(-3; -2; -4)	(-4; 2; –7)	(5; 0; 3)	(-1; 3; 0)
	(2; -2; 1)	(-3; 0; -5)	(0; -2; -1)	(-3; 4; 2)
	(5; 4; 1)	(1; 2; -2)	(3; -2; 2)	(-5; 5; 4)
	(3; 6; -2)	(0; 2; -3)	(1; -2; 0)	(-7; 6; 6)
	(1; -4; 1)	(4; 4; 0)	(-1; 2; -4)	(-9; 7; 8)
	(4; 6; -1)	(7; 2; 4)	(-2; 0; -4)	(3; 1; -4)
	(0; 6; -5)	(8; 2; 5)	(2; 6; -3)	(5; 0; -6)
	(-2; 4; -6)	(0; -6; 1)	(4; 2; 1)	(7; -1; -8)
	(–4; -2; -5)	(1; 8; –5)	(0; 4; -4)	(9; -2; –10)
	(3; 4; -1)	(2; -4; 2)	(5; 6; 0)	(11; -3; -12)

ЧАСТЬ 1. Контрольная работа № 2.

Задача 6. Найти указанные пределы.

1.а)	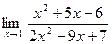;	б)	.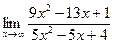
2.а)	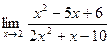;	б)	.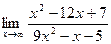
3.а)	;		.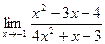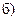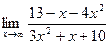
4.а)	;	)	.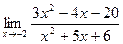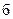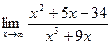
5.а)	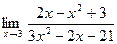;	б)	.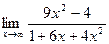
6.а)	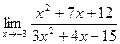;	б)	.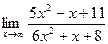
7.а)	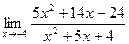;	б)	.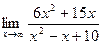
8.а)	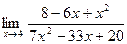;	б)	.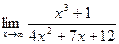
9.а)	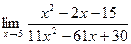;	б)	.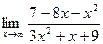
10.а)	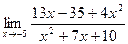;	б)	.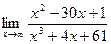

Задача 8. Найти производные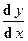

1. а)		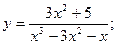	6. а)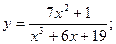
б)		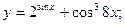	б)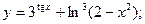
в)		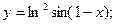	в)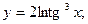
г)		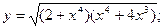	г)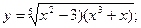
2. a)		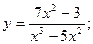	7. а)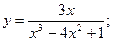
б)		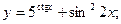	б)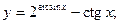
в)		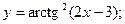	в)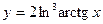
г)		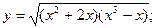	г)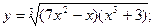
3. а)		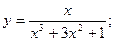	8. а)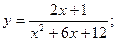
б)		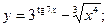	б)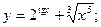
в)		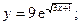	в)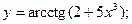
г)		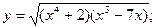	г)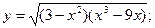
4. а)		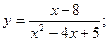	9. а)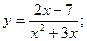
б)		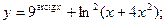	б)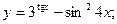
в)		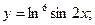	в)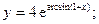
г)		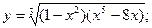	г)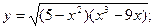
5. а)		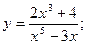	10. а)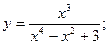
б)		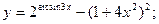	б)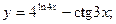
в)		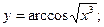	в)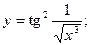
г)		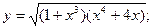	г)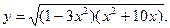

Задача 9. Исследовать функцию методами дифференциального исчисления и начертить ее график. Исследование рекомендуется проводить по следующей схеме:

1. Найти область определения.

2. Выяснить, является ли данная функция четной или нечетной.

3. Установить точки пересечения графика с осями координат.

4. Исследовать функцию на непрерывность; найти точки разрыва и ее односторонние пределы в точках разрыва.

5. Установить наличие вертикальных асимптот. Найти наклонные

(в частности горизонтальные) асимптоты.

6. Найти интервалы монотонности и точки экстремума.

7. Установить интервалы выпуклости-вогнутости и точки перегиба графика функции.

Построить график функции, используя результаты исследования. При необходимости можно дополнительно находить точки графика, давая аргументу х ряд значений и вычисляя соответствующие значения функции y.

1.	б) 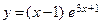.	6.	б) .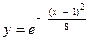
2.	б) 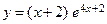.	7.	б) .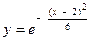
3.	б) 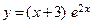.	8.	б) .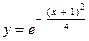
4.	б) 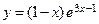.	9.	б) .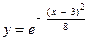
5.	б) 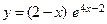.	10.	б) .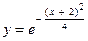

ЧАСТЬ 2. Контрольная работа № 1.

Задача 11. Исследовать функцию 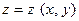на экстремум.

1.	.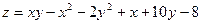
2.	.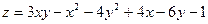
3.	.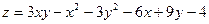
4.	.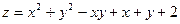
5.	.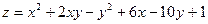
6.	.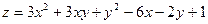
7.	.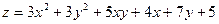
8.	.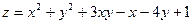
9.	.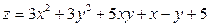
10.	.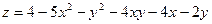

Задача 13. Даны функция 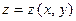, точка 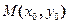и вектор 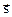. Найти grad z в точке M и производную от функции z в точке M по направлению вектора .

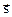1.		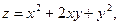M(1;1),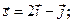
2.		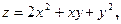M(2;1),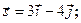
3.		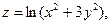M(1;1),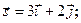
4.		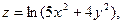M(1;1),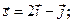
5.		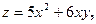M(2;1),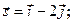
6.		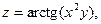M(1;2),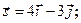
7.		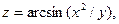M(1;2),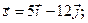
8.		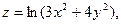M(1;3),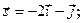
9.		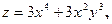M(-1;2),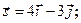
10.		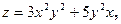M(1;1),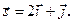

Задача 14. Найти неопределенные и вычислить указанные определенные интегралы. В п. а) результат проверить дифференцированием.

1.	а) 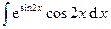:	б) .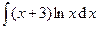
2.	а) 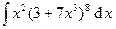;	б) .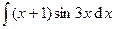
3.	а)	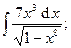б) .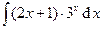
4.	а)	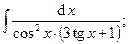б) .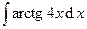
5.	а)	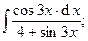б) .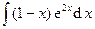
6.	а) 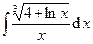;	б) .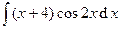
7.	а)	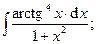б) .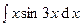
8.	а) 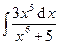;	б) .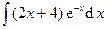
9.	а)	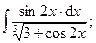б) .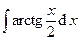
10.	а)	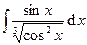б) .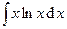

ЧАСТЬ 2. Контрольная работа № 2.

Задача 15.Вычислить определенные интегралы.

1.	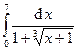.	6.	.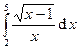
2.	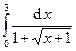.	7.	.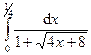
3.	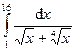.	8.	.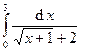
4.	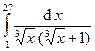.	9.	.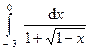
5.	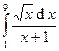.	10.	.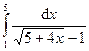

Задача 16.Вычислить несобственные интегралы или доказать их расходимость.

1.	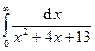.	6.	.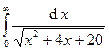
2.	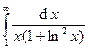.	7.	.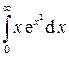
3.	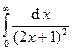.	8.	.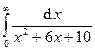
4.	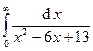.	9.	.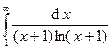
5.	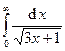.	10.	.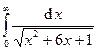

Задача 17.Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям у(0)=у₀.

1.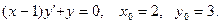
2.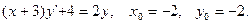
3.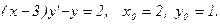
4.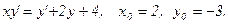
5.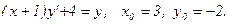
6.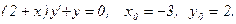
7.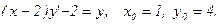
8.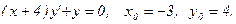
9.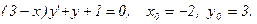
10.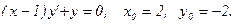

Задача 19. Найти интервал сходимости степенного ряда.

1.		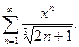6.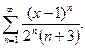
2.		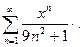7.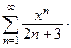
3.		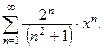8.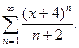
4.		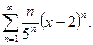9.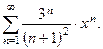
5.		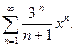10.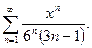