Задание 2. аппроксимация функций
Цель работы: изучить правила составления программ на языке Си, реализующих основные алгоритмы аппроксимации .функций. Освоить методику построения и использования алгебраических интерполяционных многочленов Лагранжа и Ньютона
Краткие теоретические сведения
Нахождение функции y=j(x), близкой (т.е. аппроксимирующей) к некоторой исходной функции y=f(x)является одной из основных задач теории аппроксимации функций.
Интерполяция является одним из способов аппроксимации функций. Суть ее состоит в следующем. В области значений x, представляющей некоторый интервал [a, b], где функции f и j должны быть близки, выбирают упорядоченную систему точек (узлов).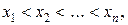 
(обозначим их как вектор 
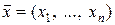), число которых равно количеству искомых параметров 
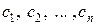. Далее, параметры вектора 
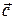подбирают такими, чтобы функция 
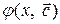совпадала с f(x) в этих узлах, 
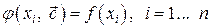(2.1)
Наиболее простой, хорошо изученной и нашедшей широкое применение в настоящее время, является линейная аппроксимация, при которой выбирают функцию 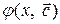, линейно зависящую от параметров .
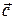Для большинства практически важных приложений при интерполяции наиболее удобны обычные алгебраические многочлены, ибо они легко обрабатываются на ЭВМ.
Из математического анализа известно, что в силу теоремы Вейерштрасса, любую функцию можно с какой угодно точностью приблизить многочленом.
Пусть f(x) – функция, непрерывная на отрезке [a,b].
Выберем на этом отрезке узлы интерполяции:
.
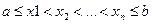Предположим, что в узлах интерполяции значения функции известны:
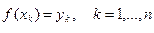. (2.2)
Ставится задача: найти алгебраический многочлен Pn-1(x) такой, что
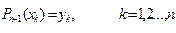. (2.3)
Интерполяционным многочленом называют алгебраический многочлен степени n-1, совпадающий с аппроксимируемой функцией в выбранных n точках.
Общий вид алгебраического многочлена
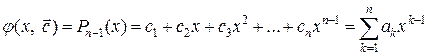(2.4)
Можно показать, что задача интерполяции посредством алгебраических многочленов имеет решение, причем единственное,
Оценка погрешности интерполяции:
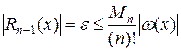, где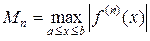 
. (2.5)
Интерполяционный многочлен Лагранжа
Многочлен Лагранжа имеет вид: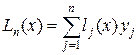 
где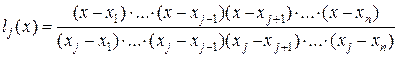 
(2.6.)
Очевидно, что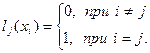 
а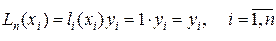 
,(2.7)
Линейная интерполяция
В общем случае для приближенного вычисления значения функции f в точке xТ находят в таблице ближайший к этой точке i-узел из общей таблицы, строят интерполяционный линейный многочлен вида:
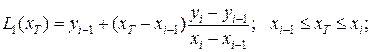(2.8)
и за значение f(x) принимают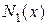 
(линейная интерполяция)
Можно показать, что погрешность линейной интерполяции оценивается как: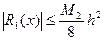 
где h – расстояние между соседними точками.