Кафедра вычислительной математики и программирования

Курсовая работа по дисциплине
Вычислительная математика

Выполнил: студент группы ИТ0951 ЗОТФ М.Г. Рымар
Проверила: А.П. Гловацкая

(Вариант №22)

Москва 2012

1. МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Задание
Решить уравнение методами итерации, Ньютона, хорд. Составить схему алгоритма уточнения корня. Получить решение по программе на языке Quick Basic. Провести оценку погрешности результата.

Исследование задания
1) Отделение корней можно провести аналитическим и графическим способами.
При графическом способе отделения корней следует построить графики функций и , затем определить отрезок, содержащий точку пересечения графиков (Рис. 1)

– отрезок изоляции.

Рис.1

Обратимся к аналитическому способу отделения корней. Определим знаки функции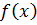

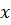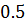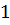На отрезке функция 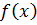меняет знак, следовательно, на отрезке существует хотя бы один корень уравнения. Убедимся, что корень единственный.

Так как , то на отрезке существует, по меньшей мере, один корень уравнения. Убедимся, что корень единственный.

Для любого 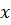из отрезка , .

Так как и на отрезке функции и сохраняют знаки, то уравнение имеет единственный корень, принадлежащий отрезку .

2) При уточнении корня методом итерации приводят уравнение к виду . Для сходимости процесса итерации необходимо, чтобы , . Укажем приём получения функции , если условие сходимости не выполнено.
Построим функцию , – некоторый параметр. Если
, то , если , то , . Такой выбор параметра позволяет обеспечить выполнение условий сходимости. Начальное значение в методе итерации – произвольное значение на отрезке .
Рекуррентная формула метода итерации .
Погрешность результата, вычисленного методом итерации, оценивается по формуле:
, , .
Воспользуемся указанным правилом выбора параметра .
, следовательно, , . Полагаем .
Пусть - начальное значение. Рекуррентная формула .
Таким образом, ( )+ , .
Выполним три итерации.
Воспользуемся программными средствами для решения уравнения методом итерации.

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1 Function f(ByVal x As Single) f = Sqrt(x + 1) - (1 / x) End Function Function fi(ByVal x As Single) fi = -0.21 * (Sqrt(x + 1) - (1 / x)) + x End Function Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function     Sub iterac(ByVal x As Single, ByRef eps As Single, ByRef L As ListBox) Dim t, f1, f2 As Single Dim z As String = "" Dim n As Integer n = 0 t = x   Do x = t z = CStr(n) + Space(6) z = z + Format(x, "0.000000") _ + Space(3) + Format(f(x), "0.0000000") L.Items.Add(z)   t = fi(x)   f1 = f(x) f2 = f(t) n = n + 1 Loop Until Abs(x - t) < eps And Abs(f1 - f2) < eps   End Sub   Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim x, eps As Single   x = vvod(TextBox1) eps = vvod(TextBox2) iterac(x, eps, ListBox1)   End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click Close() End Sub   Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click ListBox1.Items.Clear() TextBox1.Clear() TextBox2.Clear()   End Sub End Class

Оценим погрешность результата, вычисленного методом итерации.
, , .

При , .

3) Рекуррентная формула уточнения корня методом Ньютона-Рафсона
, .

Достаточные условия сходимости метода:
a) , б) и непрерывны, знакопостоянны и отличны от нуля на отрезке .

Начальное значение для метода Ньютона-Рафсона выбирается из условия

.
Оценка погрешности метода Ньютона-Рафсона:
, – наибольшее значение ,

– наименьшее значение на отрезке .

Проверим выполнение достаточных условий сходимости метода для рассматриваемого уравнения.
Выше был определён отрезок , где выполнены условия
а) , б) и знакопостоянны и отличны от нуля.
Из условия выбирается начальное значение .

Рекуррентная расчётная формула:
,
Воспользуемся программными средствами для решения уравнения методом Ньютона-Рафсона.

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1 Function f(ByVal x As Single) f = Sqrt(x + 1) - (1 / x) End Function Function fp(ByVal x As Single) fp = (1 / x ^ 2) + (1 / (2 * Sqrt(x + 1))) End Function Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function Sub vivod(ByVal x As Single, ByVal T As TextBox) T.Text = CStr(x) End Sub Sub vivodint(ByVal x As Integer, ByVal T As TextBox)   T.Text = CStr(x) End Sub Sub newt(ByRef x As Single, ByVal eps As Single, _ ByRef n As Integer, ByRef m1 As Single, ByRef L As ListBox) Dim t, f1, f2 As Single Dim z As String = "" Do z = CStr(n) + Space(10) + Format(x, "0.000000") + Space(6) + Format(f(x), "0.00000") L.Items.Add(z)   n = n + 1 t = f(x) / fp(x) f1 = f(x) x = x - t f2 = f(x)   Loop Until Abs(f2) / m1 < eps   z = CStr(n) + Space(10) + Format(x, "0.000000") + Space(6) + Format(f(x), "0.00000") L.Items.Add(z) End Sub Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim x, eps, m1 As Single Dim n As Integer x = vvod(TextBox1) eps = vvod(TextBox2) m1 = vvod(TextBox3) n = 0 newt(x, eps, n, m1, ListBox1) End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub   Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click ListBox1.Items.Clear() TextBox1.Clear() TextBox2.Clear() TextBox3.Clear() End Sub End Class

Оценим погрешность второго приближения.
. .

, .

4) Уточнение корня методом хорд. Рекуррентные формулы имеют вид:
- в случае, если неподвижна точка : ,

, .

- в случае, если неподвижна точка : ,
, .

Неподвижен тот конец отрезка , для которого знак функции совпадает со знаком её второй производной. Для сходимости метода необходимо знакопостоянство на отрезке .

Оценку погрешности можно проводить по любой из формул:
или ,

и - наименьшее и наибольшее значения на отрезке.
Выше было показано, что на отрезке . Неподвижной точкой является , так как . Таким образом, полагая , получим сходящуюся последовательность приближений к корню по формуле:
. Результаты решения методом хорд, выполненные с помощью программных средств .

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1 Function f(ByVal x As Single) f = Sqrt(x + 1) - (1 / x) End Function   Function vvod(ByVal T As TextBox) Return CSng(Val(T.Text)) End Function   Sub hord(ByVal x0 As Single, ByVal m1 As Single, ByVal a As Single, ByVal b As Single, ByVal eps As Single, ByRef L As ListBox) Dim x, c, Fc As Single Dim n As Integer Dim z As String = "" x = x0 'x = 0.5 n = 0 If x0 = a Then c = b ' c = 1.5 Else c = a End If   Fc = f(c) ' Fc=F(1.5)   z = CStr(n) + Space(6) z = z + Format(c, "0.000000") _ + Space(3) + Format(Fc, "0.0000000") L.Items.Add(z) x = c ' x = 1.5 Do n = n + 1 ' n = 1 x = x - (f(x) / (f(x) - f(a))) * (x - a)   z = CStr(n) + Space(6) z = z + Format(x, "0.000000") _ + Space(3) + Format(f(x), "0.0000000") L.Items.Add(z)   Loop Until Abs(f(x) / m1) < eps   End Sub   Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim x0, a, b, m1, eps As Single x0 = vvod(TextBox1) a = vvod(TextBox2) b = vvod(TextBox4) m1 = vvod(TextBox3) eps = vvod(TextBox5) hord(x0, m1, a, b, eps, ListBox1) End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click End End Sub   Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click ListBox1.Items.Clear() TextBox1.Clear() TextBox2.Clear() TextBox3.Clear() TextBox4.Clear() TextBox5.Clear() End Sub End Class

Погрешность для третьей итерации: , .
Погрешность для четвёртой итерации: , .

ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ

Задание
Выполнить линейную и квадратичную интерполяцию таблично заданной функции .

Вычислить значение интерполирующей функции в точках и . Оценить погрешность интерполяции.

Исследование задания
Шаг таблицы постоянный, поэтому можно построить интерполяционный многочлен Ньютона
, .

Ближайший к точке узел справа – , поэтому полагаем . Для линейной интерполяции следует взять узлы , . Для квадратичной интерполяции последовательность узлов , , (число узлов равно , где – порядок интерполирующего многочлена).

Погрешность можно оценить по формуле: .

Получим таблицу конечных разностей .

1. Построим и вычислим .

, . При и

.

Построим и вычислим .

.

.

Воспользуемся программными средствами для вычисления значений полинома первой и второй степени в точке .

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1   'Процедура вывода одномерного массива Public Sub PrintL(ByRef x() As Double, ByVal k As Integer, ByRef LB As ListBox) Dim i As Integer Dim y As String = "" For i = 1 To k y = Space(5) + CStr(i) + Space(20) + CStr(x(i)) LB.Items.Add(y) Next i End Sub 'Процедура формирования матрицы конечных разностей Sub KONRAZN(ByVal F() As Double, ByRef DY(,) As Double, ByVal n As Integer) Dim i, j As Integer For i = 0 To n DY(i, 0) = F(i) For j = 1 To n DY(i, j) = 0 Next j Next i For j = 1 To n For i = 0 To n - j DY(i, j) = DY(i + 1, j - 1) - DY(i, j - 1) Next i Next j End Sub   'Процедура родсчета значений полинома степени М Sub NEWTON2(ByVal q As Double, ByVal M As Integer, ByVal DY(,) As Double, _ ByRef p As Double, ByRef R As Double) Dim qq, fact As Double Dim k, j As Integer k = DY.GetLength(0) - 1 p = DY(k, 0) qq = 1 fact = 1 For j = 1 To M fact = fact * j qq = qq * (q + j - 1) R = qq * DY(k - j, j) / fact p = p + R Next j End Sub   Sub ReadUzlY(ByRef y() As Double, ByVal n As Integer) Dim i As Integer For i = 0 To n y(i) = CDbl(Val(RichTextBox3.Lines(i))) Next End Sub   Sub inter_po_newton2(ByVal x As Double, ByVal DY(,) As Double, ByVal xn As Double, _ ByVal h As Double, ByVal n As Integer, ByRef P() As Double, ByRef m As Integer) Dim i As Integer, eps As Double Dim q As Double, R As Double eps = CDbl(Val(TextBox1.Text)) 'точность q = (x - xn) / h i = 1 NEWTON2(q, i, DY, P(i), R) Do While Abs(R) > eps And i < n i = i + 1 NEWTON2(q, i, DY, P(i), R) Loop m = i End Sub Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click   Dim xx, xn, h As Double Dim nn, m As Integer xx = CDbl(Val(TextBox5.Text)) 'точка интерполяции nn = CInt(Val(TextBox6.Text)) 'кол-во узлов в таблице nn = nn - 1 xn = CDbl(Val(TextBox3.Text)) 'ближ. узел справа(снизу) h = CDbl(Val(TextBox4.Text)) 'шаг таблицы Dim yu(nn) As Double 'массив значений функции Dim DY(nn, nn) As Double 'матрица конечных разностей Dim P(nn) As Double 'получ. массив значений полинома ReadUzlY(yu, nn) KONRAZN(yu, DY, nn) inter_po_newton2(xx, DY, xn, h, nn, P, m) PrintL(P, m, ListBox2) End Sub   Private Sub Button4_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button4.Click ListBox2.Items.Clear()   End Sub   Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click End End Sub     End Class

Теперь, используя программу Mathcad, вычислим значение полинома второй степени во всех узлах интерполяции, а результаты запишем в таблицу ниже.

Mathcad

Таблица результатов

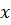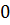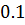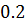Как мы видим, значение полинома второй степени в узлах интерполяции полностью совпадает с начальными условиями. Следовательно, можно сделать вывод о том, что интерполяционный полином второй степени был построен правильно.

2. Оценим погрешность интерполяции по формулам практической оценки погрешности.

.

.

3. Для данной таблицы можно построить и интерполяционный многочлен Лагранжа, т.к. формула Лагранжа универсальна.

.

Оценку погрешности определяют по формуле: .

Для обеспечения большей точности интерполяции перенумеруем узлы интерполяции:
( ближайший к точке )

Многочлен Лагранжа при .
При

Многочлен Лагранжа при

.

Воспользуемся программными средствами для построения интерполяционного многочлена второй степени в явном виде.

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1 Function Lag(ByVal x As Double, ByVal a As Double, ByVal b As Double, ByVal c As Double) As Double Lag = a * x * x - b * x + c End Function   Sub REadUzl(ByVal n As Integer, ByRef x() As Double, ByRef y() As Double) Dim i As Integer For i = 0 To n x(i) = CDbl(Val(RichTextBox1.Lines(i))) y(i) = CDbl(Val(RichTextBox2.Lines(i))) Next End Sub   Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim xx, l2 As Double Dim nn, i As Integer xx = CDbl(Val(TextBox1.Text)) 'точка интерполяции nn = CInt(Val(TextBox2.Text)) 'число узлов+1(номер последнего узла) Dim xu(nn), yu(nn), L(nn), E1(nn), a, b, c As Double REadUzl(nn, xu, yu) a = yu(0) / ((xu(0) - xu(1)) * (xu(0) - xu(2))) + yu(1) / ((xu(1) - xu(0)) * (xu(1) - xu(2))) + yu(2) / ((xu(2) - xu(0)) * (xu(2) - xu(1))) b = (xu(1) + xu(2)) * yu(0) / ((xu(0) - xu(1)) * (xu(0) - xu(2))) + (xu(0) + xu(2)) * yu(1) / ((xu(1) - xu(0)) * (xu(1) - xu(2))) + (xu(0) + xu(1)) * yu(2) / ((xu(2) - xu(0)) * (xu(2) - xu(1))) c = xu(1) * xu(2) * yu(0) / ((xu(0) - xu(1)) * (xu(0) - xu(2))) + xu(0) * xu(2) * yu(1) / ((xu(1) - xu(0)) * (xu(1) - xu(2))) + xu(0) * xu(1) * yu(2) / ((xu(2) - xu(0)) * (xu(2) - xu(1))) TextBox4.Text = CStr(a) TextBox5.Text = CStr(-b) TextBox6.Text = CStr(c) l2 = Lag(xx, a, b, c) ListBox1.Items.Add("Знач. в точке интерпол " + Format(l2, "0.00000")) ListBox1.Items.Add("Знач. в узлах интерпол ") For i = 0 To nn l2 = Lag(xu(i), a, b, c) ListBox1.Items.Add(Format(l2, "0.0000")) Next End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click ListBox1.Items.Clear() End Sub     Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click End End Sub   End Class

Воспользуемся программными средствами для вычисления , а также в целях проверки предыдущих вычислений.

Скриншот работы программы

Исходный код программы

Imports System.Math Public Class Form1   Function Lagr(ByVal x As Double, ByVal xu() As Double, ByVal yu() As Double, ByVal k As Integer) As Double Dim s, p As Double Dim i, j As Integer s = 0 For i = 0 To k p = 1 For j = 0 To k If i <> j Then p = p * (x - xu(j)) / (xu(i) - xu(j)) End If Next j s = s + p * yu(i) Next i Lagr = s End Function Sub Inter_po_Lagr(ByVal x As Double, ByVal xu() As Double, ByVal yu() As Double, _ ByVal n As Integer, ByVal eps As Double, ByRef L() As Double, ByRef k As Integer) Dim E1 As Double k = 1 L(k) = Lagr(x, xu, yu, k) Do k = k + 1 L(k) = Lagr(x, xu, yu, k) E1 = Abs(L(k) - L(k - 1)) Loop Until E1 <= eps Or k = n End Sub     Sub REadUzl(ByVal n As Integer, ByRef x() As Double, ByRef y() As Double) Dim i As Integer For i = 0 To n x(i) = CDbl(Val(RichTextBox1.Lines(i))) y(i) = CDbl(Val(RichTextBox2.Lines(i))) Next End Sub 'Процедура вывода одномерного массива Public Sub PrintL(ByRef x() As Double, ByVal k As Integer, ByRef LB As ListBox) Dim i As Integer Dim y As String = "" For i = 1 To k y = Space(5) + CStr(i) + Space(20) + CStr(x(i)) LB.Items.Add(y) Next i   End Sub Private Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click Dim eps, xx As Double Dim nn, k As Integer eps = CDbl(Val(TextBox3.Text)) 'точность xx = CDbl(Val(TextBox1.Text)) 'точка интерполяции nn = CInt(Val(TextBox2.Text)) 'число узлов+1(номер последнего узла) Dim xu(nn), yu(nn), L(nn) As Double REadUzl(nn, xu, yu) Inter_po_Lagr(xx, xu, yu, nn, eps, L, k) PrintL(L, k, ListBox1) '   End Sub   Private Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.Click ListBox1.Items.Clear() End Sub     Private Sub Button3_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button3.Click End End Sub     End Class

4. Проведём оценку погрешности.

Таблица 2

5. Результаты интерполяции сведены в таблицу 2.

Число узлов			Оценка погрешности
Метод Ньютона	Метод Лагранжа