Метод замены иррациональных уравнений системой рациональных уравнений
II. Практикум.
1. Решение простейших иррациональных уравнений, используя свойство корня n-ой степени 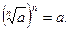
Пример 1.
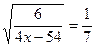
При возведении обеих (неотрицательных) частей уравнения в квадрат, получаем равносильное уравнение:
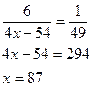
Ответ: 87.
Пример 2.
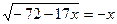
Возведем обе части уравнения в квадрат, получим уравнение-следствие:
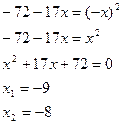
Проверка:
Если 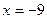 , то
, то
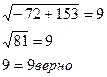
Если 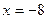 , то
, то
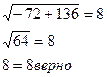
Ответ: - 9, - 8.
Метод возведения в степень.
Пример 1.
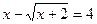
Уединим корень, после чего возведем обе части уравнения в квадрат:
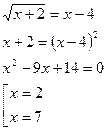
Проверка показала, что 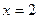 посторонний корень.
посторонний корень.
Ответ: 7.
Пример 2.
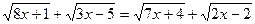
Уединим по два радикала в каждой части уравнения так, чтобы сумма подкоренных выражений была одинакова.
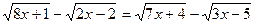
8х + 1 + 2х – 2 – 2 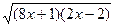 = 7х + 4 + 3х – 5 – 2
= 7х + 4 + 3х – 5 – 2 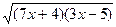
(8х + 1)(2х – 2) = (7х + 4)(3х – 5)
х = 3; х = - 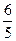
Проверка: х = - 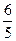 посторонний корень
посторонний корень
Ответ: 3.
Пример 3.
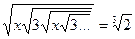
х 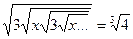
3х2 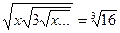 , т.к.
, т.к. 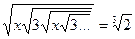 , то
, то
3х2 × 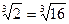
3х2 = 2
х 1 = - 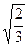 посторонний корень х2 =
посторонний корень х2 = 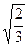
Ответ: 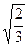 .
.
Пример 4.
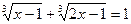
Возведем обе части уравнения в куб, используя формулу 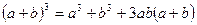
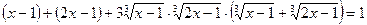
По условию 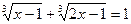 .
.
Тогда 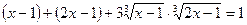
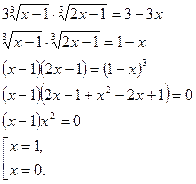
Проверка показала, что х = 0 посторонний корень.
Ответ: 1.
Пример 5.
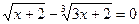
Уединим корни и возведем обе части уравнения в 6 степень (НОК(2; 3) = 6)
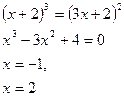
Проверка показала, что х = – 1 – посторонний корень.
Ответ: 2.
Метод введения новой переменной.
Пример 1.
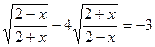
Пусть 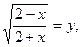 y > 0. Получим уравнение
y > 0. Получим уравнение 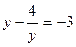 .
.
Тогда у2 + 3у – 4 = 0
у1 = 1, у2 = -4 (не удовлетворяет условию y > 0)
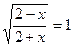
2 – х = 2 + х
х = 0
Проверка показывает, что 0 является корнем уравнения.
Ответ: 0.
Пример 2.
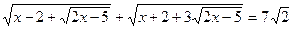
Пусть 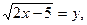
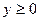
2х – 5 = у2
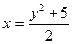
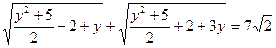
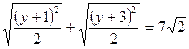 | ×
| × 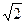
|y + 1| + |y + 3| = 14, т.к. у ³ 0, то |y + 1| = y + 1, |y + 3| = y + 3
у + 1 + у + 3 = 14
2у = 10
у = 5
Тогда х = 15.
Ответ: 15.
Пример 3.
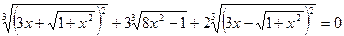
Заметим, что 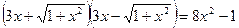 , тогда имеем
, тогда имеем
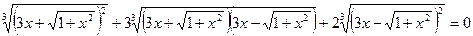
Это однородное уравнение. Разделим почленно на 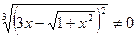
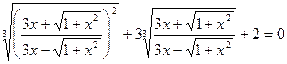
Введем новую переменную 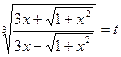 . Получим
. Получим
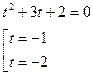
Вернувшись обратно к замене, получим: х=0, х= 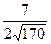 .
.
Ответ: 0; 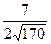 .
.
Метод составления смешанной системы.
Решение уравнений вида 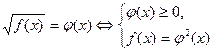
Пример 1.
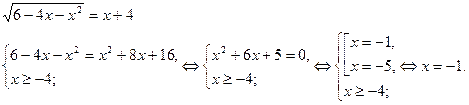
Ответ: -1.
Решение уравнений вида 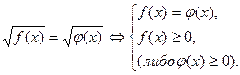
Пример 2.
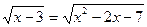
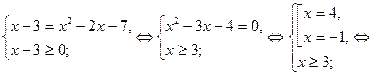 х = 4
х = 4
Ответ: 4.
Пример 3.
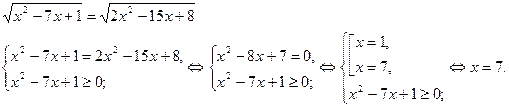
Ответ: 7.
Решение уравнений вида 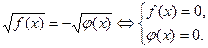
Пример 4.
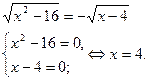
Ответ: 4.
Решение уравнений вида 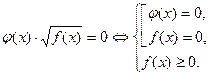
Пример 5.
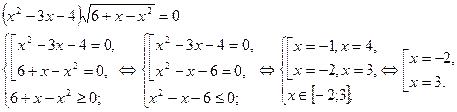
Ответ: -2; 3.
Пример 6.
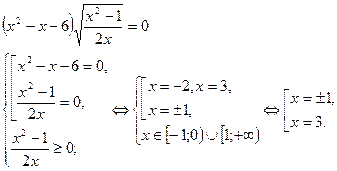
Ответ: -1; 1; 3.
Метод разложения подкоренного выражения на множители.
Пример 1.
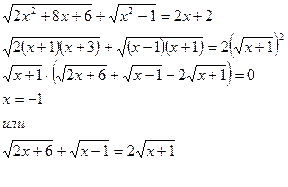
Возведем обе части уравнения в квадрат, получим:
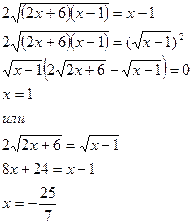
Проверка показала, что 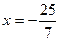 посторонний корень.
посторонний корень.
Ответ: -1; 1.
Пример 2.
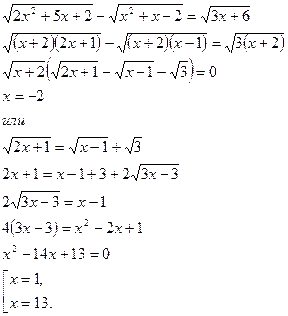
Проверка показала, что посторонних корней нет.
Ответ: -2; 1; 13.
Метод умножения на сопряженное выражение.
Пример 1.
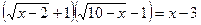
Умножим обе части уравнения на выражение 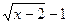 , сопряженное выражению
, сопряженное выражению 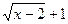 , предварительно проверив, что корень уравнения
, предварительно проверив, что корень уравнения 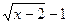 =0 х = 3 не является корнем данного уравнения.
=0 х = 3 не является корнем данного уравнения.
Получим:
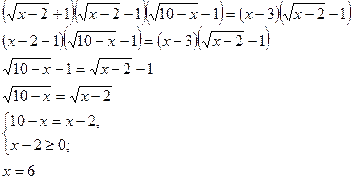
Ответ: 6.
Пример2.
(1) 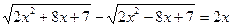 | ∙
| ∙ 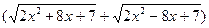
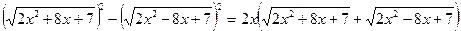
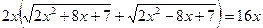
х=0 или 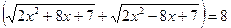
Сложим данное уравнение с уравнением (1), получим
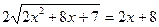
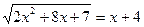
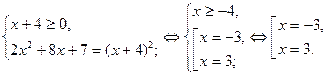
Ответ: -3; 0; 3.
Метод выделения полного квадрата в подкоренном выражении.
Пример 1.
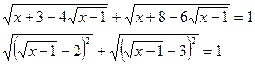
Пусть 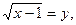
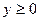
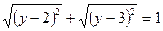
|y – 2| + |y – 3| = 1
1) 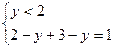 2)
2) 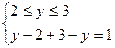 3)
3) 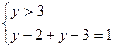
y =2 1 = 1 у = 3
решений нет 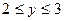 решений нет
решений нет
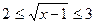
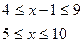
Ответ: [5; 10].
Пример 2.
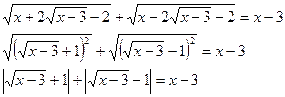
Т.к. левая часть уравнения неотрицательна, то 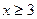 .
.
При 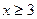
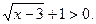 Тогда
Тогда
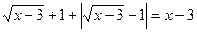
Т.к. 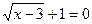 при х = 4, то рассмотрим два случая:
при х = 4, то рассмотрим два случая: 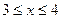 и x > 4.
и x > 4.
1 случай: 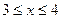
При этих значениях переменной 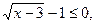 то есть уравнение равносильно системе:
то есть уравнение равносильно системе:
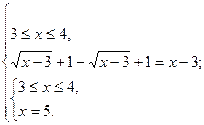
Система не имеет решения.
2 случай: x > 4.
При этих значениях переменной 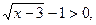 то есть уравнение равносильно системе:
то есть уравнение равносильно системе:
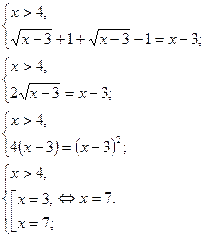
Ответ: 7.
Метод замены иррациональных уравнений системой рациональных уравнений.
Пример 1.
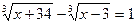
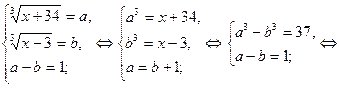
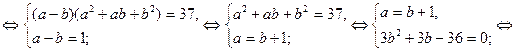
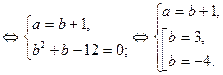
1) 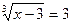 2)
2) 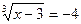
х – 3 = 27 х – 3 = -64
х = 30 х = -61
Ответ: -61; 30.
Пример 2.
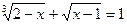
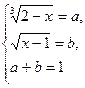
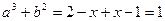
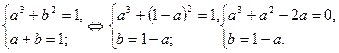
Решая первое уравнение системы, находим 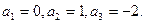
Возвращаясь к подстановке 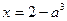 , получаем
, получаем 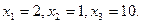
Ответ: 1; 2; 10.
