Метод замены переменной
Пример 6.
Вычислите определенный интеграл 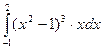 .
.
Решение.
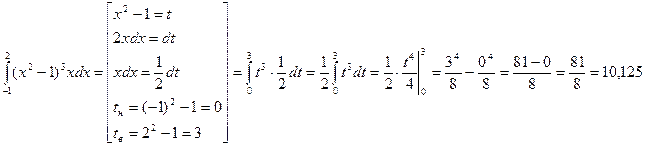
Примеры вычисления интегралов
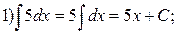
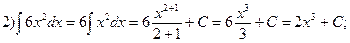
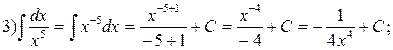
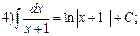
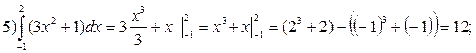
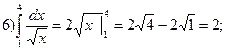
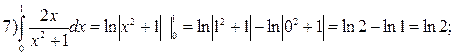
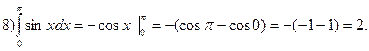
Вычисление площадей плоских фигур.
Для вычисления площадей плоских фигур применяется определенный интеграл.
Чтобы вычислить площадь плоской фигуры надо:
1) выполнить рисунок;
2) определить границы фигуры, площадь которой надо найти;
3) вычислить площадь фигуры.
Рассмотрим всевозможные случаи.
Пример 1.
Вычислите площадь фигуры, ограниченной линиями:
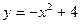 ,
, 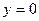 (ось х).
(ось х).
Решение.
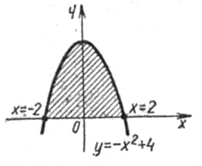
Выполним построение фигуры, ограниченной параболой 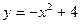 и осью Ох. Построим параболу
и осью Ох. Построим параболу 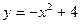 , ветви которой направлены вниз (коэффициент перед
, ветви которой направлены вниз (коэффициент перед 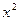 равен (-1) ). Найдем точки пересечения параболы с осью Ох. Для этого решим уравнение
равен (-1) ). Найдем точки пересечения параболы с осью Ох. Для этого решим уравнение 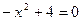 ,
,
получим 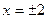 .
.
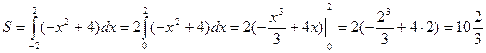 (кв.ед.)
(кв.ед.)
Границы интегрирования были уменьшены на основании свойства определенного интеграла.
Пример 2.
Вычислите площадь фигуры, ограниченной линиями:
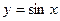 ,
, 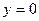 ,
, 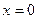 ,
, 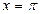 .
.
Решение.
Искомая площадь ограничена полуволной синусоидой и осью Ох.
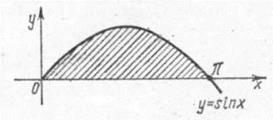
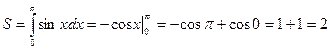 (кв.ед.)
(кв.ед.)
Пример 3.
Вычислите площадь фигуры, ограниченной линиями:
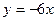 ,
, 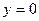 ,
, 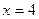 .
.
Решение.
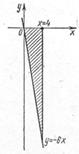
Построим прямые 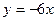 и х=4. Фигура, ограниченная указанными линиями, располагается ниже оси Ох.
и х=4. Фигура, ограниченная указанными линиями, располагается ниже оси Ох.
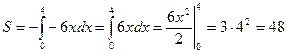 (кв.ед.)
(кв.ед.)
Пример 4.
Вычислите площадь фигуры, ограниченной линиями:
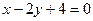 ,
, 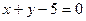 и
и 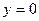 .
.
Решение.
Выполним построение фигуры. Запишем функции в привычном виде
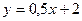 и
и 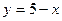 . Для них составим таблицы :
. Для них составим таблицы :
для первой
| х | -4 | |
| у |
для второй
| х | ||
| у |
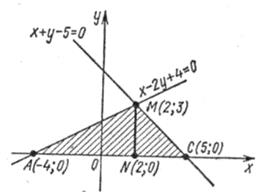
Найдем точку пересечения прямых, для этого составим и решим систему уравнений
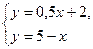
Получим х=2, у=3. На рисунке это точка М(2;3).
Искомая площадь фигуры состоит из суммы площадей двух треугольников АМN и СМN.
Вычислим площадь каждого из них и сложим полученные результаты.
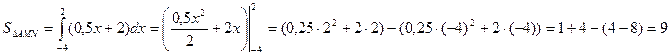
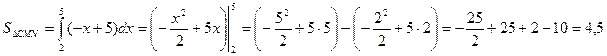 .
.
Площадь всей фигуры будет:
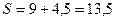 (кв.ед.)
(кв.ед.)
Пример 5.
Вычислите площадь фигуры, ограниченной линиями:
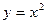 ,
, 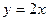 .
.
Решение.
Данная фигура ограничена параболой 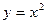 и прямой
и прямой 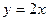 .
.
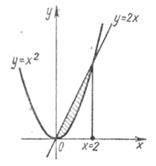
Найдем точки пересечения прямых, для этого составим и решим систему уравнений
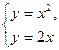
Получим х=0, х=2.
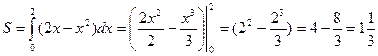 (кв.ед)
(кв.ед)
Рассмотрим еще несколько примеров решения задач:

Пример 2. Вычислить площадь плоской фигуры, ограниченной линиями: 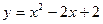 , x=-1, x=2 и осью OX.
, x=-1, x=2 и осью OX.
Решение: данная фигура представляет собой криволинейную трапецию, поэтому её площадь вычисляется по формуле (1).
 | 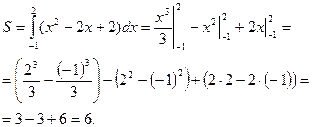 Ответ: 6 кв.ед. Ответ: 6 кв.ед. |
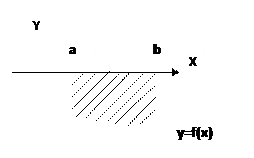
Пусть y=f(x) – непрерывная функция при x 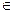 [a, b], график которой расположен ниже оси OX (рис. 3). Значение определённого интеграла будет отрицательным, поэтому для расчёта площади берём значение интеграла по модулю.
[a, b], график которой расположен ниже оси OX (рис. 3). Значение определённого интеграла будет отрицательным, поэтому для расчёта площади берём значение интеграла по модулю.
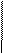     |  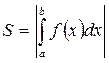 (2) (2) |
Пример 3. Вычислить площадь плоской фигуры, ограниченной графиком функции 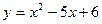 и осью OX.
и осью OX.
Решение: данная фигура расположена ниже оси OX, поэтому применим формулу.
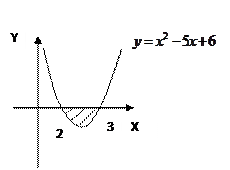 | 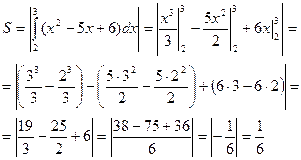 Ответ: 1/6 кв.ед. Ответ: 1/6 кв.ед. |
Пример 4. Вычислить площадь плоской фигуры, ограниченной графиками функций 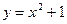 и
и 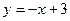 .
.
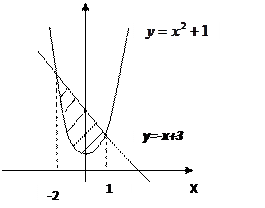 | Решение: данная фигура представляет собой разность криволинейных трапеций Абсциссы точек пересечения находим по чертежу: x1=-2 и x2=1. 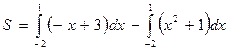 . Можно записать под один интеграл: . Можно записать под один интеграл: 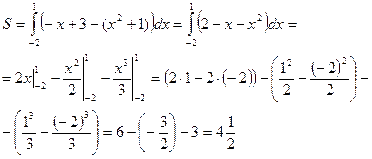 Ответ: 4,5 кв.ед. Ответ: 4,5 кв.ед. |
Пример 5. Вычислить площадь плоской фигуры, ограниченной графиками функций 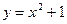 и
и 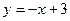 , и координатными осями.
, и координатными осями.
Решение: данная фигура представляет собой сумму криволинейных трапеций S=S1+S2, где 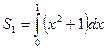 и
и 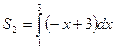 . Получим формулу:
. Получим формулу:
     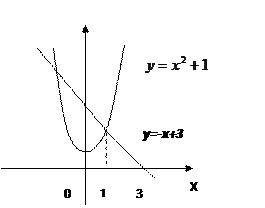 |  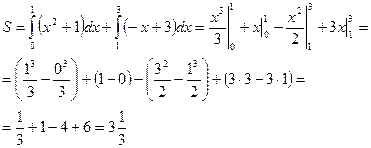 Ответ: Ответ: 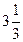 кв.ед. кв.ед. |
