Цилиндрические поверхности.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром при этом кривая К – направляющая цилиндра, а L – его образующая.

Эллиптический цилиндр

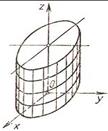Эллиптическое уравнение:

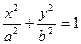
Частным случаем эллиптического цилиндра является круговой цилиндр, его уравнение x² + y² = R². Уравнение x²=2pz определяет в пространстве параболический цилиндр.

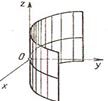
Уравнение: 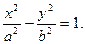определяет в пространстве гиперболический цилиндр.

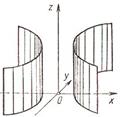
Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих координат x, y, z.

Графики в полярной системе координат и параметрически заданных функций.

Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат.

Полярная система координат.

Точка О называется полюсом, а луч l – полярной осью.

Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.

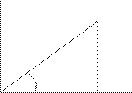
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Действительные числа.

Действительные числа образуют совокупность элементов, обладающую следующими свойствами.

Если a и b - действительные числа (алгебраические, рациональные, целые, положительные целые), то таковыми же являются и

1. a + b и ab (замкнутость),

2. a + b = b + a, ab = ba (коммутативность),

3. a + (b + c) = (a + b) + c = a + b + c, a(bc) = (ab)c = abc (ассоциативность

4. a * 1 = a (единица),

5. a(b + c) = ab + ac (дистрибутивность),

6. из a + c = b + c следует a = b, из ca = cb, , следует a = b (сокращение).

Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a.

Действительные числа, не являющиеся рациональными, называются иррациональными.

Действительными алгебраическими числами называются действительные корни алгебраических уравнений с целочисленными коэффициентами, а действительными трансцендентными числами - остальные действительные числа.