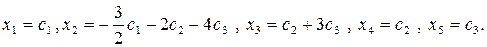Примеры для самостоятельной работы. Решить систему уравнений методами Гаусса и Жордана – Гаусса:
Решить систему уравнений методами Гаусса и Жордана – Гаусса:
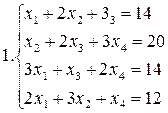
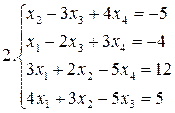
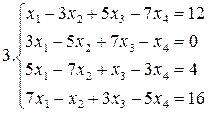
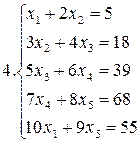
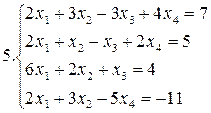
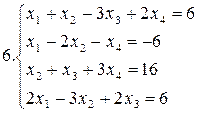
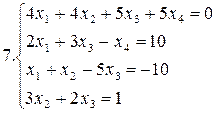
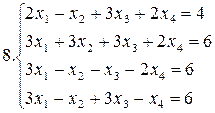
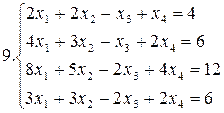 10.
10. 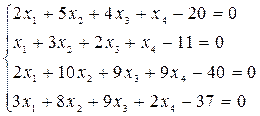
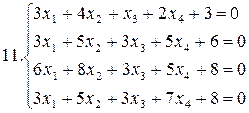
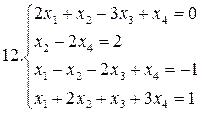
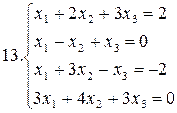
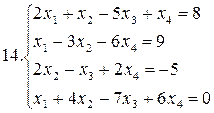
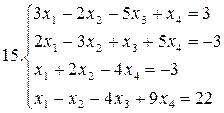
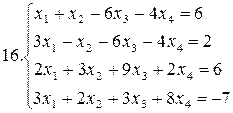
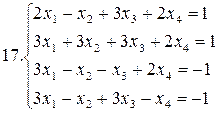
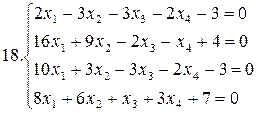
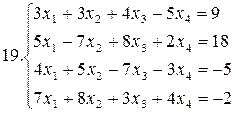
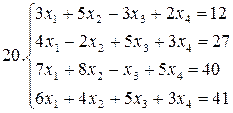
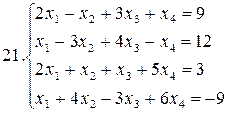
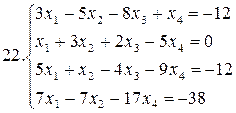
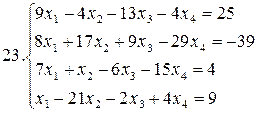
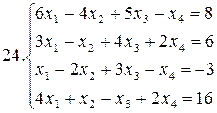
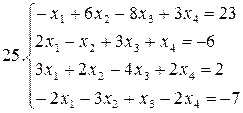 26.
26. 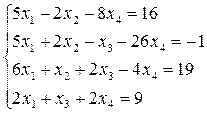
27. 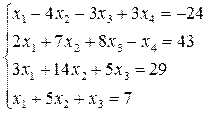 28.
28. 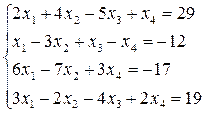
29. 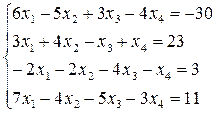 30.
30. 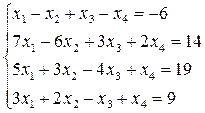
Задание № 11
Пример 15. Найти собственные значения и собственные векторы линейного преобразования с матрицей 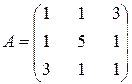 .
.
Решение. Составим характеристическое уравнение
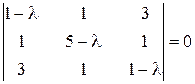 или
или
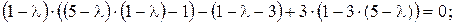
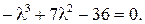
Один из корней характеристического уравнения найдем среди делителей свободного члена. Например, 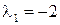 – корень данного уравнения. Разделим левую часть последнего уравнения на выражение
– корень данного уравнения. Разделим левую часть последнего уравнения на выражение 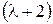 с помощью метода Горнера.
с помощью метода Горнера.
| -1 | -36 | |||
| -2 | -1 | (-2)∙(-1) + 7 = 9 | (-2)∙9 + 0 = -18 | (-2)∙(-18) – 36 = 0 |
Остальные корни характеристического уравнения определим, решив квадратное уравнение: 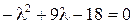 . Тогда
. Тогда 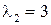 ,
, 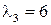 .
.
Итак, 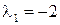 ,
, 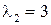 ,
, 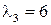 – собственные значения матрицы А.
– собственные значения матрицы А.
Вычислим собственный вектор, соответствующий собственному числу 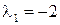 . Составим систему уравнений:
. Составим систему уравнений: 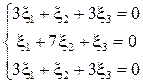 , получаем
, получаем 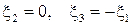 .
.
Полагаем, что 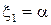 ,
, 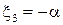 , тогда
, тогда 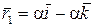 – собственный вектор, соответствующий собственному числу
– собственный вектор, соответствующий собственному числу 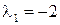 .
.
Определим собственный вектор, соответствующий собственному значению 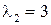 . Составим систему уравнений:
. Составим систему уравнений:
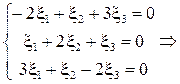
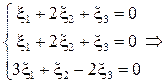
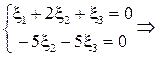
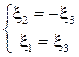 .
.
Пусть 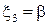 , тогда
, тогда 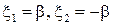 и
и 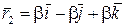 – собственный вектор, соответствующий собственному числу
– собственный вектор, соответствующий собственному числу 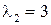 .
.
Вычислим собственный вектор, соответствующий значению 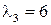 .
.
Составим систему уравнений:
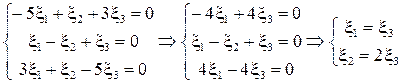 .
.
Пусть 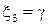 , тогда
, тогда 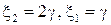 и
и 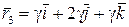 – собственный вектор, соответствующий собственному значению
– собственный вектор, соответствующий собственному значению 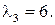
Примеры для самостоятельной работы
Найти собственные значения и собственные векторы матрицы:
1. 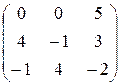 2.
2. 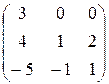 3.
3. 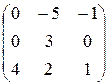
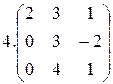
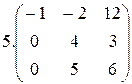
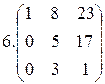
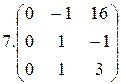
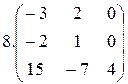
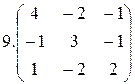
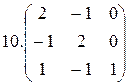
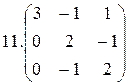
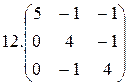
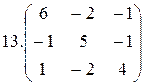
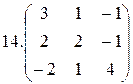
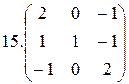
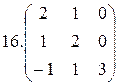
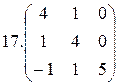
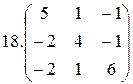
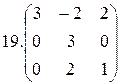
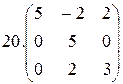
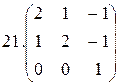
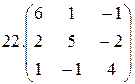
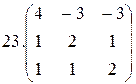
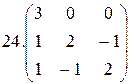
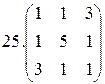 26.
26. 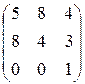 27.
27. 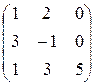
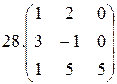
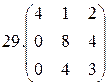
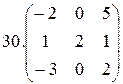
Задание № 12
Пример 16. Найти ранг системы однородных линейных уравнений, фундаментальную систему решений, общее решение:
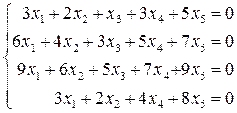 .
.
Решение.Составим матрицу системы 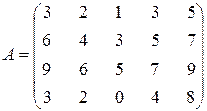 .
.
Найдём ранг матрицы А
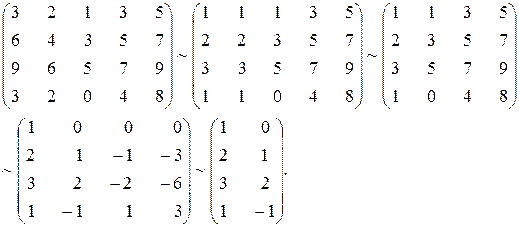
Очевидно, что r(А)=2.
Поэтому k = n – r = 5 – 2 = 3. Значит, размерность линейного пространства решений равна 3, фундаментальная система решений состоит из трёх решений.
В матрице 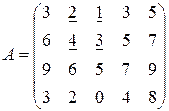 возьмем базисный минор – это
возьмем базисный минор – это
выделенный подчеркиванием минор второго порядка.
Поэтому последние два уравнения отбрасываем, а неизвестные х1, х4, х5 считаем свободными и переносим их в правую часть уравнений, то есть приходим к системе
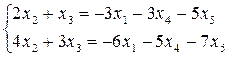 .
.
Определителем этой системы является базисный минор, который отличен от нуля. Следовательно, система имеет единственное решение, которое найдем по правилу Крамера.
Итак,
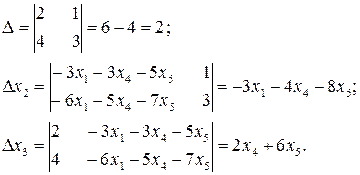
Тогда 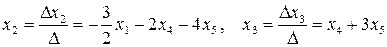 .
.
Определим первое базисное решение l1. Для этого положим x1 = 1,
x4 = x5 = 0. Тогда x2 = -3/2, x3 = 0. Таким образом, 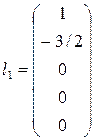 . Аналогично определим второе базисное решение
. Аналогично определим второе базисное решение 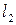 . Полагая x1 = 0, x4 = 1, x5 = 0, находим x2 = –2, x3 = 1. Второе базисное решение запишется в виде
. Полагая x1 = 0, x4 = 1, x5 = 0, находим x2 = –2, x3 = 1. Второе базисное решение запишется в виде 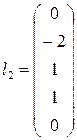 . При x1 = 0, x4 = 0, x5 = 1 определяем x2= –4, x3=3. Следовательно, третье базисное решение есть
. При x1 = 0, x4 = 0, x5 = 1 определяем x2= –4, x3=3. Следовательно, третье базисное решение есть 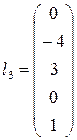 . Итак, получили фундаментальную систему решений. Отметим, что l1, l2, l3, образующие фундаментальную систему уравнений, линейно независимы, поскольку свободные неизвестные x1, x2, x3 были выбраны так, что выделенный подчёркиванием минор третьего порядка в матрице из столбцов l1, l2, l3 отличен от нуля
. Итак, получили фундаментальную систему решений. Отметим, что l1, l2, l3, образующие фундаментальную систему уравнений, линейно независимы, поскольку свободные неизвестные x1, x2, x3 были выбраны так, что выделенный подчёркиванием минор третьего порядка в матрице из столбцов l1, l2, l3 отличен от нуля 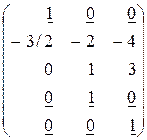 .
.
Запишем общее решение исходной системы линейных однородных уравнений: 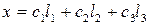 или в координатной форме
или в координатной форме
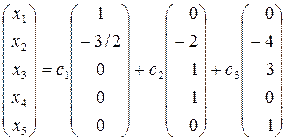 .
.
Итак,